3.4. Приближённые граничные условия
Приведём приближённые граничные условия на поверхности достаточно хорошего проводящего тела для результирующего поля в среде, окружающей это тело. Эти условия позволяют отделить решение задачи о поле в окружающей тело среде от вопроса о распределении поля в теле.
Известно, что между компонентами поля во 2-й среде существует связь:
(3.33)
Если
выполняется условие 
,
т. е. условие хорошо проводящей среды,
то волна во 2-й среде распространяется
практически перпендикулярно границе
раздела (рис. 3.6). Поэтому приближённо
можно записать
(3.34)
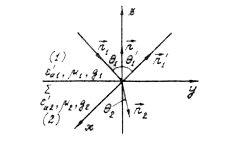
Рис.
3.6
Возьмём векторное произведение
(3.35)
Далее
применим граничные условия непрерывности
тангенциальных составляющих результирующих
векторов
и 
:
для 
,
где
– суммарное, значение вектора 
в
1-й среде; для
где
суммарное
значение вектора 
в
1-й среде.
В результате из (3.35) имеем:
(3.36)
Выражение (3.36) и представляет собой приближённые граничные условия. Эти приближённые условия впервые были указаны академиком А.Н. Щукиным. Строгое обоснование и области их применения для поверхностей любой формы было дано академиком М.А. Леонтовичем. Эти условия определяют связь между компонентами поля в 1-й среде, которая идёт через параметры 2-й среды:
.
Получим соотношения между составляющими поля в 1-й среде.
Пусть имеем поле в 1-й среде:
(3.37)
Подставив эти значения в (3.36), получим:
так
как 
.
Сравнивая соответствующие значения по координатам, имеем:
(3.38)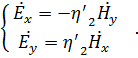
Выражения (3.38) представляют приближённые граничные условия для результирующего поля на поверхности достаточно хорошо проводящего тела.
При рассмотрении вопроса о распространении радиоволн вдоль поверхности Земли при решении задачи применяются: уравнения Максвелла для 1-й среды; уравнения Максвелла для 2-й среды; используются граничные условия, начальные условия; используются граничные условия на бесконечности (необходимо, чтобы на бесконечности решение обращалось в ноль).
Пусть
имеем плоскую границу раздела (воздух
– земля). Источник расположен на
достаточно большом расстоянии от
приёмника, т. е. волну в точке приёма
можно считать плоской. Полагаем также,
что известна вертикальная составляющая
в точке приёма. Она рассчитывается по
соответствующим формулам, например, по
формуле Шулейкина. Наша задача, определить
структуру поля в месте расположения
приёмника как над землей, так и под
землей.
Рассмотрим поле в 1-й среде, а затем применим приближенные граничные условия М.А. Леонтовича.
Так как волна по предположению плоская, то можем записать для волны типа «Т»:
(3.39)
Отсюда
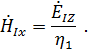
Согласно приближённым граничным условиям
(3.40)
При
этом предполагается, что
.
Учитывая, что
,
получаем
т.
е. продольная составляющая 
очень мала по сравнению с вертикальной
составляющей
(рис.
3.7).
Волна
получается эллиптически – поляризованной
(эллипс сильно вытянут). Приближённо
эту волну считают линейно-поляризованной
с углом наклона – 
,
причём
,
Р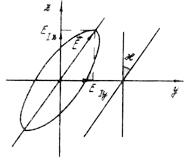
ассмотрим
вектор
во 2-й среде.
Рис.
3.7
Согласно
граничным условиям для тангенциальных
составляющих вектора
имеем:
Для
нормальных составляющих вектора 
(при
)
.
Следовательно,
(3.41)
.
Так как
,
то 
.
т. е. вертикальная составляющая во 2-й среде значительно меньше вертикальной составляющей в 1-й среде.
Установим связь между вертикальной и горизонтальной составляющими во 2-й среде.
Известно, что
(3.42)
Но
(граничные
условия для тангенциальных компонент),
поэтому из (3.41)
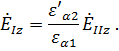
Тогда
(3.43)
,
т. е.
,
так как
Следовательно, вертикальная составляющая вектора во 2-й среде значительно меньше по модулю горизонтальной составляющей.
Таким образом, чтобы наиболее эффективно принимать поле во 2-й среде, например, в земле, которое создано в 1-й среде, необходимо использовать антенну с горизонтальной поляризацией, в то время как над землёй необходимо использовать антенну с вертикальной поляризацией.
Приближённые граничные условия применяются, когда выполняется условие. В свою очередь, это условие будет выполняться
,
при
.