Вопросы к главе 2

1. Какая электромагнитная волна называется плоской?

2. Общее решение, соответствующее плоской однородной волне.

3. Плоская электромагнитная волна в непоглощающей однородной среде.

4. Энергия, переносимая плоской электромагнитной волной в свободном пространстве.

5. Плоская волна в поглощающей среде.

6. Плоская волна в слабо поглощающей среде .

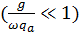7. Плоская волна в сильно поглощающей среде .

Глава 3 отражение и преломление плоских электромагнитных волн на плоской границе раздела

3.1. Направления отражённой и преломлённой волн

Пусть имеем неограниченную плоскость раздела двух сред (рис. 3.1): 1-я с параметрами , , ; 2-я – с параметрами , , ; – угол падения; – угол преломления; , , – единичные векторы.

Рис. 3.1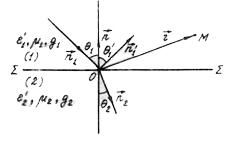

Пусть в 1-й среде распространяется плоская электромагнитная волна в направлении единичного вектора . Какое же поле будет в 1-й среде и какое – во 2-й?

Известно, что при наличии границы раздела необходимо, чтобы на этой границе удовлетворялись соответствующие граничные условия. Чтобы граничные условия удовлетворялись, следует предположить, что по обе стороны от границы раздела возникают дополнительные поля: дополнительное поле, возникающее в 1-й среде, называется отражённой волной; дополнительное поле, возникающее во 2-й среде, называется преломлённой волной.

Естественно сделать предположение: если падающая волна плоская, то отражённая и преломлённая волны так же плоские.

При этом, ввиду линейности уравнений Максвелла, будет справедлив принцип суперпозиции (наложения). Решения будут состоять из суммы решений. Чтобы граничные условия не зависели от времени, необходимо принять частоты всех волн одинаковыми. Предположив, что все волны плоские, можем записать уже известные нам решения уравнений Максвелла (2.5).

Падающая волна:

; ; ; ;

(3.1)

; ;

Отражённая волна:	Преломленная волна:
;

(3.2)

.

Уравнения (3.1) и (3.2) удовлетворяют уравнениям Максвелла. Но, ввиду наличия границы раздела, эти решения должны удовлетворять и граничным условиям.

Запишем граничные условия задачи:

а) условие непрерывности нормальных составляющих векторов

б) условие непрерывности нормальных составляющих вектора

в) условие непрерывности тангенциальных составляющих вектора

г) условие непрерывности тангенциальных составляющих вектора

Граничные условия должны выполняться в любой точке поверхности раздела. Для того чтобы данные граничные условия не зависели от того, на каком расстоянии лежит точка на поверхности от начала отсчёта (от точки 0), необходимо чтобы показательные множители выпали из данных условий. Это будет выполняться для точек поверхности раздела при условии:

(3.3)

Из (3.3) следуют два условия:

(3.4)

;

(3.5)

Анализ этих условий показывает:

1. векторы , , и лежат в одной плоскости – плоскости падения. Плоскость падения – это плоскость, содержащая векторы , и ;

2. угол падения равен углу отражения, т. е. ;

3. в

   (3.6)

   ыполняется равенство (закон синусов углов падения и преломления, или, иначе закон Снелля):

.

Так как

и

то из (3.6) следует

(3.7)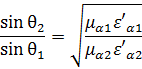

^.

В случае непоглощающих сред ( ), которые в оптике называются идеально прозрачными, получаем:

(3.8)

; ,

где и – фазовые скорости распространения;

– относительный показатель преломления.

Для диэлектриков , так как для них .