2.2. Плоская волна в непоглощающей однородной среде

Непоглощающая среда (идеальный диэлектрик) характеризуется тем, что для нее – числа чисто вещественные. Практически это допущение с большой степенью точности выполняется, например, при распространении радиоволн в воздухе, токи проводимости в котором очень малы [2].

Рассмотрим прямую волну, т. е. .

При этом – величина чисто вещественная и называется волновым сопротивлением пространства. Например, для вакуума

и волновое сопротивление

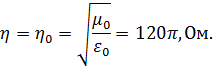
Для прямой волны

(2.6)

^,

где

Рассмотрим случай линейно-поляризованной волны. В случае линейной поляризации . Так как начальную фазу можно выбрать произвольной, то положим . Следовательно, вектор чисто вещественный. При этом нетрудно убедиться, что и будет также вещественным:

Найдём

А

(2.7)

налогично

Формулы (2.7) показывают:

1) плоская волна в неограниченной, непоглощающей среде распространяется без затухания с постоянной фазовой скоростью:

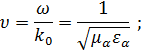
2) колебания векторов и синфазны, взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения (рис. 2.3). Вектор направлен параллельно одной и той же прямой в течение всего времени распространения, поэтому волна называется линейно-поляризованной (рис. 2.4). Векторы и изменяются по закону косинуса:

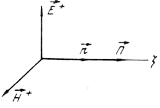
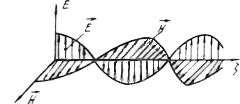
Рис. 2.4

Рис. 2.3

3) вместе с волной распространяется и электромагнитная энергия. Поток этой энергии определяется вектором Умова – Пойнтинга:

(2.8)

Мгновенное же значение вектора Умова – Пойнтинга определится выражением:

(2.9)

Из выражений (2.8) и (2.9) видно, что направление распространения энергии совпадает с направлением распространения волны и с удвоенной частотой (так как ), как показано на рис. 2.3.

В соответствии с определением вектора Умова – Пойнтинга получаем:

(2.10)

,

где – скорость распространения волны;

– объёмная плотность энергии.

Из (2.10) можно найти скорость распространения волны, если известны и :

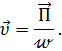
Из приведённых соотношений видно, что

(2.11)

где – волновое сопротивление пространства.

Для получения обратной волны следует лишь в формулах (2.7) изменить знаки перед и перед на противоположные, что даёт волну, которая распространяется в отрицательном направлении прямой также с постоянной амплитудой и той же фазовой скоростью, при этом

(2.12)

2.3. Плоская волна в поглощающей среде

Ограничимся рассмотрением прямой волны (для простоты письма индекс "+" опустим). В этом случае ,

кроме того, .

Рассмотрим линейно-поляризованную волну. При этом

(2.13)

,

причём , ,

Положим , тогда ,

(2.14)

П

(2.15)

редставим в виде тогда вектор определится:

где – коэффициент затухания.

Выражения (2.14) и (2.15) показывают:

1. распространяющаяся в поглощающей среде плоская волна затухает по экспоненциальному закону;

2. векторы и взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения волны;

3. волна распространяется с постоянной фазовой скоростью .

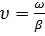Длина волны в поглощающей среде равна:

Следовательно, ;

4. в отличие от идеальной среды колебания векторов и 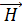во времени в поглощающей среде происходят со сдвигом фаз на угол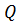 . Этот сдвиг фаз появился, вследствие того, что характеристическое сопротивление – величина комплексная.

Определим и через параметры среды и частоту:

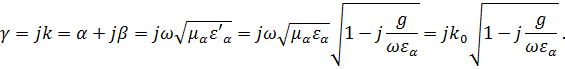
В начале определим :

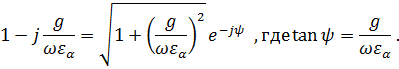
Следовательно,

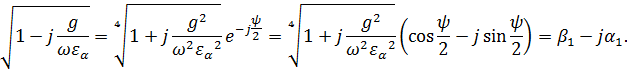
Здесь

(2.16)

;

Но

В результате

(2.17)

,

где – коэффициент затухания

– фазовый коэффициент.

.

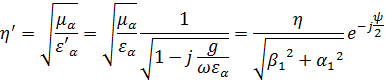С другой стороны, . Следовательно,

(2.18)

,

Из выражений (2.14) и (2.15) следует, что составляющие поля электромагнитной волны для идеальной непоглощающей среды получаются как частный случай этих выражений при . Так при получаем , , , , .

Особенностью волны, распространяющейся в поглощающей среде, является то, что основные её параметры: фазовая скорость, коэффициент затухания, характеристическое сопротивление зависят не только от параметров среды, но и от частоты. Причём зависимость эта довольно сложная, и на практике она сказывается существенно.

Так, если сигнал не является чисто гармоническим, то он, как правило, может быть представлен в виде суммы гармонических колебаний. В результате каждая гармоника будет иметь затухание, свою фазовую скорость и т. д. и поэтому при прохождении некоторого расстояния суммарный сигнал будет искажён.

Вычислим среднюю мощность потерь (потери в единицу времени и в единице объема):

(2.19)

В ычислим среднее значение вектора Умова – Пойнтинга. Этот вектор нужно знать для вычисления мощности, переносимой волной:

(2.20)

Здесь использовано известное векторное тождество

.

Рассмотрим два крайних случая.

1. .

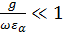В данном случае плотность тока смещения значительно больше плотности тока проводимости. Это может быть либо в слабо проводящей среде (хороший диэлектрик), либо в относительно хорошем проводнике (например, морская вода и др.), если в нём распространяются волны очень высокой частоты ( – велика).

При этом

Следовательно,

, ,

Поэтому

, ;

;

;

Получили

(2.21)

; ; .

Таким образом, в среде, где ток смещения значительно превышает ток проводимости, параметры волны от частоты не зависят. Любая гармоника распространяется с одинаковым затуханием и одинаковой фазовой скоростью, следовательно, сигнал искажаться не будет. Электромагнитный процесс здесь такой же, как и в идеальной (диэлектрической) среде, только с определенным затуханием. Само затухание может быть очень большим.

^.

Этот случай соответствует проводникам, для которых порядка См/м. В этом случае ток смещения значительно меньше тока проводимости.

При этом

^{, .}

Колебания вектора будут отставать от на :

;

.

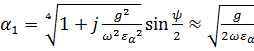Тогда

;

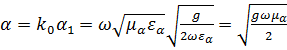(2.22)

Величина, обратная , есть скин-слой:

(2.23)

.

Найдём фазовую скорость волны:

(2.24)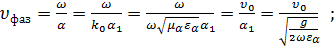

Или .

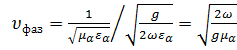Из (2.24) видим, что .

Таким образом, в данном случае основные параметры распро­страняющейся волны будут функциями частоты. Фазовая скорость при этом значительно меньше скорости света в диэлектрической среде с такими же , . Следовательно, при той же частоте длина волны в такой проводящей среде будет короче, чем в диэлектрике с параметрами , , так ,