Аналитическое условие равновесия.
При равновесии системы сил модуль равнодействующей R = [Rх2 + Rу2]1/2 = 0, поэтому Rх = Fkх = 0, Rу = Fky = 0.
Условие равновесия в аналитической форме. Для равновесия системы сходящихся сил необходимо и достаточно равенство нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей.
Д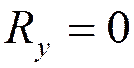
оказательство
условия равновесия в аналитической
форме. Из теоремы о существовании
равнодействующей условие равновесия
эквивалентно равенству
.
Т
о
есть
И
ли
Эти равенства позволяют определять неизвестные величины, в частности реакции связей.
З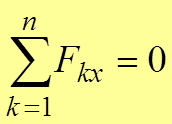
адача
статики о равновесии называется
статически определимой, если число
неизвестных не превышает числа уравнений.
Иначе задача статически неопределима
и для ее решения используются методы,
учитывающие деформацию тел. Для плоской
системы сходящихся сил число независимых
уравнений равновесия равно двум:
.
Аналитические условия равновесия представляют собой покоординатную запись векторного равенства (1):
Из равенств (2) следует, что для равновесия сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси были равны нулю.
Если сходящиеся силы расположены в одной плоскости, то имеем плоскую систему сходящихся сил. Воспользуемся произволом в выборе координатных осей и выберем их так, чтобы координатные оси оказались в одной плоскости с заданными силами. Тогда третье условие в (2) будет выполняться тождественно (всегда, при любых силах). Следовательно, для плоской системы сходящихся сил имеют место только два аналитических условия равновесия:
1.Два условия равновесия плоской системы сходящихся сил остаются и при произвольном 2.выборе осей. Кажущаяся возможность составить в этом случае также и третье условие оказывается несостоятельной: третье условие будет простым следствием первых двух, то есть не будет являться независимым.
Если среди сил, удовлетворяющих условиям равновесия, имеются неизвестные силы, тогда условия равновесия служат для определения этих сил и называются уравнениями равновесия. Такими неизвестными обычно являются реакции связей: заранее мы можем указать только направления реакций, а численные значения реакций определяются в результате составления и решения уравнений равновесия.
Пример 1. Определить давление однородного шара на гладкую стенку и натяжение нити, если шарнаходится в равновесии (рис. 27, а). Вес шара Р=20 Н, угол наклона нити к вертикали . Мысленно освободим шар от наложенных связей. Для этого связи отбросим, а их действие на шар заменяем реакциями. Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т - вдоль нити от точки А к точке В. Тем самым выявляется полная система сил, приложенных к покоящемуся шару. Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. 27, б). Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме - геометрической, аналитической).
При аналитическом способе решения выбирается подходящая система координат, и уравнения равновесия составляются в форме (2) или . Выбирая оси, как показано на рис. 27, б, составляем для данной плоской системы сходящих сил два уравнения равновесия:
Решая эти уравнения, приходим к тем же значениям для неизвестных сил: , .
Отметим, что реакция N - это сила, с которой стенка действует на шар. Давление шара на стенку суть сила N, приложенная от шара к стенке. Она равна по модулю силе N, но направлена в противоположную сторону - от шара к стенке (показана штрихами на рис. 27, а).