3. Виды связей и их реакции.

Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

    Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

    Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

     Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.

     Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.

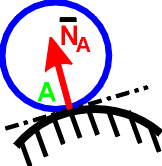
1. Гладкая плоскость (поверхность) или опора

Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.

2. Гибкая нить (провода, канаты, цепи, ремни)

Реакция Т направлена вдоль нити к точке подвеса.

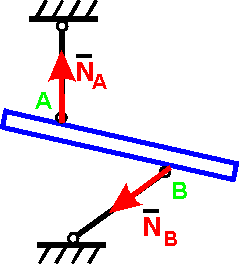
3. Невесомый стержень с шарнирами

Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.

4. Неподвижный цилиндрический шарнир илиподшипник

Реакция RA цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси в ращения, т. е. в плоскости Аху. Обычно ее раскладывают на две составляющие ХА и YA по двум взаимноперпендикулярным направлениям.

   5. Шарнирно-подвижная опора (опора на катках)

Р еакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.

4. Теорема о трех сил.

Вначале сформулируем теорему, а затем ее докажем.

Если под действием трех сил твердое тело находится в равновесии и линии действия двух сил пересекаются в одной точке, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

П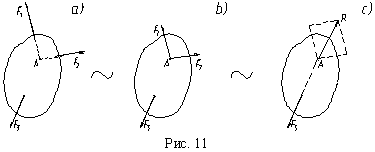 усть на твердое тело действует система трех сил F1, F2 и F3, причем линии действия первых двух пересекаются в точке A (рис. 11, a). Согласно следствию из второй аксиомы, силы F1, F2 переносим в точку A(рис. 11, b). Следуя третьей аксиоме, сложим их, заменив их одной силой, равной R=F1+F2. Таким образом, исходная система сил приведена к двум силам R и F3 (рис. 11, c).

Тело находится в равновесии. Поэтому, по первой аксиоме силы R и F3 должны иметь общую линию действия. Это может быть только тогда, когда исходные три силы лежат в одной плоскости, а линии действия сил пересекаются в одной точке. Теорема доказана.

Теорема о трех силах позволяет в ряде задач найти линию действия неизвестной силы, приложенной к твердому телу.

5. Система сходящихся сил.

Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

    Точка пересечения линий действия сил называется точкой сходимости.

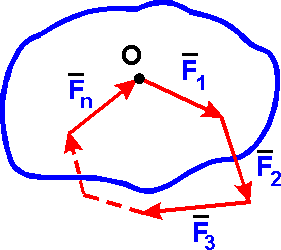
    Действие системы сходящихся сил F1, F2, ..., Fn на тело эквивалентно действию одной силы R, которая называется равнодействующей:

R = F1 + F2 + ... + Fn = Fk.     (k = 1, 2, .., n)

    Равнодействующая R приложена в точке сходимости О и является замыкающим вектором при построении силового многоугольника.

     Для равновесия твердого тела, находящегося под действием сходящейся системы сил, необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю:

R = 0,

или

F1 + F2 + ... + Fn = 0.

     Теорема о трех не непараллельных силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

    Так как  F1 + F2 +  F3 = 0, то F1 + F2 =  R12 = - F3. Cледовательно, согласно аксиоме 1 линия действия силы F3 пересекает точку О - сходимости сил F1 и F2.

Пусть, к абсолютно твердому телу приложена система N сил (F₁, F₂, ... F_N), расположенных в пространстве так, что их линии действия пересекаются в одной точке О(рисунок 1).

Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.

Приведение к равнодействующей

Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.

Рисунок 1

В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О. 

Далее, по четвертой аксиоме, силы F₁ и F₂ можно заменить их равнодействующей R_1,2(рисунок 1), которая определяется  диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.

(F₁, F₂) ~ R_1,2,

где  R_1,2=F₁+F₂.

Далее можно записать аналогичные соотношения для полученной равнодействующей силы R^*_1,2 и силы F₃, тогда

(R_1,2 F₃) ~ (F₁, F₂, F₃) ~ R_1,2,3,

где R_1,2,3=F₁+F₂+F₃      и т.д.

Для системы N сил окончательно будем иметь

(F₁ F₂ ... F_N) ~ R^*,

R^*= F₁ + F₂ + ... + F_N= ΣF_i .              (1)

На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника. 

Из конца вектора силы F₁ (точки В) проводим вектор ВС, геометрически  равный силе F₂. Из конца этого вектора (точки С) проводим вектор СD равный силе F₃. Из конца этого вектора (точки D) проводим вектор DE, равный силе F₄. 

Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называютсясоставляющими силами. Вектор АЕ, соединяющий начало А первой силы с концом Епоследней силы и направленный навстречу составляющим силам, называетсязамыкающей стороной силового многоугольника. 

Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах. 

Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.

Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.

Рисунок 2

Вычисление равнодействующей

Для аналитического определения равнодействующей найдем ее проекции R_x, R_y, R_z на оси декартовой системы координат. Имеем

R_x = Σ F_kx ,        R_y = Σ F_ky  ,       R_z = Σ F_kz .         (2)

Тогда величина равнодействующей определится следующей формулой:

или

Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:

cos α = R_x/R ,      cos β = R_y/R   ,       cos γ = R_z/R   .       (5)

Здесь  α ,  β ,  γ  - углы между положительным направлением осей координат и равнодействующей.

Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.

В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.