26. Центр тяжести твердого тела.

Центр тяжести твердого тела — точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом положении тела в пространстве. При этом поле тяжести считается однородным, т.е. силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину при любых поворотах тела. Координаты центра тяжести:

; ; , где Р=åрk, xk,yk,zk — координаты точек приложения сил тяжести рk. Центр тяжести — геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:

, DFk — элементарная площадка, F — площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то . Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a: ; кругового сектора: ; треугольник: в точке пересеч. медиан (1/3 медианы от основания).

Н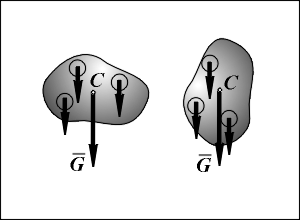 а каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести. Эти силы образуют поле силы тяжести.

Для тел, размеры которых малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполнены эти два условия, называют однородным полем тяжести.

Равнодействующая G сил тяжести, действующих на частицы данного тела, называется весом тела. По модулю вес тела равен произведению его массы m на ускорение свободного падения g  9.81 м / c² : G = m · g.

Центром тяжести тела называется неизменно связанная с этим телом точка С, через которую проходят линии действия веса тела при любом положении тела в пространстве (см.рис.).

Такая точка всегда существует и является примером так называемого центра параллельных сил.

Центр тяжести тела является геометрической точкой, которая может распологаться вне пределов данного тела (например, для кольца).

Методы определения центров тяжести плоских фигур

Примеры расположения центров тяжести плоских фигур

Центр тяжести твердого тела

Рассмотрим однородную (то есть имеющую одинаковую плотность во всех точках) тонкую фигуру (пластину), расположенную в координатной плоскости Oxy.

При определении координат x_C, y_C центра тяжести С плоской однородной фигуры применяют следующие методы:

• Для фигуры произвольной формы координаты ее центра тяжести определяются интегрированием по площади фигуры S согласно следующим формулам:

x_C = (   x dx ) / S; y_C = (   y dy ) / S.

• Если плоская однородная фигура обладает свойством симметрии, то есть имеет ось или центр симметрии, то ее центр тяжести лежит соответственно или на оси симметрии, или в центре симметрии.  Отсюда следует, что центры тяжести кольца и круглой пластины, имеющих центр симметрии, лежат в их геометрических центрах.

• Метод разбиения: если плоскую фигуру можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всей фигуры опредляются по формулам:

x_C = (   s_k x_k ) / S; y_C = (   s_k y_k ) / S,

где x_k, y_k - координаты центров тяжести частей фигуры; s_k - их площади; S =   s_k - площадь всей фигуры.

• Метод дополнения, являющийся частным случаем метода разбиения.  Этот метод применяется к фигурам, имеющим вырезы, если ценры тяжести фигуры без вырезов и вырезанных частей известны.  Координаты центра тяжести такой фигуры определяются по приведенным в предыдущем пункте формулам, в которых s₁, x₁, y₁ - площадь и координаты центра тяжести фигуры без вырезов; s_k, x_k, y_k (k=2, 3, ...) - площади и координаты центов тяжести вырезанных частей, причем эти площади s_k подставляются в формулы со знаком минус.