
- •38 Проблема криптографической защиты информации; понятие шифрования
- •52 Путь в графе. Цикл в графе. Связный граф
- •Компоненты связности графа. Степень вершины. Теорема о сумме степеней вершин графа.
- •Ориентированный путь. Ориентированный цикл (контур)
- •64Понятие достижимости одной вершины из другой вершины в орграфе-нету!!!
- •Множество достижимости вершины. Матрица достижимости
- •Гамильтоновы графы: Цикл с в графе g называется Гамильтоновым циклом, если с проходит без повторов вершин через все вершины графа g. Граф g – Гамильтонов, если g имеет Гамильтонов цикл.
- •Основные элементы комбинаторики. Перестановки. Размещения. Сочетания
- •Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний
Понятие множества. Конечные и бесконечные множества, пустое множество.
Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты
конечное множество (если оно не пусто) есть такое множество, элементы которого можно "пересчитать", т. е. перенумеровать так: a1, a2, ..., an, причем все элементы будут занумерованы, все числа от 1 до n будут использованы и различные элементы получат различные номера. Бесконечное же множество такое, элементы которого так "пересчитать" нельзя.
Пусто́е мно́жество (в математике) — множество, не содержащее ни одного элемента.
2 Подмножество; количество подмножеств конечного множества
Подмно́жество в теории множеств — это понятие части множества.
Если
конечное множество состоит из ![]() элементов,
то оно имеет ровно
элементов,
то оно имеет ровно ![]() подмножеств.
подмножеств.
Теоретико-множественные диаграммы. Операции над множествами (объединение, пересечение, дополнение, теоретико-множественная разность) и их свойства.
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые.
объединение двух множеств
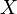 и
и 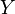 и
совокупности множеств
и
совокупности множеств 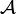 :
:
![]() или
или 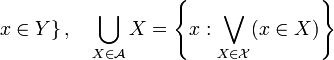
пересечение двух множеств и и совокупности множеств :
![]() и
и 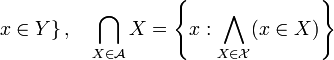
дополнение до множества
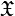 :
:
![]()
Диаграммы Венна (круги Эйлера).
Круги́ Э́йлера[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления
Важный
частный случай кругов Эйлера — диаграммы
Эйлера — Венна,
изображающие все ![]() комбинаций
комбинаций ![]() свойств,
то есть конечную булеву
алгебру.
При
свойств,
то есть конечную булеву
алгебру.
При ![]() диаграмма
Эйлера — Венна обычно изображается
в виде трёх кругов с центрами в
вершинах равностороннего треугольника и
одинаковым радиусом, приблизительно
равным длине стороны треугольника.
диаграмма
Эйлера — Венна обычно изображается
в виде трёх кругов с центрами в
вершинах равностороннего треугольника и
одинаковым радиусом, приблизительно
равным длине стороны треугольника.
8 Суждения как форма мышления
Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами В математической логике суждениям соответствуют высказывания.
Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия.
Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения.
Простые и сложные высказывания. Булевы функции.
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить,истинно оно или ложно
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
Понятие булевой функции (функции алгебры логики)
Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики)[1] от n аргументов — в дискретной математике — отображение Bn → B, где B = {0,1} — булево множество
Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу.
Понятие совершенной ДНФ. Методика представления булевой функции в виде совершенной ДНФ
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФпропозициональных букв, причём в одинаковом порядке.
Понятие совершенной КНФ. Методика представления булевой функции в виде совершенной КНФ.
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных переменных
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
15 Понятие минимальной ДНФ. Соответствие между гранями единичного N-мерного куба и элементарными произведениями
Минимальной ДНФ (МДНФ) функции f(x1, x2, …,xn) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими ДНФ, реализующими функцию f.
Методика представления булевой функции (N 3) в виде минимальной ДНФ графическим методом.
Метод Куайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных.[1][2][3] Преобразование функции можно разделить на два этапа:
на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;
на втором этапе — переход от сокращённой формы к минимальной форме
Логические схемы. Карты Карно.
Л. с. являются основой любых систем обработки дискретной информации поступает п входных сигналов и с которого снимается т выходных сигналов. При этом как независимые (логические) переменные Х 1,......, Х n, так и ф-ции Y1,..., Yn, также наз. логическими, могут принимать кол-во значения только из одного и того же конечного множества значений.
Карта Карно - это специального вида таблица, которая позволяет упростить процесс поиска минимальных форм и успешно применяется, когда число переменных не превосходит шести. Карты Карно для функций, зависящих от n переменных, представляет собой прямоугольник, разделенный на 2n клеток. Каждой клетке диаграммы ставится в соответствие двоичный n-мерный набор. Значения заданной функции f из таблицы истинности вносятся в нужные квадраты, однако если клетке соответствует 0, то обычно она остается пустой.
28 Понятие предиката
Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектомвысказывания называется то, о чём делается утверждение.
Предика́т (n-местный,
или n-арный) —
это функция с
множеством значений ![]() (или
{ложь, истина}), определённая на множестве
(или
{ложь, истина}), определённая на множестве ![]() .
Таким образом, каждый набор элементов
множества M характеризуется
либо как «истинный», либо как «ложный»
.
Таким образом, каждый набор элементов
множества M характеризуется
либо как «истинный», либо как «ложный»
36 Операции над вычетами (сложение, вычитание, умножение) и их свойства
Определение операций с функциями (f + g)(x) = f(x) + g(x) Сложение (f - g)(x) = f(x) - g(x) Вычитание (f.g)(x) = f(x).g(x) Умножение
Выполнение операций в алгебре вычетов.
Сложе́ние по мо́дулю 2 (логи́ческое сложе́ние, исключа́ющее «ИЛИ», строгая дизъюнкция, XOR, поразрядное дополнение,побитовый комплемент) — булева функция, а также логическая ибитовая операция. В случае 2 переменных результат выполнения операции является истинным тогда и только тогда, когда лишь один из аргументов является истинным. Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных 1, составляющих текущий набор - нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Сложение по модулю 2 следует отличать от простого сложения, которое соответствует обыкновенному неисключающему «или» (логической дизъюнкции).
В теории множеств сложению по модулю 2 соответствует операциясимметричной разности двух множеств.
38 Проблема криптографической защиты информации; понятие шифрования
Шифрова́ние — обратимое преобразование информации в целях сокрытия от неавторизованных лиц, с предоставлением, в это же время, авторизованным пользователям доступа к ней. Главным образом, шифрование служит задачей соблюдения конфиденциальности передаваемой информации. Важной особенностью любого алгоритма шифрования является использование ключа, который утверждает выбор конкретного преобразования из совокупности возможных для данного алгоритма.[1][2]
Криптография — наука о создании безопасных методов связи, о создании стойких (устойчивых к взлому) шифров. Она занимается поиском математических методов преобразования информации. сложность управления ключами в большой сети. Означает квадратичное возрастание числа пар ключей, которые надо генерировать, передавать, хранить и уничтожать в сети. Для сети в 10 абонентов требуется 45 ключей, для 100 уже 4950, для 1000 — 499500 и т. д.
сложность обмена ключами. Для применения необходимо решить проблему надёжной передачи ключей каждому абоненту, так как нужен секретный канал для передачи каждого ключа обеим сторонам.
39 Шифры замены. Шифр Цезаря и шифр Вижинера как частные случаи шифров замены.
Шифр простой замены, простой подстановочный шифр, моно алфавитный шифр — класс методов шифрования, которые сводятся к созданию по определённому алгоритму таблицы шифрования, в которой для каждой буквы открытого текста существует единственная сопоставленная ей буква шифр-текста
шифра Цезаря - каждый символ текста заменяется на некоторый другой, причём одинаковые символы заменяются одинаково. Если данный символ - k-ый в N-символьном алфавите, то он заменяется (k + C) mod N - ым символом алфавита. Нумерация символов начинается с нуля - не очень привычно для не прогеров, но что поделать... Здесь C - ключ шифра.
в шифре Виженера мы имеем дело с последовательностью сдвигов, циклически повторяющейся.
Перестановочные шифры.
Простой перестановочный шифр с фиксированным периодом n подразумевает разбиение исходного текста на блоки по n символов и использование для каждого такого блока некоторой перестановки E. Ключом такого шифра является используемая при шифровании перестановочная матрица P или вектор t, указывающий правило перестановки.
Криптоанализ.
Криптоанализ (от др.-греч. κρυπτός — скрытый и анализ) — наука о методах расшифровки зашифрованной информации без предназначенного для такой расшифровки ключа
В большинстве случаев под криптоанализом понимается выяснение ключа; криптоанализ включает также методы выявления уязвимости криптографических алгоритмов или протоколов.
42 Криптостойкость.
Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоятькриптоанализу. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов, недостижимого объёма перехваченных открытых и зашифрованных сообщений или же такого времени раскрытия, что по его истечению защищенная информация будет уже не актуальна, и т. д.
43 Методы замены.
неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
![]()
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
Методы перестановки.
45 Аналитические методы шифрования
Для
шифрования информации могут использоваться
аналитические методы преобразования.
Наибольшее распространение получили
методы шифрования, основанные на
использовании матричной алгебры.
Зашифрование k-го блока исходной
информации, представленного в виде
вектора Bk =
||bj|| , осуществляется путем перемножения
матрицы-ключа А=||aij||
и вектора Bk.
В результате перемножения получается
блок шифртекста в виде вектора Ck =
||ci||,
где элементы вектора Сk определяются
по формуле:
![]() ,
где
аij –
элементы матрицы-ключа;
bj –
блоки исходного текста.
Расшифрование
информации осуществляется путем
последовательного перемножения векторов
Сk;
и матрицы А-1 ,
обратной матрице А.
,
где
аij –
элементы матрицы-ключа;
bj –
блоки исходного текста.
Расшифрование
информации осуществляется путем
последовательного перемножения векторов
Сk;
и матрицы А-1 ,
обратной матрице А.
47 Принцип метода математической индукции.
Математическая индукция — метод математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
49 Понятие неориентированного графа.
Неориентированным
графом (undirected
graph) ![]() называется
пара
называется
пара ![]() ,
где
,
где ![]() —
множество вершин, а
—
множество вершин, а ![]() —
множество рёбер.
—
множество рёбер.
Неориентированным
графом
называется
тройка ![]() ,
где
,
где ![]() ,
а
и
,
а
и ![]() —
некоторые множества, причем
—
некоторые множества, причем ![]()
50 Способы задания графа.
Графы принято изображать рисунками, состоящими из точек, называемыми вершинами, и линий, называемыми дугами, соединяющими две вершины графа.
Форма дуг несущественна, важен только сам факт соединения вершин. Дуги могут пересекаться, но точки пересечения не являются вершинами графа.
Если дуги имеют направление (ориентацию), отмеченное стрелкой, то такие графы называются ориентированными или орграфами. Дуги графа часто называют ребрами.
51 Матрица смежности
Матрица смежности — один из способов представления графа в виде матрицы.
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрицаA размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины.
Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.
52 Путь в графе. Цикл в графе. Связный граф
Путь в графе G = (V,E) последовательность вершин при , таких, что две любые последовательные вершины соединены хотя бы одной дугой из E. Число k вершин в пути называется его длиной. Каждая из пар двух последовательных вершин называется его звеном
Циклом называется путь, в котором совпадают его начальная и конечная вершины
Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь
Компоненты связности графа. Степень вершины. Теорема о сумме степеней вершин графа.
Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
Степень
вершины (англ. degree,
также валентность, англ. valency)
в теории
графов —
количество рёбер графа ![]() , инцидентных вершине
, инцидентных вершине ![]() .
При подсчёте степени ребро-петля учитывается
дважды.[1] Степень
вершины обозначается как
.
При подсчёте степени ребро-петля учитывается
дважды.[1] Степень
вершины обозначается как ![]() (в
западных источниках —
(в
западных источниках — ![]() ).
Максимальная и минимальная степень
вершин графа G обозначаются соответственно
Δ(G)
и δ(G).
).
Максимальная и минимальная степень
вершин графа G обозначаются соответственно
Δ(G)
и δ(G).
Сумма степеней всех вершин графа есть четное число, равное удвоенному количеству ребер
Полный граф; формула количества рёбер в полном графе.
Полный
граф — простой граф,
в котором каждая пара различных вершин
смежна. Полный граф с
вершинами
имеет ![]() рёбер
и обозначается
рёбер
и обозначается![]() .
Является регулярным
графом степени
.
Является регулярным
графом степени ![]() .
.
Алгоритм фронта волны в графе. Методика выделения компонент связности в графе.
алгоритм
нахождения числа компонент связности, а
также выделения этих компонент на
неориентированном графе. Подобным
образом решается задача и для
ориентированного графа. В основу
рассматриваемого алгоритма выделения
компонент связности положена описанная
ранее техника поиска в глубину на
графе Г(X,U,Ф). Структура алгоритма .
является модификацией в сторону упрощения
основного алгоритма поиска в глубину.
Работа алгоритма направлена на
формирование вектора Mark[x] меток вершин
x ![]() X
графа. Элементу Mark[x] присваивается общий
номер той компоненты, которой принадлежит
вершина x
X.
Сложность алгоритма как и алгоритма
составляет O(|X|+|U|).
X
графа. Элементу Mark[x] присваивается общий
номер той компоненты, которой принадлежит
вершина x
X.
Сложность алгоритма как и алгоритма
составляет O(|X|+|U|).
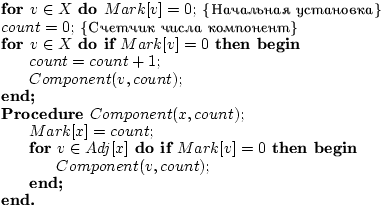
56 Мосты и разделяющие вершины (точки сочленения).
Вершину зовут разделяющей, если ее удаление увеличивает число компонент графа; ребро, обладающее этим свойством, зовут мостом. Как правило, вершины, инцидентные мосту, являются разделяющими за исключением, если одна из вершин ребра является концевой. Теорема: вершина V графа является разделяющей, если существуют такие две вершины, что любая цепь, их соединяющая, проходит через вершину V
Точка
сочленения графа — вершина ![]() графа
графа ![]() ,
при удалении которой граф
,
при удалении которой граф ![]() имеет
большекомпонент
связности,
чем исходный граф
.
имеет
большекомпонент
связности,
чем исходный граф
.
Эйлеровы графы. Теорема Эйлера (критерий эйлеровости графа).
Эйлеров граф — граф, содержащий эйлеров цикл.
Теорема Эйлера: критерий эйлеровости конечного графа Конечный неорграф эйлеров, если он связен и степени всех его вершин четны
Гамильтоновы графы. Плоские графы. Грани плоской укладки плоского графа
Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл
Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Соотношения между количествами вершин, рёбер и граней в плоском графе. Примеры неплоских графов.
Для
связного плоского графа справедливо
следующее соотношение между количеством
вершин ![]() ,
ребер
,
ребер ![]() и
граней
и
граней ![]() (включая
внешнюю грань):
(включая
внешнюю грань):
![]()
Примером неплоского графа может служить полный граф с пятью вершинами! Любые попытки начертить его плоское представление обернуться неудачей!
Деревья и их свойства. Кодирование Пруфера для деревьев с пронумерованными вершинами.
Деревом называется связный граф, не содержащий циклов. Любой (в том числе несвязный) граф без циклов называется ациклическим. Несвязный граф, каждая компонента связности которого является деревом, называется лесом.
Понятие ориентированного графа (орграфа). Способы задания орграфа. Матрица смежности для орграфа. Степень входа и степень выхода вершины. Источник. Сток.
Связи эти могут быть "направленными", как, например, в генеалогическом древе, или "ненаправленными" В соответствии с этим в теории графов выделяют два основных типа графов: ориентированные
теории
графов квадратные матрицы смежности
орграфов размера n![]() n
обозначаются буквой A как и для графов.
Элемент A(j,k) матрицы смежности орграфа
равен единице, если существует дуга из
вершины j в вершину k и равен нулю в
противном случае.
n
обозначаются буквой A как и для графов.
Элемент A(j,k) матрицы смежности орграфа
равен единице, если существует дуга из
вершины j в вершину k и равен нулю в
противном случае.
Строка матрицы смежности орграфа задаёт начало дуги, а столбец – конец дуги. Матрица смежности орграфа симметрична только в том случае, если каждая двойка смежных вершин связана симметричной парой дуг. Матрица смежности любого орграфа является булевой, то есть состоит только из нулей и единиц.
Ориентированный путь. Ориентированный цикл (контур)
ориентированный граф G = (V,E) есть пара множеств, где V — множество вершин (узлов), E — множество дуг (ориентированных рёбер). Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v → w ведет от вершины v к вершине w, при этом вершина w смежная с вершиной v.
Ориентированным графом-циклом называется ориентированная версия графа-цикла, в котором все дуги направлены в одном и том же направлении.
64Понятие достижимости одной вершины из другой вершины в орграфе-нету!!!
Множество достижимости вершины. Матрица достижимости
Матрица
достижимости простого ориентированого
графа ![]() — бинарная
матрица замыкания по
транзитивности отношения
— бинарная
матрица замыкания по
транзитивности отношения ![]() (оно
задаётся матрицей
смежности графа).
Таким образом, в матрице достижимости
хранится информация о существовании
путей между вершинами орграфа.
(оно
задаётся матрицей
смежности графа).
Таким образом, в матрице достижимости
хранится информация о существовании
путей между вершинами орграфа.
Достижимость )
— бинарное отношение ![]() на
множестве вершин графа такое,
что
на
множестве вершин графа такое,
что ![]() тогда
и только тогда, когда в графе
существует путь из
тогда
и только тогда, когда в графе
существует путь из ![]() в
в ![]()
.Достижимая вершина. От одной вершины к другой может быть несколько различных путей, кратчайший из них называется геодезической линией. Множество вершин, достижимых из данной вершины , называется множеством достижимости вершины . Орграф является односвязным, если в любой паре вершин по крайней мере одна из них является достижимой из другой.
Бесконтурные орграфы. Теорема о существовании источника и стока в бесконтурном орграфе.
Ациклический граф — граф без циклов.
67 Эйлеровы орграфы. Критерий эйлеровости орграфа. Гамильтоновы орграфы.
Эйлеров-орграф() - орграф, в котором есть эйлеров контур; для того чтобы орграф был эйлеровым необходимо и достаточно, чтобы в каждой вершине полустепень захода равнялась полустепени исхода.
Гамильтоновы графы: Цикл с в графе g называется Гамильтоновым циклом, если с проходит без повторов вершин через все вершины графа g. Граф g – Гамильтонов, если g имеет Гамильтонов цикл.
Понятие ориентированного дерева.
Ориентированным деревом называют бесконтурный ориентированный граф, у которого полустепень захода любой вершины не больше 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, полустепень захода которой равна 0.
Понятие бинарного дерева. Дисбаланс вершины в бинарном дереве
Бинарное (или двоичное) дерево — это непустое конечное множество узлов, накотором определена структура, обладающая следующими свойствами:
1. Имеется один выделенный узел г, называемый корнем данного бинарногодерева.
2. Остальные узлы (исключая корень) содержатся в двух
непересекающихсямножествах (поддеревьях) — левом и правом, каждое из которых, в своюочередь, либо пусто, либо является бинарным деревом.
На первый взгляд может показаться, что бинарное дерево — это частный слу-чай упорядоченного ориентированного дерева, в котором у каждого узла не бо-лее двух смежных. Но это не так, бинарное дерево не является упорядоченнымордеревом. Дело в том, что даже если у некоторого узла бинарного дерева име-ется только одно непустое поддерево, то всё равно известно, какое именно этоподдерево: левое или правое.
Основные элементы комбинаторики. Перестановки. Размещения. Сочетания
комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Перестановкой
множества из ![]() элементов
называется расположение элементов в
определенном порядке.
элементов
называется расположение элементов в
определенном порядке.
Размещениями
множества из
различных
элементов по ![]() элементов
элементов ![]() называются
комбинации, которые составлены из
данных
элементов
по
элементов
и отличаются либо самими элементами,
либо порядком элементов.
называются
комбинации, которые составлены из
данных
элементов
по
элементов
и отличаются либо самими элементами,
либо порядком элементов.
Сочетаниями
из
различных
элементов по ![]() элементов
называются комбинации, которые составлены
из данных
элементов
по
элементов
и отличаются хотя бы одним элементом
(иначе говоря,
-элементные
подмножества данного множества
из
элементов).
элементов
называются комбинации, которые составлены
из данных
элементов
по
элементов
и отличаются хотя бы одним элементом
(иначе говоря,
-элементные
подмножества данного множества
из
элементов).
Базовые множества для автомата: входной алфавит, выходной алфавит, множество состояний
