2.2 Практическая часть
Дано:
Нормированные вероятности отказов для элементов Qi, затраты на контроль i-ого параметра C(xi).
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Qi |
0,04 |
0,15 |
0,13 |
0,08 |
0,02 |
0,09 |
0,06 |
0,08 |
0,03 |
0,04 |
C(xi) |
5 |
1 |
4 |
2 |
6 |
3 |
2 |
3 |
1 |
1 |
Найти: Выбрать такие параметры, чтобы C≤18 при Q=Qmax.
Для удобства расчетов проранжируем таблицу следующим образом:
№ |
2 |
10 |
9 |
4 |
7 |
6 |
8 |
3 |
1 |
5 |
Qi |
0,15 |
0,04 |
0,03 |
0,08 |
0,06 |
0,09 |
0,08 |
0,13 |
0,04 |
0,02 |
C(xi) |
1 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
5 |
6 |
Решение:
Весь
имеющийся ресурс
разбиваем на отрезки единичной длины.
Таким образом,
.
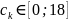При
соответствующее множество
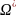состоит
из одного нулевого элемента и целевая
функция
.
При
:
в множество
можем включить один из трёх подходящих
параметров по стоимости затрат, но
выбираем тот параметр, который обладает
наибольшей вероятностью, а именно
,
вероятность которого равна
.
Вычислили значение целевой функции
и зафиксировали индекс параметра
.
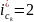При
:
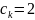на этом шаге для включения в множество
можем выбрать параметр со стоимостью,
равной единицы, тогда множество
будет состоять из двух параметров, или
же можем выбрать со стоимостью, равной
два. Соответственно выбираем
c вероятностями
.
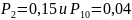Целевая функция
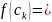
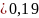и
фиксируем
.
Аналогично проводим расчёты на последующих шагах. Результат пошаговой работы алгоритма представлен в виде таблицы 2.
Таблица 2.
Выделяемое количество затратных единиц, Ck |
Значение целевой функции, f(Ck) |
Выбор на данном шаге, i*Ck
|
Выбранный массив, Ω*
|
0 |
0 |
- |
0 |
1 |
0,15 |
2 |
2 |
2 |
0,19 |
10 |
2;10 |
3 |
0,23 |
4 |
2;4 |
4 |
0,27 |
10 |
2;4;10 |
5 |
0,3 |
9 |
2;4;10;9 |
6 |
0,33 |
7 |
2;4;10;7 |
7 |
0,36 |
9 |
2;4;10;7;9 |
8 |
0,4 |
3 |
2;4;10;3 |
9 |
0,43 |
9 |
2;4;10;3;9 |
10 |
0,44 |
7 |
2;4;10;3;7 |
11 |
0,47 |
9 |
2;4;10;3;7;9 |
12 |
0,52 |
6 |
2;4;10;3;9;6 |
13 |
0,55 |
7 |
2;4;10;3;6;7 |
14 |
0,58 |
9 |
2;4;10;3;6;7;9 |
15 |
0,6 |
8 |
2;4;10;3;6;9;8 |
16 |
0,63 |
7 |
2;4;10;3;6;8;7 |
17 |
0,66 |
9 |
2;4;10;3;6;8;7;9 |
18 |
0,66 |
- |
2;4;10;3;6;8;7;9 |
Таким образом, решением является набор проверок Ω* = {X2;X3;X4;X6;X7;X8;X9;X10}.