1.3 Программные расчеты и сравнение результатов

Наряду с ручным расчётом, решение задачи реализовано с помощью программного алгоритма, написанного на языке программирования Delphi 7.0.

Листинг программы представлен в приложении 1.

Результаты программного расчёта сохраняются в текстовый файл kr1.txt и представлены на рисунке 1 для первых 4-ёх шагов, а итоговое решение на рисунке 2.

Р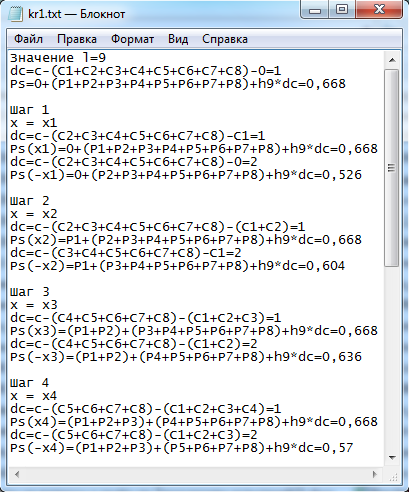 ис. 1. Результат работы программы для 4-х шагов

Р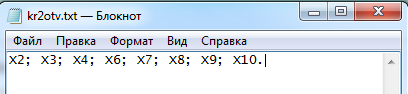 ис.2. Результат работы программы

Результаты программы и результаты ручного расчета совпали.

2. Метод динамического программирования.

2.1 Теоретическая часть

Математически задачу выбора набора параметров из заданной их совокупности можно сформулировать следующим образом.

Пусть работоспособность объекта контроля характеризуется совокупностью n взаимосвязанных параметров. Образующих множество S={x₁, x₂,…,x_n}. Проверка всех параметров из S влечет контроль всех N элементов системы и дает однозначный ответ: объект исправен, если все N элементов исправны, или неисправен. Если по крайней мере один из элементов отказал. Для x_i определено подмножество R(x_i) элементов, проверяемых при контроле i-ого параметра. Причем предполагается, что эти подмножества могут пересекаться, т.е. i, j: R(x_i) ∩ R(x_j).

Пусть Ω – некоторый набор параметров из множества S, т.е. . Тогда и , где Ω-набор контролируемых параметров, а - неконтролируемый набор. Значение из S можно представить булевым вектором, причем:

Задача выбора параметров в этом случае формулируется двояко:

1. Найти набор, для которого

Р (Ω)=max (1.11)

при

2. Найти набор Ω. Для которого:

(1.12)

при

где - апостериорная вероятность работоспособного состояния объекта контроля при положительном исходе контроля выбранных параметров;

c{x_i} - затраты на контроль i-ого параметра;

- требуемая достоверность контроля;

С – ограничение на общую стоимость контроля.

З начение зависит от принятых допущений и может быть найдено по формуле

Байеса. Так, если полагать в изделии наличие лишь одного отказа, то

(1.13)

г де - априорная вероятность безотказной работы объекта:

- нормированная вероятность отказа системы из-за отказа i-ого элемента:

(1.14)

- априорная вероятность отказа i-ого элемента.

Тогда вероятность того, что отказ будет обнаружен при проверки i-ого параметра можно вычислить по формуле:

П ри возможности наличия в ОК произвольного числа отказов

(1.15)

Д ля решения задач (1.11) и (1.12) можно использовать простой перебор вариантов, однако возникающие при этом вычислительные трудности не позволяют сделать этого даже для простых систем ( при n>10). В связи с этим комплектование набора трактуется как многошаговый процесс, состоящий из последовательного выбора отдельных параметров. В соответствии с общим принципом оптимальности, разобьем весь имеющийся ресурс стоимости С на С отрезков единичной длины. (В практических случаях заданные положительные величины c(x_i) и С можно считать всегда целыми. Если это не так, то необходимо перейти к более мелким стоимостным единицам в зависимости от разрядности дробной части.) Рассмотрим наряду с интересующей нас исходной задачей множество аналогичных задач

, аналог выражения (1.1),

г де через X_С обозначено множество неотрицательных целочисленных векторов Ω, отвечающих наборам, в которых общая стоимость проверки параметров не превосходит величины С.

Пусть

тогда при всех соответствующие множества X_Y состоят. Очевидно, из одного нулевого элемента и f(С)=0 для всех таких С. Для ресурса согласно общей схеме динамического программирования справедливы следующие рекуррентные соотношения:

( 1.16)

г де

R( )-множество тех i, для которых , начиная с номера уравнение (1.16) решается для всех i=1,n:

- сумма вероятностей элементов i-го параметра, которые пересекаются с элементами подмножества , образованного на шаге

Е сли

, то

И

(1.17)

Что приводит к условию задачи с пересекающимися параметрами.

Для решения рассматриваемой задачи рассмотрим простой численный метод, не требующий предварительного определения всех допустимых наборов и основанный на рекуррентных соотношениях (1.15). Для всех целых по формуле (1.16) вычисляют величины и при этом фиксируются индексы , на которых достигаются максимумы в (1.16). Искомый вектор формируется последовательно включение в набор параметра и подмножества , зафиксированного на шаге При этом, если , то на данном шаге этот параметр исключается из рассмотрения, так как каждый параметр может включаться в набор не более одного раза. Если на н6екотором v -м шаге окажется, что то вы качестве принимается я подмножество и фиксируется параметр , причем за принимается значение . Заметим, что если в (1.11) принять более жесткое ограничение, а именно

то последнее недопустимо, так как в этом случае может быть меньше из-за того, что он достигает на и другом подмножестве параметров.