2 8. Правила построения эпюр для изгибающего момента и поперечной силы.

Рассмотрим пример построения эпюр поперечных сил Q и изгибающих моментов М_x.

1. Изображаем расчетную схему

2. Определяем реакции опор. Первоначально выбираем произвольное направление реакций.

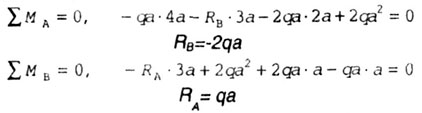
Т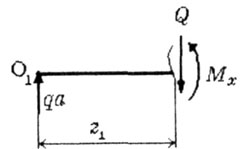 ак как реакция R_B с минусом, изменяем выбранное направление на противоположное.

Проверка:

3. Расчетная схема имеет три силовых участка.

4. 1 участок О₁,О₂:

Начало координат выбираем в крайней левой точке О₁. Рассмотрим равновесие отсеченной части бруса

В сечении возникают внутренние усилия:

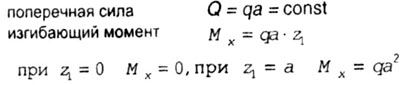
II участок O₂B;

Начало координат перенесено в начало участка O₂. На этом участке

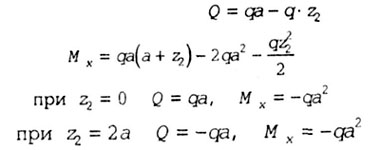
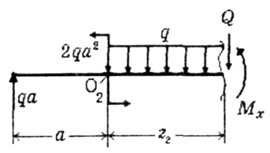
На 2-ом участке в уравнении моментов аргумент (Z₂) имеет 2-ую степень, значит эпюра будет криво второго порядка, т.е. параболой.

На 2-ом участке поперечная сила меняет знак ( начале участка +ga, а в конце -ga), значит на эпюр M_xбудет экстремум в точке, где Q = 0. Определи ем координату сечения, в котором экстремально значение М_x, приравнивая нулю выражение попе речной силы на этом участке.

Определяем величину экстремального момента:

I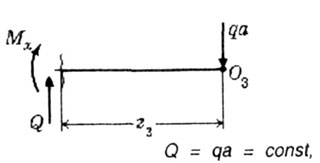 II участок ВО₃.

Начало координат на третьем участке помещено в крайней правой точке О₃ 

З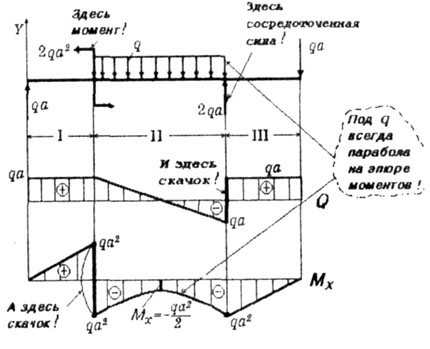 десь

5. Строим эпюры Q и М_x 

6. Проверяем правильность построения эпюр.

2 9. Дифференциальные зависимости между изгибающим моментом, поперечной силы и распределенной нагрузки.

1. Если на участке балки:

1. Поперечная сила «+», то изгибающий момент возрастает.

2. Q «-», то M убывает.

3. Q=0 (отсутствует), то М имеет постоянное значение (чистый изгиб).

4. Q проходит через меняет знак с + на -, тоM=max, в противном случае M=min.

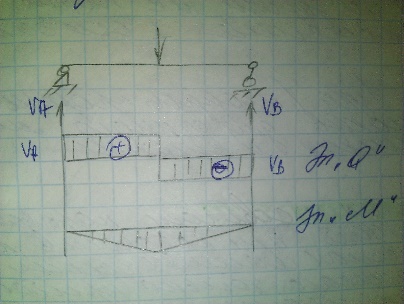2. Если на участке балки имеется сосредоточенная сила, а распределенная нагрузка отсутствует, то поперечная сила = const, M – меняется по линейному закону.

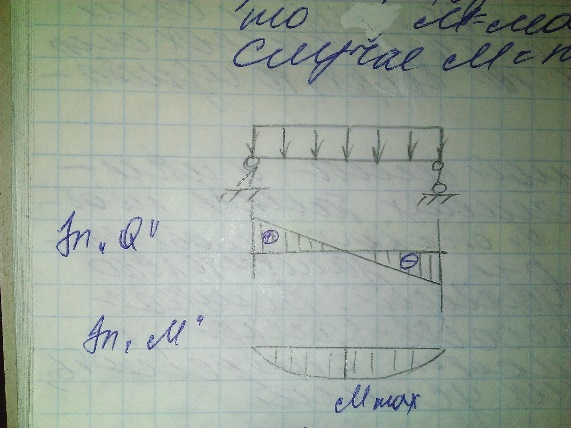
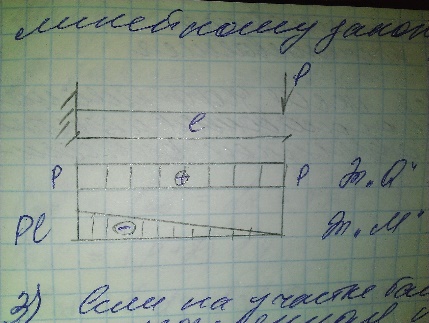3. Если на участке балки имеется равномерно распределенная нагрузка, то Q изменяется по линейному закону, а M по закону кв. параболы, обращенной выпуклостью в сторону действия нагрузки.

4. В сечении под сосредоточенной силой эпюру Q имеет скачок на величину этой силы, а Эп «М» имеет изгиб в сторону действия силы.

30. Особенности построения эпюр q и m.

Эп «Q»:

1. Если нет распределенной нагрузки, то прямая горизонтальная линия.

2. Если распределенная нагрузка , то прямая наклонная линия.

3. На Эп «Q» под точкой приложения сосредоточенной силы будет скачок на величину этой силы.

Эп «M»:

1. Если нет распределенной нагрузки, то прямая наклонная линия.

2. Если распределенная нагрузка , то парабола.

3. На Эп «M» под точкой приложения сосредоточенного момента будет скачок на величину данного момента.

31. Формула нормальных напряжений при чистом изгибе.

, где – нормальное напряжение, z – расстояние от нейтральной оси до рассматриваемого.

3 2. Эпюра нормальных напряжений по высоте сечения

изменяется пропорционально расстоянию от н.о.

1. Составим 6 уравнений равновесия:

• ;

;

– статический момент сечения

Н.о. при изгибе проходит через центр тяжести поперечного сечения.

• 

• выражения обращаются в тождество

• обращается в тождество

• ;

- центростремительный момент инерции

=> z и y – главные оси инерции (поперечного сечения)

Ось y является главной центральной осью.

• ; ; ;

- осевой момент инерции относительно оси y.

=> => => – нормальное напряжение при плоском поперечном изгибе. z - р-е от н.о. до точки в которой определяется нормальное напряжение.