15. Моменты инерции сечения: осевые, центробежный, полярный.

Sy(∑iAi)= ∑i Sy (Ai)	С. М. суммы площадей равен сумме с.м. каждой площади
	Сумма осевых моментов относительно любой пары осей проведенной через одну точку величина постоянная равная постоянному моменту

16. Главные оси и главные моменты инерции сечения. Вывод формулы для определения положения главных осей инерции.

Предположим, что задана система осей координат и известны моменты инерции lz, 1у и lzy фигуры относительно этих осей. Повернем оси координат на некоторый угол а против часовой стрелки и определим моменты инерции той же фигуры относительно новых осей координат и и v.

Из рис. 6.8 следует, что координаты какой-либо точки в обеих системах координат связаны между собой соотношениями

Момент инерции

.

Следовательно,

.	(6.29)
.	(6.30)

Центробежный момент инерции

.

(6.31)

Из полученных уравнений видно, что

,

т. е. сумма осевых моментов инерции при повороте осей координат остается величиной постоянной. Поэтому, если относительно какой-либо оси момент инерции достигает максимума, то относительно перпендикулярной ей оси он имеет минимальное значение.

Из формул (6.29) - (6.31) видно, что при повороте осей координат центробежный момент инерции меняет знак, а следовательно, существует такое положение осей, при котором центробежный момент равен нулю.

Оси. относительно которых центробежный момент инерции сечения обращается в нуль, называются главными осями а главные оси. проходящие через центр тяжести сечения - главными центральными осями инерции сечения

Моменты инерции относительно главных осей инерции сечения называются главными моментами инерции сечения и обозначаются через l1 и l2 причем l1>l2- Обычно, говоря о главных моментах, подразумевают осевые моменты инерции относительно главных центральных осей инерции.

Предположим, что оси u и v главные. Тогда

.

Отсюда

.

(6.32)

Уравнение (6.32) определяет положение главных осей инерции сечения в данной точке относительно исходных осей координат. При повороте осей координат изменяются также и осевые момента инерции. Найдем положение осей, относительно которых осевые моменты инерции достигают экстремальных значений. Для этого возьмем первую производную от Iu по α и приравняем ее нулю:

,

отсюда

.

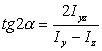К тому же результату приводит и условие dIv /dα. Сравнивая последнее выражение с формулой (6.32), приходим к заключению, что главные оси инерции являются осями, относительно которых осевые моменты инерции сечения достигают экстремальных значений.

Для упрощения вычисления главных моментов инерции формулы (6.29) - (6.31) преобразовывают, исключая из них с помощью соотношения (6.32) тригонометрические функции:

.

(6.33)

Знак плюс перед радикалом соответствует большему I1, а знак минус - меньшему I2 из моментов инерции сечения.

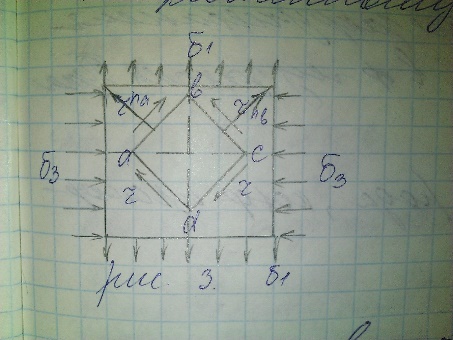
Укажем на одно важное свойство сечений, у которых осевые моменты инерции относительно главных осей одинаковы. Предположим, что оси y и z главные (Iyz=0), а Iy=Iz. Тогда согласно равенствам (6.29) - (6.31) при любом угле поворота осей α центробежный момент инерции Iuv=0, а осевые Iu=Iv.

Итак, если моменты инерции сечения относительно главных осей одинаковы, то все оси, проходящие через ту же точку сечения, являются главными и осевые моменты инерции относительно всех этих осей одинаковы: Iu=Iv=Iy=Iz. Этим свойством обладают, например, квадратные, круглые, кольцевые сечения.

Формула (6.33) аналогична формулам (3.25) для главных напряжений. Следовательно, и главные моменты инерции можно определять графическим способом методом Мора.

17. Моменты инерции простых сечений: прямоугольник, круг, треугольник.

18. Виды напряженного состояния в точке тела: линейное, плоское, пространственное.

• Линейное (осевое растяжение – сжатие)

;

• Плоское (двухосное)

; ;

;

; ;

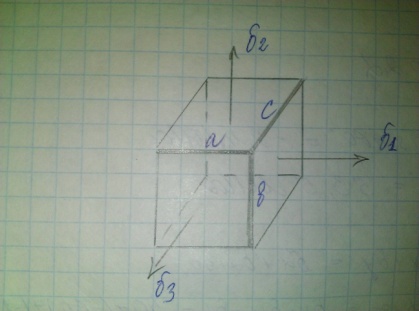• Пространственное (объемное)

; ; ;

19. Плоское напряженное состояние. Закон парности касательных напряжений.

; ;

; ;

; ;

20. Главные напряжения и главные площадки.

2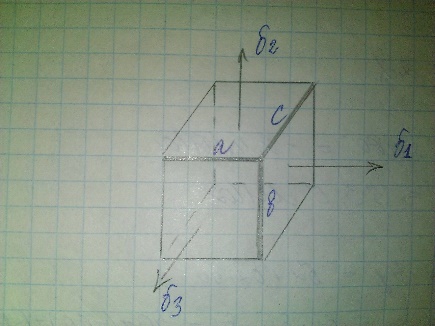 1. Пространственное напряженное состояние. Обобщенный закон Гука. Объемная деформация.

=> обобщенный закон Гука

=> для объемного

=> напряженного состояния

– продольная деформация

- поперечная деформации

- поперечная деформация

Обобщенный закон Гука устанавливает зависимость между относительной деформацией и напряжением.

- относительная объемная деформация

- объемный закон Гука

2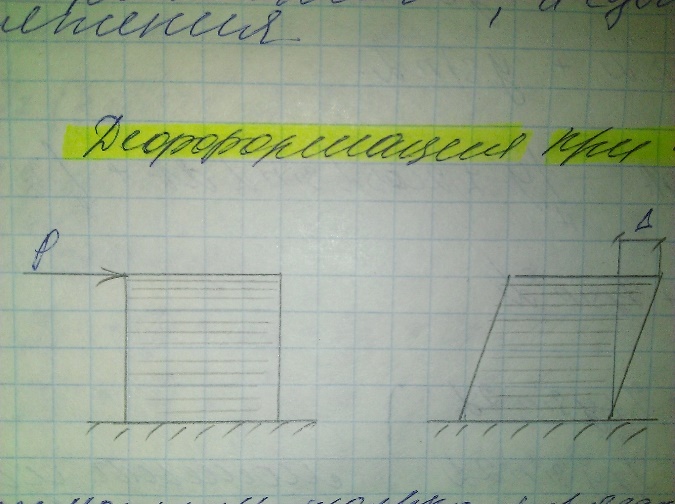 2.Чистый сдвиг. Напряжения при чистом сдвиге.

- угол сдвига

23. Деформация при сдвиге. Закон Гука при сдвиге.

По закону Гука определяются только упругие деформации.

;

Условие прочности при осевом растяжении - сжатии

24. Кручение. Крутящий момент, построение эпюр круглого сечения.

Кручение – вид деформации стрежня, при котором в его поперечном сечении действует только крутящий момент. ( ).

- угол сдвига под действием τ

;

; G – коэф. пропорциональности

25. Касательное напряжение при кручении бруса круглого сечения.

При

[ ], [ ]

26. Условия прочности при кручении. Основные типы задач на кручение.

Пример РПР №2 задача 2(5)

27. Внутренние усилия при поперечном изгибе. Правила знаков дл изгибающего момента и поперечной силы.

Изгиб – такой вид деформации, при котором в поперечном сечении стержня (балки) возникает изгибающий момент, а в общем случае и поперечная сила.

При прямом (поперечном) изгибе в сечениях балки возникает 2 внутренних силовых фактора:

1. Поперечная сила, Q

2. Изгибающий момент, M

З ависимости между этими внутренними силовыми факторами и напряжениями в поперечном сечении бруса таковы:

Q – равнодействующая внутренних касательных сил, возникающих в поперечном сечении бруса.

M – результирующий момент внутренних нормальных сил, возникающих в поперечном сечении бруса, взятый относительно н.о. этого сечения.
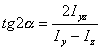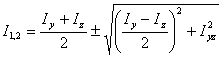