Диаграммы нагружения. Допускаемые напряжения.
Диаграмма
растяжения образца позволяет оценить
поведение материала образца в упругой
и упруго-пластической стадиях
деформирования, определить механические
характеристики материала.
Для
получения численно сопоставимых между
собой механических характеристик
материалов диаграммы растяжения образцов
перестраивают в диаграммы растяжения
материалов, т.е. в зависимость между
напряжением 
и деформацией 
,
которые определяют по формулам
,
где
-
сила, действующая на образец, 
-
начальная площадь поперечного сечения
и начальная длина расчетной части
образца.
Диаграмма растяжения материала, полученная при этих условиях (без учета изменения размеров расчетной части образца), называется условной диаграммой растяжения материала в отличие от действительной диаграммы растяжения, которую получают с учетом изменений размеров образца. Диаграмма растяжения материала зависит от его структуры, условий испытаний (температуры, скорости деформирования).
В качестве предельного напряжения в расчетах на прочность принимается:
предел текучести для пластичного материала (считается, что разрушение пластичного материала начинается при появлении в нем заметных пластических деформаций)
изображение Условие прочности жесткости допускаемое напряжение сопромат,
предел прочности для хрупкого материала, значение которого при растяжении и сжатии различно:
изображение Условие прочности жесткости допускаемое напряжение сопромат.
Для обеспечения прочности реальной детали необходимо так выбрать ее размеры и материал, чтобы возникающее в некоторой ее точке при эксплуатации наибольшее нормальное напряжение было меньше предельного:
изображение Условие прочности жесткости допускаемое напряжение сопромат
Однако даже если наибольшее расчетное напряжение в детали будет близко к предельному напряжению, гарантировать ее прочность еще нельзя.
внешние нагрузки действующие на деталь, не могут быть установлены достаточно точно,
расчетные напряжения в детали могут быть вычислены иногда лишь приближенно,
возможны отклонения действительных механических характеристик материала от расчетных характеристик.
Деталь должна быть спроектирована с некоторым расчетным коэффициентом запаса прочности
13. Условие прочности при растяжении-сжатии. Основные типы задач.
Условие прочности при растяжении (сжатии) выражается неравенством:
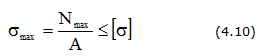
где [σ] – допускаемые напряжения, определяются как:
n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
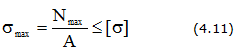
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
14. Статические моменты площади и их свойства. Определение положения центра тяжести сечения.
Статический момент площади – сумма произведений площадей элементарных площадок на их расстояние до оси.
Свойства:
Sy(∑iAi)= ∑i Sy (Ai) |
С. М. суммы площадей равен сумме с.м. каждой площади |
SZo=0 S0 |
С. М. относительно любой оси проходящей через центр тяжести равен нулю. Zo – центральная ось |
Sz = yc*A Sy = zc*A |
Если известно положение центра тяжести, то статические моменты определятся по формулам слева. Где yc, zc – координаты центра тяжести сечения |
Определение центра тяжести: пример – РПР-1 Задача 4