- •Объекты изучения. Расчетная схема.
- •Классификация внешних сил.
- •Сновные предпосылки и гипотезы в сопротивлении материалов.
- •Внутренние силы. Метод сечений.
- •Внутренние силовые факторы в поперечном сечении бруса и соответствующие им виды деформации.
- •Напряжения: нормальное, касательное, полное.
- •Деформации и перемещения.
- •Внутренние силы в стержне при центральном растяжении или сжатии.
- •Нормальные напряжения в поперечных сечениях. (можно дополнить)
- •Деформации при растяжении-сжатии. Закон Гука.
- •Механические характеристики материалов при растяжении и сжатии.
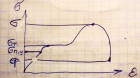
- •Диаграммы нагружения. Допускаемые напряжения.
- •13. Условие прочности при растяжении-сжатии. Основные типы задач.
- •15. Моменты инерции сечения: осевые, центробежный, полярный.
- •16. Главные оси и главные моменты инерции сечения. Вывод формулы для определения положения главных осей инерции.
- •2 8. Правила построения эпюр для изгибающего момента и поперечной силы.
- •2 9. Дифференциальные зависимости между изгибающим моментом, поперечной силы и распределенной нагрузки.
- •30. Особенности построения эпюр q и m.
- •31. Формула нормальных напряжений при чистом изгибе.
- •3 2. Эпюра нормальных напряжений по высоте сечения
- •33. Условие прочности при изгибе. Основные типы задач при изгибе.
- •34. Формула касательных напряжений при поперечном изгибе.
- •35. Эпюра касательных напряжений по высоте сечения балки (прямоугольное и двутавровое)
Напряжения: нормальное, касательное, полное.

Напряжение – внутренне усилие приходящееся на единицу площади.
Нормальное (σ) |
Внутреннее усилие приходящееся на единицу площади и направленное вдоль оси стержня. |
Касательное (τ) |
Внутреннее усилие приходящееся на единицу площади и перпендикулярное оси стержня. |
Деформации и перемещения.
Деформация – изменение формы и размеров тела.
Деформации осевого растяжения сжатия вызываются силами направленными вдоль оси стержня. При деформации возникает продольная сила.
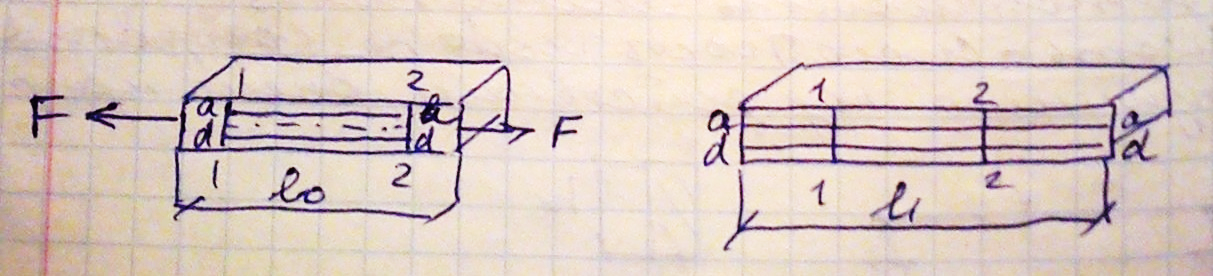
Под действием нагрузки конструкция деформируется, т.е. её форма и размеры изменяются. Это существенно влияет на законы распределения внутренних усилий в напряженном теле, хотя само по себе изменение формы, как правило, незначительно и обнаруживается в большинстве случаев только при помощи чувствительных приборов.
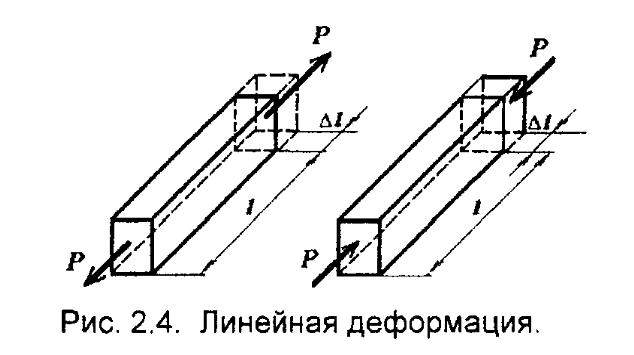
При нагружении растягивающими силами стержень удлиняется.Изменение А£ первоначальной длины £ стержня называется аб-солютным удлинением. Отношение абсолютного удлинения к первоначальной длине называется относительным удлинением
ε = ∆l/l
Внутренние силы в стержне при центральном растяжении или сжатии.

Изменение длины - ∆l
Изменение размеров поперечного сечения - ∆c и ∆b
Отношение относительной поперечной деформации к относительной продольной деформации для каждого материала величина постоянная.
Нормальные напряжения в поперечных сечениях. (можно дополнить)
Напряжение – внутренне усилие приходящееся на единицу площади.
Нормальное (σ) |
Внутреннее усилие приходящееся на единицу площади и направленное вдоль оси стержня. |
Деформации при растяжении-сжатии. Закон Гука.
Закон Гука связывает деформации с геометрическими характеристиками и усилиями. Закон выведен экспериментально.

Удлинение стержня прямо пропорционально продольной силе и длине, и обратно пропорционально жесткости стержня (ЕА)
Полная деформация = Упругая + Остаточная
∆l = ∆l упр + ∆l ост
∆l упр – исчезает после снятия внешней нагрузки
∆l ост - остается после снятия нагрузки
Закон Гука определяет только упругие деформации.

Механические характеристики материалов при растяжении и сжатии.
М. х. прочности |
|
Предел пропорциональности (σпц) |
Наибольшее нормальное напряжение при котором выполняется закон Гука.
|
Предел текучести (σт) |
Нормальное напряжение при котором происходит удлинение образца без увеличения нагрузки
|
Предел прочности (σв) |
Нормальное напряжение соответствующее наибольшей нагрузке, предшествующей разрушению
|
(σР) |
Нормальное напряжение в момент разрушения образца |
М. х. упругости |
|
Ест = 2*105 МПа |
Модуль продольной упругости |
μ = ε1/ ε |
Коэффициент Пуассона (относ. деформ. / попереч. деморм.) |
М. х. пластичности |
|
δ=(∆l ост/∆l0)*100% δ=((∆l 1-∆l0)/∆l0)*100% |
Относительное остаточное удлинение δ > 5% - пластичный; δ < 5 – хрупкий. |
ψ = (∆А/А0)*100% ψ = ((А0- Аш)/А0)*100% |
Остаточное поперечное сужение Аш – площадь шейки образца |
М. х. характеризующие энергетические свойства материала |
|
W=Fb∆lполнη |
Работа затраченная на разрыв образца η (экта) – коэффициент заполнения диаграммы (0,86 – 0,87)
|