
- •1) Число различных вариантов выбора пяти человек, когда все три первокурсника попадут в совет:
- •2) Число различных вариантов выбора пяти человек, когда в совет будут выбраны 1 первокурсник, 2 второкурсника и 2 студента 3-го курса:
- •1) Вероятность того, что в данный момент включены две камеры:
- •2) Вероятность того, что в данный момент включена только одна камера:
- •3) Вероятность того, что в данный момент включены все три камеры:
- •1) По формуле полной вероятности находим вероятность того, что наугад взятая с конвейера деталь окажется высшего качества:
- •2) Пусть взятая с конвейера деталь оказалась высшего качества.
- •Вариант 21
- •Задача № 9
- •Задача № 43
- •Задача № 21
- •Задача № 4
- •1) Вероятность того, что в мишени будет ровно одна пробоина:
- •2) Вероятность того, что не будет ни одного попадания:
- •Задача № 25
- •Задача № 32
- •Решение.
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача № 1
- •1) Число различных вариантов выбора пяти человек, когда все три первокурсника попадут в совет:
- •2) Число различных вариантов выбора пяти человек, когда в совет будут выбраны 1 первокурсник, 2 второкурсника и 2 студента 3-го курса:
- •1) По формуле полной вероятности находим вероятность того, что наугад взятая с конвейера деталь окажется высшего качества:
- •2) Пусть взятая с конвейера деталь оказалась высшего качества.
- •Задача № 39
- •Задача № 41
- •Вариант 09
- •Решение.
- •Задача 6
- •Задача 11
- •Задача 21
- •Задача 36
- •Задача 44
B
A

По расположению точек на корреляционном поле видно, что связь между X и Y является линейной, так как экспериментальные точки группируются около прямой линии. Поэтому уравнение регрессии Y на X следует искать в виде: Y = aX + b.
Для определения числовых характеристик двумерной случайной величины составим расчётную таблицу.
X |
nx |
Xnx |
X2nx |
Y |
ny |
Yny |
Y2ny |
5 |
2 |
10 |
50 |
30 |
6 |
180 |
5400 |
10 |
9 |
90 |
900 |
40 |
9 |
360 |
14400 |
15 |
49 |
735 |
11025 |
50 |
50 |
2500 |
125000 |
20 |
16 |
320 |
6400 |
60 |
21 |
1260 |
75600 |
25 |
21 |
525 |
13125 |
70 |
14 |
980 |
68600 |
30 |
3 |
90 |
2700 |
∑ |
100 |
5280 |
289000 |
∑ |
100 |
1770 |
34200 |
|
|
|
|
Числовые характеристики выборки:




Выборочный коэффициент линейной корреляции:

Уравнение прямой линии регрессии Y на Х:

Уравнение прямой линии регрессии X на Y:

Строим линии (1) и (2) и экспериментальные точки.

Задача № 7
В ящике 6 белых, 7 красных и 3 черных шара. Какова вероятность того, что вынутые 2 шара окажутся разного цвета?
Решение
Общее
число различных вариантов извлечения
2-х шаров из данных (6+7+3)=16-ти шаров:

Два
извлечённых шара будут разного цвета,
если один шар будет белый, другой –
красный; один – белый, другой – чёрный;
один – красный, другой – чёрный.
Соответствующее число различных
вариантов извлечения шаров:

Искомая
вероятность:

Ответ: 0,675.
Задача № 14
Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе — 0,9, в третье — 0,8. Найти вероятность того, что два отделения получат газеты вовремя, а одно — с опозданием.
Решение
Пусть pi – вероятность своевременной доставки газеты в i-ое отделение. Тогда вероятность того, что в i-ой отделение газета не будет доставлена вовремя: qi = 1 – pi.
Тогда вероятность того, что два отделения получат газеты вовремя, а одно — с опозданием:

Ответ: 0,283.
Задача № 21
На предприятии 30% приборов монтируется с применением микромодулей, остальные — с применением интегральных схем. Надежность прибора с применением микромодулей — 0,9, интегральных схем — 0,85. Найти:
вероятность надежной работы наугад взятого прибора;
вероятность того, что прибор был монтирован с интегральной схемой, если он исправен.
Решение
Пусть Н1 = {Прибор монтировался с применением микромодулей},
H2 = {Прибор монтировался с применением интегральных схем},
A = {Прибор работал надёжно}.
По условию имеем вероятности:

а) Вероятность надёжной работы наугад взятого прибора (по формуле полной вероятности):

б) Вероятность того, что прибор был монтирован с интегральной схемой, если он исправен (по формуле Байеса):

Ответ: а) 0,865; б) 0,688.
Задача № 38
В партии 10% нестандартных деталей, т.е. вероятность появления нестандартных деталей одинакова и равна 0,1. Наудачу отобраны 4 детали. Определить ряд распределения, построить многоугольник распределения, функцию распределения случайной величины Х — числа нестандартных деталей среди четырех отобранных. Найти математическое ожидание и дисперсию.
Решение
Возможные значения СВ Х: 0; 1; 2; 3; 4. Вероятность появления нестандартной детали в каждом испытании равна р=0,1. Находим вероятности соответствующих значений СВ Х по формуле Бернулли:

Строим ряд распределения СВ Х.
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
Проверка:

Строим многоугольник распределения.

Для построения функции распределения F(x) составим вспомогательную таблицу.
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
∑pi |
0,6561 |
0,9477 |
0,9963 |
0,9999 |
1 |
Функция
распределения СВ Х:

Строим график функции F(x).
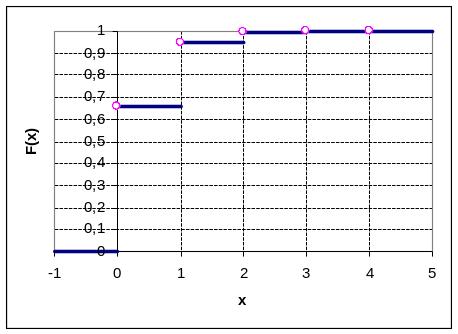
Для определения числовых характеристик СВ Х составим расчётную таблицу.
xi |
pi |
xipi |
|
0 |
0,6561 |
0 |
0 |
1 |
0,2916 |
0,2916 |
0,2916 |
2 |
0,0486 |
0,0972 |
0,1944 |
3 |
0,0036 |
0,0108 |
0,0324 |
4 |
0,0001 |
0,0004 |
0,0016 |
∑ |
1 |
0,4 |
0,52 |
Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Математическое ожидание и дисперсию можно найти иначе:

Задача № 41
Приводятся результаты наблюдений (xi, yi) над двумерной величиной (Х, Y). Используя эти экспериментальные данные, необходимо:
1) построить корреляционное поле. По характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости Y от X и X от Y;
2) определить числовые характеристики ;
3) написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
4) вычислить коэффициент корреляции.
x y |
10 |
20 |
30 |
40 |
ny |
20 |
1 |
|
|
|
1 |
40 |
4 |
1 |
|
|
5 |
60 |
1 |
15 |
1 |
|
17 |
80 |
|
2 |
13 |
|
15 |
100 |
|
|
2 |
1 |
3 |
120 |
|
|
|
9 |
9 |
nx |
6 |
18 |
16 |
10 |
n = 50 |
Решение
По данной таблице находим координаты экспериментальных точек:

Строим корреляционное поле по найденным точкам.
D
C
B
A
По расположению точек на корреляционном поле видно, что связь между X и Y является линейной. Поэтому уравнение регрессии Y на X следует искать в виде: Y = aX + b.
Для определения числовых характеристик двумерной случайной величины составим расчётную таблицу.
X |
nx |
Xnx |
X2nx |
Y |
ny |
Yny |
Y2ny |
10 |
6 |
60 |
600 |
20 |
1 |
20 |
400 |
20 |
18 |
360 |
7200 |
40 |
5 |
200 |
8000 |
30 |
16 |
480 |
14400 |
60 |
17 |
1020 |
61200 |
40 |
10 |
400 |
16000 |
80 |
15 |
1200 |
96000 |
∑ |
50 |
1300 |
38200 |
100 |
3 |
300 |
30000 |
|
|
|
|
120 |
9 |
1080 |
129600 |
|
|
|
|
∑ |
50 |
3820 |
325200 |
Числовые характеристики выборки:




Выборочный коэффициент линейной корреляции:

Уравнение прямой линии регрессии Y на Х:

Уравнение прямой линии регрессии X на Y:

Строим линии (1) и (2) и экспериментальные точки.
(1)
C
B
Задача № 4
В урне 14 красных и 8 черных шаров. Найти вероятность того, что из пяти взятых наугад шаров красных будет не более двух.
Решение
Всего
в урне (14+8)=22 шара. Число различных
вариантов извлечения из урны 5-ти шаров:

Число различных вариантов извлечения 5-ти шаров, когда среди них будет красных шаров:
-
ноль:

-
один:

-
два:

Следовательно, число различных вариантов извлечения 5-ти шаров, когда среди них красных шаров будет не более двух:

Искомая
вероятность:

Ответ: 0,2329.
Задача № 13
Три стрелка стреляют по одной мишени. Вероятность попадания каждого из стрелков соответственно равны р1 = 0,4; р2 = 0,5; р3 = 0,7. Найти вероятность того, что в результате одновременного выстрела в мишени будет:
ровно одна пробоина;
хотя бы одна пробоина.
Решение
Вероятность
промаха i-го
стрелка:

1) Вероятность того, что в мишени будет ровно одна пробоина:

2) Вероятность того, что не будет ни одного попадания:

Тогда вероятность наличия хотя бы одной пробоины:

Ответ: 1) 0,36; 2) 0,91.
Задача № 25
В дисплейном классе имеется 10 персональных компьютеров первого типа и 25 — второго. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,95, а на компьютере второго типа — 0,8. Найти вероятность того, что:
на случайно выбранном компьютере за время работы не произойдет сбоя;
компьютер, во время работы на котором не произошло сбоя, - второго типа.
Решение
Пусть Н1 = {Компьютер принадлежит к первому типу}, H2 = {Компьютер принадлежит ко второму типу}, A = {На компьютере не произойдёт сбоя}.
По условию имеем вероятности:

а) Вероятность того, что на случайно выбранном компьютере за время работы не произойдет сбоя (по формуле полной вероятности):

б) Вероятность того, что компьютер, во время работы на котором не произошло сбоя, - второго типа (по формуле Байеса):

Ответ: а) 0,8429; б) 0,6779.
Задача № 32
Дана дискретная случайная величина Х. Построить: 1) ряд распределения; 2) многоугольник распределения; 3) функцию распределения F(x). Рассчитать: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение.
Партия из 20 изделий содержит 5 бракованных. Из партии выбирают 5 изделий. Х — число бракованных изделий, содержащихся в случайной выборке.
Решение
Возможные значения СВ Х: 0; 1; 2; 3; 4; 5.
Находим соответствующие вероятности:






Строим ряд распределения СВ Х.
xi |
0 |
1 |
2 |
3 |
4 |
5 |
pi |
0,19369 |
0,44021 |
0,29347 |
0,06772 |
0,00484 |
0,00007 |
Проверка:

Строим многоугольник распределения.

Для построения функции распределения составим вспомогательную таблицу.
xi |
0 |
1 |
2 |
3 |
4 |
5 |
pi |
0,19369 |
0,44021 |
0,29347 |
0,06772 |
0,00484 |
0,00007 |
∑pi |
0,19369 |
0,63390 |
0,92737 |
0,99509 |
0,99993 |
1 |
Функция распределения:

Строим график функции F(x).
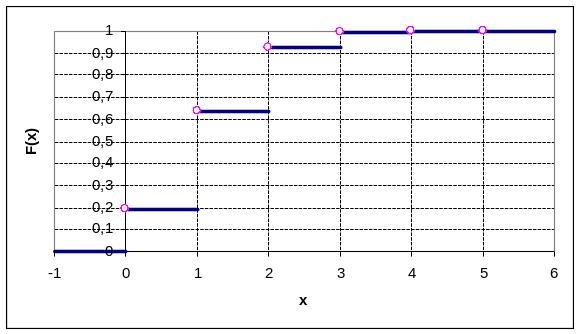
Для определения числовых характеристик СВ Х составим расчётную таблицу.
xi |
pi |
xipi |
|
0 |
0,19369 |
0 |
0 |
1 |
0,44021 |
0,44021 |
0,44021 |
2 |
0,29347 |
0,58694 |
1,17388 |
3 |
0,06772 |
0,20316 |
0,60948 |
4 |
0,00484 |
0,01936 |
0,07744 |
5 |
0,00007 |
0,00035 |
0,00175 |
∑ |
1 |
1,25002 |
2,30276 |
Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Задача № 47
Приводятся результаты наблюдений (xi, yi) над двумерной величиной (Х, Y). Используя эти экспериментальные данные, необходимо:
1) построить корреляционное поле. По характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости Y от X и X от Y;
2) определить числовые характеристики ;
3) написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
4) вычислить коэффициент корреляции.
x y |
2 |
7 |
12 |
17 |
22 |
ny |
100 |
2 |
4 |
|
|
|
6 |
110 |
|
6 |
2 |
|
|
8 |
120 |
|
|
3 |
50 |
2 |
55 |
130 |
|
|
1 |
10 |
6 |
17 |
140 |
|
|
|
7 |
7 |
14 |
nx |
2 |
10 |
6 |
67 |
15 |
n = 100 |
P.S.
В условии исправлена опечатка, так как
по исходным данным методички получаем:

Решение
По данной таблице находим координаты экспериментальных точек:

Строим корреляционное поле по найденным точкам.
E
D
С
В
А
По расположению точек на корреляционном поле видно, что связь между X и Y является линейной, так как точки группируются около прямой линии. Поэтому уравнение регрессии Y на X следует искать в виде: Y = aX + b.
Для определения числовых характеристик двумерной случайной величины составим расчётную таблицу.
X |
nx |
Xnx |
X2nx |
Y |
ny |
Yny |
Y2ny |
2 |
2 |
4 |
8 |
100 |
6 |
600 |
60000 |
7 |
10 |
70 |
490 |
110 |
8 |
880 |
96800 |
12 |
6 |
72 |
864 |
120 |
55 |
6600 |
792000 |
17 |
67 |
1139 |
19363 |
130 |
17 |
2210 |
287300 |
22 |
15 |
330 |
7260 |
140 |
14 |
1960 |
274400 |
∑ |
100 |
1615 |
27985 |
∑ |
100 |
12250 |
1510500 |
Числовые характеристики выборки:



Выборочный коэффициент линейной корреляции:

Уравнение прямой линии регрессии Y на Х:

Уравнение прямой линии регрессии X на Y:

Строим линии (1) и (2) и экспериментальные точки.
E
D
C
B
A
(1)
Задание 2. В партии из 15 радиоприемников 5 неисправных. Для проверки наугад выбрали 3 радиоприемника. Найти вероятность того, что в числе выбранных исправных приемников будет не менее двух.
Решение:
Событие А- исправных приемников не менее 2-х, т.е. 3 и более.
Р(А)
=
 ;
;
n=
 =
=
 =
=
 =
2400.
=
2400.
m=
 x
x
 =
=
 x
x
 =
=
 х
х
 =
=
 =
8,4.
=
8,4.
Р(А)=
 =
285,71
=
285,71
Задание 17. В двух ящиках находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 18, 8 и 6. Из каждого ящика наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета?
Событие А- оба шара одного цвета?
Решение:
Вероятность
того, что из первого ящика извлеченный
шар будет белым =

Вероятность
того, что из первого ящика извлеченный
шар будет черным =

Вероятность
того, что из первого ящика извлеченный
шар будет красным =

Вероятность
того, что из второго ящика извлеченный
шар будет белым =
Вероятность
того, что из второго ящика извлеченный
шар будет черным =
Вероятность
того, что из второй урны извлеченный
шар будет красным =

Р(А)=
х
 х
х
х
х
 =
=
 =
=
 =
495
=
495
Задание 26. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела — 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Какова вероятность того, что выстрел произведен из винтовки с прицелом?
Решение: Событие А- выстрел произведен из винтовки с прицелом.
Р
(оптического прицела)=
 =
0,44.
=
0,44.
Р
(без оптического прицела) =
 = 0,56.
= 0,56.
Вероятность того, что стрелок попал в мишень из винтовки без оптического прицела больше и она = 0,56. Вероятность попадения в мишень из винтовки с оптическим прицелом = 0,44.
36. Стрелок трижды стреляет в мишень. Вероятность промаха при одном выстреле равна 0,1. Построить многоугольник распределения, закон и функцию распределения случайной величины Х — числа промахов при 3 выстрелах. Найти математическое ожидание и дисперсию Х.
Решение.
Случайная величина (СВ) Х – число промахов - может принимать значения 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли при р = 0,1, q = 1- 0,1 = 0,9.
 ,
,
 ,
,
 ,
,

Ряд распределения СВ Х имеет вид:
xi |
0 |
1 |
2 |
3 |
pi |
0,729 |
0,243 |
0,027 |
0,001 |
Многоугольник распределения

Функция распределения по определению равна F(x) = P( X < x ) и запишется:

График показан на рисунке.
 F(x)
F(x)




 1
1



0,8
0,6
0,4
0,2


1 2 3 x
Вычисляем математическое ожидание и дисперсию:


D[x] = 0,36 - (0,3)2 = 0,27.
Задание 47.
x |
2 |
7 |
12 |
17 |
22 |
ny |
y |
||||||
100 |
2 |
4 |
|
|
|
6 |
110 |
|
6 |
2 |
|
|
8 |
120 |
|
|
3 |
50 |
2 |
55 |
130 |
|
|
1 |
10 |
6 |
17 |
140 |
|
|
|
4 |
7 |
14 |
nx |
2 |
10 |
6 |
64 |
15 |
n = 100 |
Решение.
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D, E, F.
Точка А
имеет координаты
,
где
 ,
,
 ,
то есть
,
то есть
 ;
;
точка
 ,
то есть B(7;
106);
,
то есть B(7;
106);
точка
 ,
то есть C(12;
118,89);
,
то есть C(12;
118,89);
точка
 ,
то есть D(17;
12,81);
,
то есть D(17;
12,81);
точка
 ,
то есть E(22;
133,33).
,
то есть E(22;
133,33).
.
Нетрудно видеть, что связь между X и Y является линейной. Поэтому уравнение регрессии ищем в виде: .
2) По известным формулам находим числовые характеристики:


Находим и :




3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определим для полной задачи :

Тогда

Уравнение прямой регрессии Y на X имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле

Тогда получаем следующее уравнение регрессии Y на X:

Составим теперь уравнение регрессии X на Y:
.


Построим
прямые регрессий
 и
и .
.


Задача 1
В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
Решение
Пусть событие А состоит в том, что 4 извлеченные детали окажутся окрашенными. Вероятность события А найдем по классическому определению вероятности
 ,
,
где m — число равновозможных элементарных событий, благоприятных для события А, т. е. для нашей задачи m — это число способов, которыми можно выбрать 4 окрашенные детали из 6 имеющихся окрашенных деталей.
Так как порядок выбора не имеет значения, то
 ;
;
n — число всех возможных элементарных событий, то есть в нашей задаче n — это число способов, которыми можно извлечь 4 детали из 10 деталей в ящике.
Так как порядок отбора не имеет значения, то
 .
.
Итак,
 .
.
Задача 2
Из партии швейных изделий отбираются изделия первого сорта. Вероятность того, что наудачу взятое изделие первого сорта, равна 0,84. Найти вероятность того, что из двух взятых изделий:
а) только одно первого сорта;
б) хотя бы одно первого сорта.
Решение
а) Пусть первое
изделие первого сорта — это событие
 ,
а второе изделие первого сорта —
,
а второе изделие первого сорта —
 .
Событие В,
состоящее в том, что выздоровеет только
одно животное, будет суммой двух
несовместных событий
.
Событие В,
состоящее в том, что выздоровеет только
одно животное, будет суммой двух
несовместных событий
 ,
т. е.
,
т. е.
 .
.
Воспользовавшись теоремой сложения и умножения вероятностей для независимых событий, получим


 .
.
б) Событие С, состоящее в том, что хотя бы одно изделие первого сорта, является суммой двух совместных событий А1 и А2, то есть либо первое изделие первого сорта, либо второе изделие первого сорта, либо оба изделия первого сорта.
По теореме сложения вероятностей двух совместных событий имеем:
 .
.
Поскольку и — независимые события, то для них верно:

Задача 3
В магазине продаются электролампы производства 3 заводов, причем доля первого завода — 30%, второго — 50, третьего — 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%.
1) Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной? 2)Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе.
Решение
Обозначим через A = {выбранная лампа оказалась бракованной}.
 {выбранная лампа
изготовлена на i-м
заводе},
{выбранная лампа
изготовлена на i-м
заводе},
 .
Тогда
.
Тогда
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
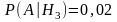 .
По формуле полной вероятности вероятность
того, что случайно выбранная лампа
оказалась бракованной, получим
.
По формуле полной вероятности вероятность
того, что случайно выбранная лампа
оказалась бракованной, получим

 .
.
Для ответа на второй вопрос задачи выпишем формулу Байеса для этого случая
 .
.
Задача 4
Заводом выпущено n компрессоров. Составить закон распределения случайной величины Х — числа компрессоров, Соответствующих техническим требованиям заказчика, построить многоугольник распределения этой случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, если вероятность того, что любой отдельно взятый компрессор соответствует техническим требованиям заказчика, равна р. k = 4; p = 0,55.
Решение
Так как вероятность
того, что любой отдельно взятый компрессор
соответствует техническим требованиям
заказчика постоянна
 и не зависит от исходов предыдущих
испытаний, то случайная величина Х
— числа компрессоров, соответствующих
техническим требованиям заказчика,
подчиняется биномиальному закону
распределения, то есть Х
= 0, 1, 2, 3, 4 и
и не зависит от исходов предыдущих
испытаний, то случайная величина Х
— числа компрессоров, соответствующих
техническим требованиям заказчика,
подчиняется биномиальному закону
распределения, то есть Х
= 0, 1, 2, 3, 4 и
 (формула Бернулли).
(формула Бернулли).
Найдем эти вероятности:

 ;
;

 ;
;

 ;
;

 ;
;

 .
.
Следовательно, ряд распределения случайной величины Х можно задать таблицей:
Х |
0 |
1 |
2 |
3 |
4 |
Р |
0,04100625 |
0,200475 |
0,3675375 |
0,299475 |
0,09150625 |
Построим многоугольник распределения дискретной случайной величины:

Вычислим математическое ожидание случайной величины Х:


 .
.
Далее найдем дисперсию


 .
.
Среднее квадратическое отклонение равно:
 .
.
Задача 5
Приводятся
результаты наблюдений
 над двумерной случайной величины
над двумерной случайной величины
 .
Используя эти экспериментальные данные,
необходимо:
.
Используя эти экспериментальные данные,
необходимо:
построить корреляционное поле, по характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости Y на X и X на Y (рекомендуется использовать модель линейной регрессии).
определить числовые характеристики выборки
 ;
;
написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
вычислить коэффициент корреляции.
Y |
X |
|||||
25 |
35 |
45 |
55 |
65 |
|
|
20 |
1 |
1 |
|
|
|
2 |
25 |
1 |
4 |
3 |
|
|
8 |
30 |
1 |
5 |
5 |
2 |
|
13 |
35 |
|
2 |
9 |
4 |
|
15 |
40 |
|
|
2 |
4 |
3 |
9 |
45 |
|
|
|
1 |
2 |
3 |
|
3 |
12 |
19 |
11 |
5 |
|
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D, E, F.
Точка А
имеет координаты
,
где
 ,
,
 ,
то есть
,
то есть
 ;
;
точка
 ,
то есть B(35;
22,33);
,
то есть B(35;
22,33);
точка
 ,
то есть C(45;
32,63);
,
то есть C(45;
32,63);
точка
 ,
то есть D(55;
36,82);
,
то есть D(55;
36,82);
точка
 ,
то есть E(65;
42).
,
то есть E(65;
42).

Нетрудно видеть, что связь между X и Y является линейной. Поэтому уравнение регрессии ищем в виде: .
2) По известным формулам находим числовые характеристики:




Находим и :






3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определим для полной задачи :


 .
.
 .
.
Тогда

Уравнение прямой регрессии Y на X имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле

Тогда получаем следующее уравнение регрессии Y на X:

Составим теперь уравнение регрессии X на Y:
.


Построим прямые
регрессий
 и
и
 .
.
|
|
Из 13 женщин и 12 мужчин составляется наугад группа из 6 человек. Какова вероятность того, что в нее попадут 3 женщины и 3 мужчины?
Решение:
Решение
Пусть событие А
состоит в том, что 6 человек выбранные
наугад в группу являются 3 женщины и 3
мужчины. Для того, того чтобы в группе
было 3 женщины их следует выбрать из 13
женщин, число способов такого выбора
равно
 .
Остальные 3 человека – мужчины, выбираются
из 12, это можно осуществить
.
Остальные 3 человека – мужчины, выбираются
из 12, это можно осуществить
 способами. По теореме умножения число
способов, благоприятствующих сбытию,
равно
способами. По теореме умножения число
способов, благоприятствующих сбытию,
равно
 .
Число всех способов равно числу способов
выбора 6 человек из 25 человек, т.е.
.
Число всех способов равно числу способов
выбора 6 человек из 25 человек, т.е.
 .
Поэтому искомая вероятность
.
Поэтому искомая вероятность
 равна:
равна:
 ,
,
Решая получаем:


Итак,

Ответ:
 .
.
В коробке 3 синих и 7 красных шариков. Наугад извлекается один шарик, затем второй. Найти вероятность того, что первый шарик — красный, а второй — синий.
Решение:
Пусть первый шарик красный — это событие , а второй шар – синий событие — . Событие В, состоящее в том, что первый шар красный, второй – синий. Она равна вероятности.

Ответ: Вероятность, что первый шар будет красный, а второй – синий равна 0,2(3).
Для поисков спускаемого аппарата космического корабля выделено 4 вертолета первого типа и 6 вертолетов второго типа. Каждый вертолет первого типа обнаруживает находящийся в районе поиска аппарат с вероятностью 0,5, второго типа — с вероятностью 0,75. 1) Найти вероятность того, что наугад выбранный вертолет обнаружит аппарат. 2) К какому типу вероятнее всего принадлежит вертолет, обнаруживший спускаемый аппарат?
Обозначим через A = {выбранный вертолет обнаружит аппарат}.
{выбранный
вертолет
i-го
тип},
 .
Тогда
.
Тогда
 ,
,
 ,
,
 ,
,
 .
По формуле полной вероятности вероятность
того, что наугад выбранный вертолет
обнаружит аппарат, получим
.
По формуле полной вероятности вероятность
того, что наугад выбранный вертолет
обнаружит аппарат, получим
 .
.
Для ответа на второй вопрос задачи выпишем формулу Байеса для каждого случая:
 ;
;
 .
.
Ответ: Вертолет, обнаруживший спускаемый аппарат принадлежит ко второму типу.
Дана дискретная случайная величина Х. Построить: 1) ряд распределения; 2) многоугольник распределения; 3) функцию распределения F(x). Рассчитать: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение.
Вероятность того, что стрелок попадает в мишень при одном выстреле, равна 0,8. Х — число попаданий при 4 выстрелах.
Решение
Так как вероятность
того, что любой отдельный взятый выстрел
попадает в мишень и вероятность равна
 и не зависит от предыдущих попаданий,
то случайная величина Х
— число попаданий, подчиняется
биномиальному закону распределения,
то есть Х =
0, 1, 2, 3, 4 и
(формула Бернулли).
и не зависит от предыдущих попаданий,
то случайная величина Х
— число попаданий, подчиняется
биномиальному закону распределения,
то есть Х =
0, 1, 2, 3, 4 и
(формула Бернулли).
Найдем эти вероятности:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Следовательно, ряд распределения случайной величины Х можно задать таблицей:
Х |
0 |
1 |
2 |
3 |
4 |
Р |
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
Построим многоугольник распределения дискретной случайной величины:
Многоугольник распределения

Вычислим математическое ожидание случайной величины Х:
 .
.
Далее найдем дисперсию

 .
.
Среднее квадратическое отклонение равно:
 .
.
Приводятся результаты наблюдений над двумерной случайной величины (X,Y). Используя эти экспериментальные данные, необходимо:
построить корреляционное поле. По характеру расположения точек на корреляционное поле подобрать математическую модель регрессионной зависимости Y от X и X от Y (рекомендуется использовать модель линейной регрессии);
определить числовые характеристики ;
написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
вычислить коэффициент корреляции.
x |
2 |
7 |
12 |
17 |
22 |
ny |
y |
||||||
100 |
2 |
4 |
|
|
|
6 |
110 |
|
6 |
2 |
|
|
8 |
120 |
|
|
3 |
50 |
2 |
55 |
130 |
|
|
1 |
10 |
6 |
17 |
140 |
|
|
|
4 |
7 |
14 |
nx |
2 |
10 |
6 |
64 |
15 |
n = 100 |
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D, E.
Точка А
имеет координаты
,
где
 ,
,
 ,
то есть
,
то есть
 ;
;
точка
 ,
то есть B(7;106);
,
то есть B(7;106);
точка
 ,
то есть C(12;
118,3);
,
то есть C(12;
118,3);
точка
 ,
то есть D(17;
130,9);
,
то есть D(17;
130,9);
точка
 ,
то есть E(22;
133,3).
,
то есть E(22;
133,3).

Нетрудно видеть, что связь между X и Y является линейной. Поэтому уравнение регрессии ищем в виде: .
2) По известным формулам находим числовые характеристики:


Находим и :




3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определим для полной задачи :

Тогда

Уравнение прямой регрессии Y на X имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле

Тогда получаем следующее уравнение регрессии Y на X:

Составим теперь уравнение регрессии X на Y:
.


Построим прямые
регрессий
 и
и
 .
.
|
|
Из 13 женщин и 12 мужчин составляется наугад группа из 6 человек. Какова вероятность того, что в нее попадут 3 женщины и 3 мужчины?
Решение:
Решение
Пусть событие А состоит в том, что 6 человек выбранные наугад в группу являются 3 женщины и 3 мужчины. Для того, того чтобы в группе было 3 женщины их следует выбрать из 13 женщин, число способов такого выбора равно . Остальные 3 человека – мужчины, выбираются из 12, это можно осуществить способами. По теореме умножения число способов, благоприятствующих сбытию, равно . Число всех способов равно числу способов выбора 6 человек из 25 человек, т.е. . Поэтому искомая вероятность равна:
,
Решая получаем:
Итак,
Ответ: .
В коробке 3 синих и 7 красных шариков. Наугад извлекается один шарик, затем второй. Найти вероятность того, что первый шарик — красный, а второй — синий.
Решение:
Пусть первый шарик красный — это событие , а второй шар – синий событие — . Событие В, состоящее в том, что первый шар красный, второй – синий. Она равна вероятности.
Ответ: Вероятность, что первый шар будет красный, а второй – синий равна 0,2(3).
Для поисков спускаемого аппарата космического корабля выделено 4 вертолета первого типа и 6 вертолетов второго типа. Каждый вертолет первого типа обнаруживает находящийся в районе поиска аппарат с вероятностью 0,5, второго типа — с вероятностью 0,75. 1) Найти вероятность того, что наугад выбранный вертолет обнаружит аппарат. 2) К какому типу вероятнее всего принадлежит вертолет, обнаруживший спускаемый аппарат?
Обозначим через A = {выбранный вертолет обнаружит аппарат}.
{выбранный вертолет i-го тип}, . Тогда , , , . По формуле полной вероятности вероятность того, что наугад выбранный вертолет обнаружит аппарат, получим
.
Для ответа на второй вопрос задачи выпишем формулу Байеса для каждого случая:
;
.
Ответ: Вертолет, обнаруживший спускаемый аппарат принадлежит ко второму типу.
Дана дискретная случайная величина Х. Построить: 1) ряд распределения; 2) многоугольник распределения; 3) функцию распределения F(x). Рассчитать: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение.
Вероятность того, что стрелок попадает в мишень при одном выстреле, равна 0,8. Х — число попаданий при 4 выстрелах.
Решение
Так как вероятность того, что любой отдельный взятый выстрел попадает в мишень и вероятность равна и не зависит от предыдущих попаданий, то случайная величина Х — число попаданий, подчиняется биномиальному закону распределения, то есть Х = 0, 1, 2, 3, 4 и (формула Бернулли).
Найдем эти вероятности:
;
;
;
;
.
Следовательно, ряд распределения случайной величины Х можно задать таблицей:
Х |
0 |
1 |
2 |
3 |
4 |
Р |
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
Построим многоугольник распределения дискретной случайной величины:
Многоугольник распределения

Вычислим математическое ожидание случайной величины Х:
.
Далее найдем дисперсию
.
Среднее квадратическое отклонение равно:
.
Приводятся результаты наблюдений над двумерной случайной величины (X,Y). Используя эти экспериментальные данные, необходимо:
построить корреляционное поле. По характеру расположения точек на корреляционное поле подобрать математическую модель регрессионной зависимости Y от X и X от Y (рекомендуется использовать модель линейной регрессии);
определить числовые характеристики ;
написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
вычислить коэффициент корреляции.
x |
2 |
7 |
12 |
17 |
22 |
ny |
y |
||||||
100 |
2 |
4 |
|
|
|
6 |
110 |
|
6 |
2 |
|
|
8 |
120 |
|
|
3 |
50 |
2 |
55 |
130 |
|
|
1 |
10 |
6 |
17 |
140 |
|
|
|
4 |
7 |
14 |
nx |
2 |
10 |
6 |
64 |
15 |
n = 100 |
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D, E.
Точка А имеет координаты , где , , то есть ;
точка , то есть B(7;106);
точка , то есть C(12; 118,3);
точка , то есть D(17; 130,9);
точка , то есть E(22; 133,3).
Нетрудно видеть, что связь между X и Y является линейной. Поэтому уравнение регрессии ищем в виде: .
2) По известным формулам находим числовые характеристики:
Находим и :
3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определим для полной задачи :
Тогда
Уравнение прямой регрессии Y на X имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле
Тогда получаем следующее уравнение регрессии Y на X:
Составим теперь уравнение регрессии X на Y:
.
Построим прямые регрессий и .
|
|
Задача № 1
Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников, 7 студентов третьего курса. Из этого состава выбирают 5 человек. Найти вероятность того, что:
- все первокурсники попадут в совет;
- в совет будет избран 1 первокурсник, 2 второкурсника, 2 студента третьего курса.
Решение
Общее число различных вариантов выбора пяти человек из данных (3+5+7)=15-ти человек:
1) Число различных вариантов выбора пяти человек, когда все три первокурсника попадут в совет:
Вероятность того, что все первокурсники попадут в совет:
2) Число различных вариантов выбора пяти человек, когда в совет будут выбраны 1 первокурсник, 2 второкурсника и 2 студента 3-го курса:
Соответствующая вероятность:
Ответ: 1) 0,0220; 0,210.
Задача № 11
Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки в первое отделение равна 0,95, во второе — 0,9, в третье — 0,8. Найти вероятность того, что хотя бы одно отделение получит газеты вовремя.
Решение
Пусть pi – вероятность своевременной доставки газеты в i-ое отделение, i=1,2,3. Тогда вероятность того, что в i-ое отделение газета не будет доставлена вовремя: qi = 1 – pi.
Вероятность того, что ни в одно отделение газеты не будут доставлены вовремя:

Искомая вероятность того, что хотя бы одно отделение получит газеты вовремя:

Ответ: 0,999.
Задача № 23
Три автомата изготавливают однотипные детали, которые поступают на общий конвейер. Производительности первого, второго и третьего автомата соотносятся как 2 : 3 : 5. Вероятность того, что деталь с первого автомата – высшего качества, равна 0,9, для второго – 0,8, для третьего – 0,6. Найти вероятность того, что:
- наугад взятая с конвейера деталь окажется высшего качества;
- взятая наугад деталь высшего качества изготовлена 2-м автоматом.
Решение
Пусть Н1 = {Деталь изготовлена 1-м автоматом}, H2 = {Деталь изготовлена 2-м автоматом}, H3 = {Деталь изготовлена 3-м автоматом}, A = {Деталь высшего качества}. По условию имеем вероятности:
1) По формуле полной вероятности находим вероятность того, что наугад взятая с конвейера деталь окажется высшего качества:
2) Пусть взятая с конвейера деталь оказалась высшего качества.
Тогда вероятность того, что она изготовлена вторым автоматом (по формуле Байеса):
Ответ: 1) 0,72; 2) 0,333.
Задача № 39
В партии 20% нестандартных деталей, т.е. вероятность появления нестандартных деталей одинакова и равна р = 0,2. Наудачу отобраны 4 детали. Определить ряд распределения, построить многоугольник распределения, функцию распределения случайной величины Х — числа нестандартных деталей среди четырех отобранных. Найти математическое ожидание и дисперсию.
Решение
Возможные значения СВ Х: 0; 1; 2; 3; 4.
Находим соответствующие вероятности по формуле Бернулли:

Строим ряд распределения СВ Х.
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
Проверка:

Строим многоугольник распределения.

Функция распределения:

Строим график функции распределения.

Для определения числовых характеристик СВ Х составим расчётную таблицу.
xi |
pi |
xipi |
|
0 |
0,4096 |
0 |
0 |
1 |
0,4096 |
0,4096 |
0,4096 |
2 |
0,1536 |
0,3072 |
0,6144 |
3 |
0,0256 |
0,0768 |
0,2304 |
4 |
0,0016 |
0,0064 |
0,0256 |
∑ |
1 |
0,8 |
1,28 |
Математическое
ожидание:

Дисперсия:


Задача № 41
Приводятся результаты наблюдений (xi, yi) над двумерной величиной (Х, Y). Используя эти экспериментальные данные, необходимо:
1) построить корреляционное поле. По характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости Y от X и X от Y;
2) определить числовые характеристики ;
3) написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
4) вычислить коэффициент корреляции.
x y |
10 |
20 |
30 |
40 |
ny |
20 |
1 |
|
|
|
1 |
40 |
4 |
1 |
|
|
5 |
60 |
1 |
15 |
1 |
|
17 |
80 |
|
2 |
13 |
|
15 |
100 |
|
|
2 |
1 |
3 |
120 |
|
|
|
9 |
9 |
nx |
6 |
18 |
16 |
10 |
n = 50 |
Решение
По данной таблице находим координаты экспериментальных точек:
Строим корреляционное поле по найденным точкам.
D
C
B
A
По расположению точек на корреляционном поле видно, что связь между X и Y является линейной. Поэтому уравнение регрессии Y на X следует искать в виде: Y = aX + b.
Для определения числовых характеристик двумерной случайной величины составим расчётную таблицу.
X |
nx |
Xnx |
X2nx |
Y |
ny |
Yny |
Y2ny |
10 |
6 |
60 |
600 |
20 |
1 |
20 |
400 |
20 |
18 |
360 |
7200 |
40 |
5 |
200 |
8000 |
30 |
16 |
480 |
14400 |
60 |
17 |
1020 |
61200 |
40 |
10 |
400 |
16000 |
80 |
15 |
1200 |
96000 |
∑ |
50 |
1300 |
38200 |
100 |
3 |
300 |
30000 |
|
|
|
|
120 |
9 |
1080 |
129600 |
|
|
|
|
∑ |
50 |
3820 |
325200 |
Числовые характеристики выборки:
Выборочный коэффициент линейной корреляции:
Уравнение прямой линии регрессии Y на Х:
Уравнение прямой линии регрессии X на Y:
Строим линии (1) и (2) и экспериментальные точки.
D
C
B
Вариант 09
Задание 1.
Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников, и 7 студентов третьего курса. Из этого состава выбирают 5 человек. Найти вероятность того, что:
•все первокурсники попадут в совет;
•в совет будет избран 1 первокурсник, 2 второкурсника,
2 студента III курса.
Решение
Пусть событие А состоит в том, что все первокурсники попадут в совет. Вероятность события А найдем по классическому определению вероятности :
Р(Б)=
m= =
= =3003
=3003
Выбрать
трех первокурсников из трех можно одним
способом. Оставшихся двух членов совета
можно выбрать
 способам:
способам:
= =66
=66
Искомая вероятность p=66/3003=2/91.
Задание 11.
Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки в первое отделение равна 0,95, во второе — 0,9, в третье — 0,8. Найти вероятность того, что хотя бы одно отделение получит газеты вовремя.
Решение:
Р( )=0,95;
Р(
)=0,95;
Р( )=0,9;
Р(
)=0,9;
Р( )=0,8
)=0,8
Вероятность того, что хотя бы одно отделение получит газеты вовремя :
Р(Y)=Р(
 =Р(
)*Р(
)*Р(
)=0,95*0,9*0,8=0,684.
=Р(
)*Р(
)*Р(
)=0,95*0,9*0,8=0,684.
Задание 25.
В дисплейном классе имеется 10 персональных компьютеров первого типа и 25 — второго. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,95, а на компьютере второго типа — 0,8. Найти вероятность того, что:
• на случайно выбранном компьютере за время работы не произойдет сбоя;
• компьютер, во время работы на котором не произошло сбоя, - второго типа.
Решение:
Обозначим А- событие, состоящее в том, что за время работы не произойдет сбоя. Можно выдвинуть две гипотезы:
 выбран компьютер
первого типа
выбран компьютер
первого типа
 выбран компьютер
второго типа
выбран компьютер
второго типа
Вероятности гипотез:


Условная вероятность того, что на компьютере первого типа не произойдет сбой

На компьютере второго типа не произойдет сбой

Вероятность события А найдем по формуле полной вероятности


Вероятность того, что компьютер, во время работы на котором не произошло сбоя, - второго типа найдем по формуле Байеса

Ответ:


Задание 31.
Дана дискретная случайная величина Х. Построить: 1) ряд распределения; 2) многоугольник распределения; 3) функцию распределения F(x). Рассчитать: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение. Из урны содержащей 5 белых и 3 черных шара, наугад извлекают 4 шара. Х — число вынутых белых шаров.
Решение.
Случайная величина Х- число вынутых белых шаров может принимать значения : 1,2,3,4. Найдем вероятности каждого значения Х, для этого воспользуемся классическим определением вероятности




Ряд распределения
x |
1 |
2 |
3 |
4 |
p |
|
|
|
|
Многоугольник распределения
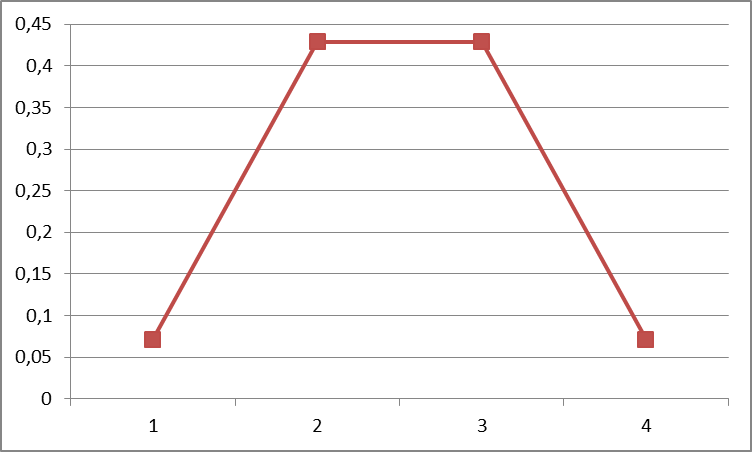
Функция распределения


Вычисляем математическое ожидание и дисперсию:


D[x]
=
 - (2,5)2
= 0,536.
- (2,5)2
= 0,536.
Среднее квадратическое отклонение

Задание 49.
Приводятся результаты наблюдений над двумерной случайной величины (X,Y). Используя эти экспериментальные данные, необходимо:
1) построить корреляционное поле. По характеру расположения точек на корреляционное поле подобрать математическую модель регрессионной зависимости Y от X и X от Y (рекомендуется использовать модель линейной регрессии);
2) определить числовые характеристики ;
3) написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
4) вычислить коэффициент корреляции.
x |
2 |
7 |
12 |
17 |
2 |
27 |
ny |
y |
|||||||
100 |
2 |
4 |
|
|
|
|
6 |
110 |
|
6 |
2 |
|
|
|
8 |
120 |
|
|
3 |
50 |
2 |
|
55 |
130 |
|
|
1 |
10 |
6 |
|
17 |
140 |
|
|
|
4 |
7 |
3 |
14 |
nx |
2 |
10 |
6 |
64 |
15 |
3 |
n = 100 |
Решение.
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D, E, F.
Точка А имеет координаты , где , , то есть ;
точка , то есть B(7; 106);
точка , то есть C(12; 118,89);
точка , то есть D(17; 12,81);
точка , то есть E(22; 133,33).
.
Нетрудно видеть, что связь между X и Y является линейной. Поэтому уравнение регрессии ищем в виде: .
2) По известным формулам находим числовые характеристики:


Находим и :


3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определим для полной задачи :

Тогда

Уравнение прямой регрессии Y на X имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле
Тогда получаем следующее уравнение регрессии Y на X:
Составим теперь уравнение регрессии X на Y:
.


Построим прямые регрессий и .

Задача 6
6. Среди 50 фотокарточек есть одна фотокарточка знаменитого артиста. Взяли наудачу 10 фотокарточек. Какова вероятность того, что среди них есть фото артиста?
Решение
Пусть событие А - событие, при котором происходит выбор 10 фотокарточек, причем одна из них является фотокарточкой знаменитого артиста. Вероятность события А находится по классическому определению вероятности
,
где m — число равновозможных элементарных событий, благоприятных для события А, т. е. для задачи 1 m — это число способов, которыми можно выбрать 1 фотокарточку знаменитого артиста из 10 имеющихся, предварительно выбранных карточек.
Так как порядок выбора не имеет значения, то
 ;
;
n — число всех возможных элементарных событий, то есть в задаче 1 n — это число способов, которыми можно выбрать 10 фотокарточек из 50 имеющихся.
Так как порядок отбора не имеет значения, то
 .
.
Таким образом,
 .
.
Отчет: Вероятность того, что среди взятых наудачу 10 фотокарточек будет фотокарточка знаменитого артиста составляет 0,00000000097.
Задача 11
11. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки в первое отделение равна 0,95, во второе — 0,9, в третье — 0,8. Найти вероятность того, что хотя бы одно отделение получит газеты вовремя.
Решение
Пусть событие А1 состоит в том, что газеты дошли вовремя в первое отделение, А2 – во второе и А3 –в третье отделение.
Тогда событие В состоит в том, что хотя бы одно отделение получит газеты вовремя, является суммой трех совместных событий А1, А2 и А3, то есть либо одно из трех отделений получит газеты вовремя, либо два из трех, либо все три отделения получат газеты вовремя.
По теореме сложения вероятностей трех совместных событий получим уравнение:
 .
.
А так как
,
и —
независимые события, то для них верно:
—
независимые события, то для них верно:

Ответ: Вероятность доставки газет хотя бы в одно отделение вовремя равна 0,999.
Задача 21
21. На предприятии 30% приборов монтируется с применением микромодулей, остальные — с применением интегральных схем. Надежность прибора с применением микромодулей — 0,9, интегральных схем — 0,85. Найти:
вероятность надежной работы наугад взятого прибора;
вероятность того, что прибор был монтирован с интегральной схемой, если он исправен.
Решение
Пусть
A
- событие,
при котором наугад взятый прибор надежен.
Через
 обозначает
событие, при котором взятый прибор
является микромодульным, а через
обозначает
событие, при котором взятый прибор
является микромодульным, а через
 - интегральным. Тогда
,
- интегральным. Тогда
,
 ,
,
 ,
,
 .
По формуле полной вероятности вероятность
надежной работы случайно выбранного
прибора выражается формулой:
.
По формуле полной вероятности вероятность
надежной работы случайно выбранного
прибора выражается формулой:

Для ответа на второй вопрос поставленной задачи необходимо воспользоваться формулой Байеса. Для данного случая она будет выглядеть следующим образом:
 .
.
Ответ:
1) Вероятность исправной работы наугад взятого прибора составляет 0,865.
2) Вероятность того, что исправный прибор монтирован с интегральной схемой, составляет 0,688.
Задача 36
36. Стрелок трижды стреляет в мишень. Вероятность промаха при одном выстреле равна 0,1. Построить многоугольник распределения, закон и функцию распределения случайной величины Х — числа промахов при 3 выстрелах. Найти математическое ожидание и дисперсию Х.
Решение
Так как вероятность
того, что стрелок промахнется, стреляя
по мишени, постоянна
 и не зависит от исходов предыдущих
выстрелов, то случайная величина Х
— числа промахов, подчиняется биномиальному
закону распределения, т.е. Х
= 0, 1, 2, 3, а
(в соответствии с формулой Бернулли).
и не зависит от исходов предыдущих
выстрелов, то случайная величина Х
— числа промахов, подчиняется биномиальному
закону распределения, т.е. Х
= 0, 1, 2, 3, а
(в соответствии с формулой Бернулли).
Найдем соответствующие вероятности:




Исходя из выше найденных величин, ряд распределения случайной величины Х будет выглядеть следующим образом:
Х |
0 |
1 |
2 |
3 |
Р |
0,729 |
0,243 |
0,027 |
0,001 |
Многоугольник распределения дискретной случайной величины Х будет выглядеть так, как представлено на графике:

Вычислим математическое ожидание случайной величины Х:


Далее рассчитаем значение дисперсии:


Среднее квадратическое отклонение, исходя из значения дисперсии, будет равным:
 .
.
Задача 44
Приводятся результаты наблюдений над двумерной случайной величины . Используя эти экспериментальные данные, необходимо:
построить корреляционное поле, по характеру расположения точек на корреляционном поле подобрать математическую модель регрессионной зависимости Y на X и X на Y (рекомендуется использовать модель линейной регрессии).
определить числовые характеристики выборки ;
написать выборочные уравнения прямых линий регрессии Y на X и X на Y и построить их графики;
вычислить коэффициент корреляции.
x |
0,75 |
0,80 |
0,85 |
0,90 |
ny |
y |
|||||
10 |
6 |
|
|
|
6 |
20 |
4 |
2 |
|
|
6 |
30 |
|
12 |
|
|
12 |
40 |
|
6 |
4 |
1 |
11 |
50 |
|
|
6 |
9 |
15 |
nx |
10 |
20 |
10 |
10 |
n = 50 |
Решение
1) Для предварительного установления зависимости X и Y по данным таблицы построим корреляционное поле в системе координат .
Определяем координаты точек A, B, C, D.
Точка А
имеет координаты
,
где
 ,
,
 ,
то есть
,
то есть
 ;
;
точка
 ,
то есть B(0,8;
32);
,
то есть B(0,8;
32);
точка
 ,
то есть C(0,85;
46);
,
то есть C(0,85;
46);
точка
 ,
то есть D(0,9;
49);
,
то есть D(0,9;
49);
Тогда корреляционное поле будет выглядеть следующим образом:

Исходя из представленного выше корреляционного поля, можно сказать, что связь между X и Y является линейной. Поэтому уравнение регрессии в общем виде будет иметь вид: .
2) По известным формулам находим числовые характеристики:


Определяем значения и :




3) Для того, чтобы написать выборочные уравнения прямых линий регрессии, необходимо найти коэффициент линейной корреляции по формуле
Определяем значение :


Тогда

4) Уравнение прямой регрессии Y на X в общем виде имеет вид
,
где — коэффициент регрессии Y на X, который находится по формуле

Тогда получаем следующее уравнение регрессии Y на X:

По аналогии составим уравнение регрессии X на Y:
.


Построим прямые
регрессий
 и
и
 .
.
|
|









