9 Примеры решения типовых задач

9.1 Последовательность решения задач

1. Изучить условие задачи. Заданные изображения элементов геометрических фигур пропорционально увеличить в 2…2,5 раза, чтобы получить более четкое решение.

2. Задачу решить сначала «в пространстве». По чертежу в проекциях студент должен представить себе форму и расположение заданных геометрических элементов и установить последовательный порядок построений в пространстве, при помощи которых находятся искомые элементы задачи.

3. Составить и записать план решения.

4. Выполнить графические построения на чертеже, отражающие план решения.

5. Выполнить анализ полученного решения (отвечает ли оно последовательному условию задачи), а также анализ на множество возможных искомых решений.

9.2 Примеры решения

9.2.1 На комплексном чертеже.

Задача 1 Определить углы наклона плоскости, заданной треугольником ABC, к плоскостям проекций П₁ и П₂ (рисунок 9.1).

План решения:

1. Проводим проекции горизонтали и фронтали плоскости.

2. Проводим проекции линии ската и линии уклона плоскости.

3. Находим натуральную величину линий ската и уклона.

4. Применяя метод прямоугольного треугольника определяем углы наклона  и  плоскости ABC к плоскостям проекций.

На рисунке 9.1 показано решение задачи.

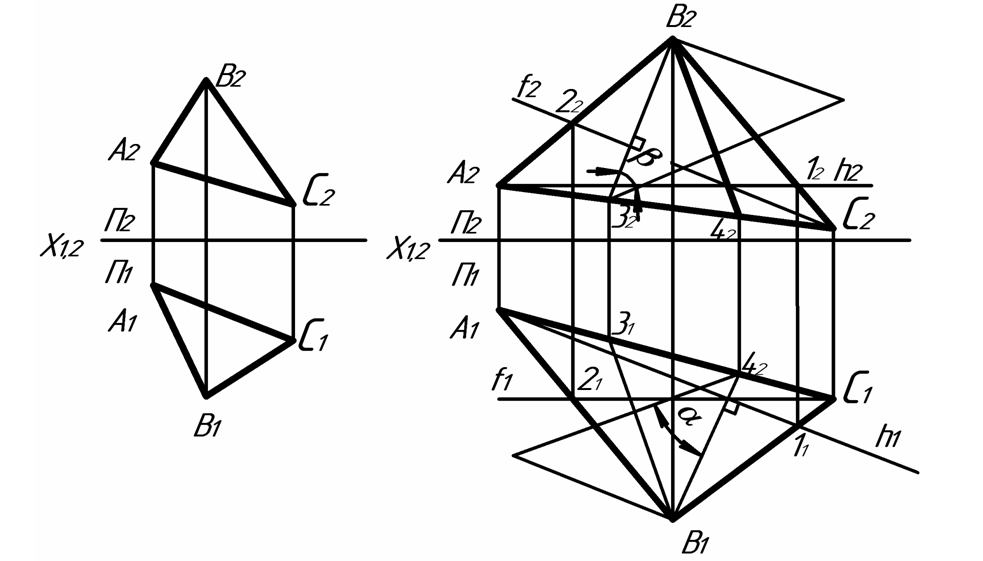
а) б)

Рисунок 9.1 Пример решения задачи на комплексном чертеже:

а – условие задачи; б – решение задачи.

Задача 2 Определить угол наклона прямой АВ к плоскости Г( ) (рисунок 9.2).

Решение: Находим точку пересечения прямой АВ с плоскостью Г.(рисунок 9.2а)

Рисунок 9.2

Рисунок 9.2а

Так как угол между плоскостью и прямой измеряется углом между самой прямой и ее проекцией на данную плоскость, то для получения проекции из точки А опускаем перпендикуляр ев плоскость и находим точку пересечения его с плоскостью (рисунок 9.2б). прямая КС есть проекция прямой АК на плоскости Г

Рисунок 9.2 б

Рисунок 9.2в

Зная, что в прямоугольном треугольнике сумма двух острых углов равна 90⁰, находим натуральную величину угла при вершине А и к нему строим дополнительный угол до 90⁰, который будет равен искомому углу при вершине К. этот угол находится путем вращения его вокруг горизонтали 5-6(рисунок 9.2в).

9.2.2 В проекциях с числовыми отметками.

Задача 1. Через точку М, лежащую на прямой А₆ В₂ , провести горизонтальную прямую МN так, чтобы она пересекалась с данной прямой С₃ D₈ . (рисунок 9.3).

Рисунок 9.3

Рисунок 9.3а

Решение:

Градуируем прямую А₆ В₂ и определяем отметку точки М, она равна 4,3 (рисунок 9.3а).

Градуируем прямую С₃ D₈ и находим на ней точку с той же отметкой 4,3. Это и будет искомая точка N (рисунок 9.3б).

Рисунок 9.3б

Рисунок 9.3в

Соединяя точку М с N, получаем искомую горизонтальную прямую МN (рисунок 9.3в).

Задача 2..Определить угол наклона (падения) плоскости, заданной треугольником АВС, к горизонтальной плоскости проекций. На чертеже показать направление и угол простирания плоскости А₂В₉С₇.(рисунок 9.4)

Рисунок 9.4

Рисунок 9.4а

Решение: Градуируем сторону треугольника с наибольшей разностью отметок А₂В₉ (рисунок 9.4а).

Рисунок 9.4б

Рисунок 9.4в

Проводим горизонтали плоскости, для чего соединяем точки С₇. и 7, а через точки 3, 4, 6, 8, 9 проводим линии, параллельные С₇ и 7. Это будут горизонтали плоскости (рисунок 9.4б) Здесь же проводим линию масштаба уклона перпендикулярно горизонталям плоскости.

Находим угол наклона плоскости, для чего от точки 2 откладываем ΔZ=7 масштабным единицам и полученную точку соединяем с точкой 9 на линии масштаба уклона. Угол α будет искомым (рисунок 9.4в).

Рисунок 9.4г

Угол между правым напрвлениемгоризонталей, если смотреть в сторону возрастания отметок и северным направлением магнитной стрелки является углом простирания плоскости (рисунок 9.4г).

Задача 3. Построить линию пересечения плоскостей, каждая из которых задана прямой, уклоном и направление падения (рисунок 9.5)

Решение: Градуируем прямые А₄В₉ и С₄D₇ (рисунок 9.5а)

Рисунок 9.5

Рисунок 9.5а

Через точки 4, 5, 6, 7 и 8 прямой АВ и через точки 4, 5, 6, 7 на прямой СD проводим основания конусов радиусами, равными интервалам заданных плоскостей 1:1 и 1:2 (рисунок 9.5б)

Рисунок 9.5б

Рисунок 9.5в

Через точки 4, 5, 6, 7, 8 на прямой АВ и через точки 4, 5, 6, 7 на прямой СD проводим касательные линии к окружностям. Это будут горизонтали плоскостей (рисунок 9.5в) Пересечение горизонталей с одинаковыми отметками дадут линию пересечения плоскостей Р₄Т₇.