26. Представление об организации радиодоступа к общим ресурсам.

Существует дифференциация по виду функционала и виду оператора разделения , они м/б:

- линейными;

- нелинейными.

Возможны след. вар-ты упл-я и разд-я каналов:

- Л упл//разд.

-Н упл//разд.

Возможны любые их сочетания (например, лин упл. – нелин. разд. и т.п.)

В реальной жизни, при Л уплотнении Н разделение бессмысленно, т.к. формируется только линейная зависимость между элементами, и нелинейное разделение ничего не добавляет, по сравнению с линейным.

При Н уплотнении Л разделение возможно, хотя качество его будет хуже.

Коллективный доступ (системы с кодовым У и Р каналов).

Пример такого доступа может служить WiFi.

В таких системах в качестве адресного признака используются различные варианты радиосигналов, при этом эти сигналы используются как несущие сигналов для каждого из источников. Эти сигналы не гармонические, а сложные (кодовые сигналы), состоящие из совокупности ВЧ-радиоимпульсов. Каждый такой сигнал является адресным признаком источника. Введение адресного признака осущ-ся путем модуляции инф. Сигнала соответствующим несущим сигналом.

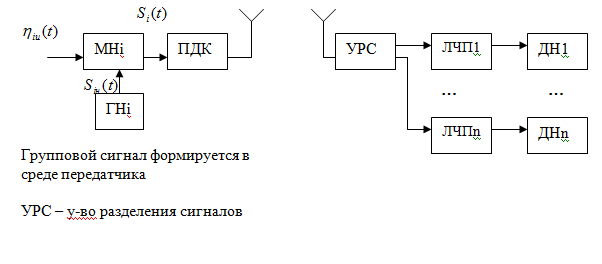
+ см. вопрос 25.

27. Представление об уменьшении логической избыточности в процессе кодирования источника.

Уменьшение логической избыточности - эффективная передача речевых сообщений или речевых сигналов

Для прямой (непрерьвной) передачи речевого сигнала с сохранением разборчивости по содержанию достаточно 3 кГц

С точки зрения разборчивости сточки логической избыточности передачи энергетический спектр (то, что нам необходимо, а не множество побочных звуков).

Методы выравнивания неравновероятных символов

Статистическое кодирование

Первоначальные символы - неравномерное представление кодовыми словами переменной длины Длина кодового слова для каждого символа выбирается обратно пропорционально вероятности появления.

Восьмеричный алфавит. Упорядочим буквы в порядке убывания вероятности появления символов

Используй значение энергетического спектра как воспроизвести речевой сигнал?

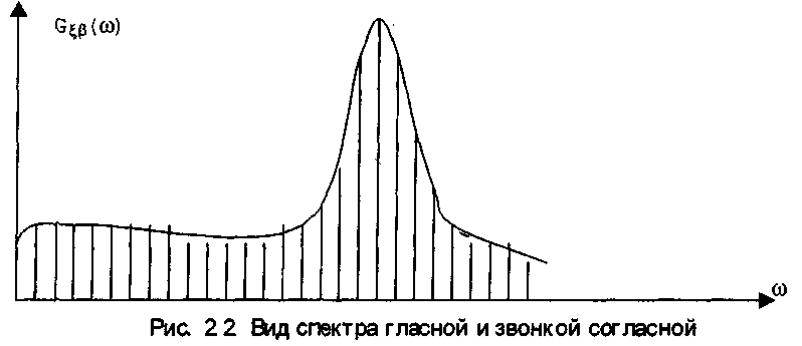
28. Уменьшение статистической избыточности в процессе кодирования источника.

Статистическая избыточность - значения параметра и первичного сигнала распределены неравновероятно.

Существует два метода уменьшения стат. избыточности:

уменьшение зависимости между символами

выравнивание вероятностей символов

Уменьшение зависимости между символами – осуществляется совместно с временной дискретизацией:

экстраполяция

интерполяция

Методы выравнивания неравновероятных символов

Статистическое кодирование

Первоначальные символы - неравномерное представление кодовыми словами переменной длины Длина кодового слова для каждого символа выбирается обратно пропорционально вероятности появления

Восьмеричный алфавит. Упорядочим буквы в порядке убывания вероятности появления символов

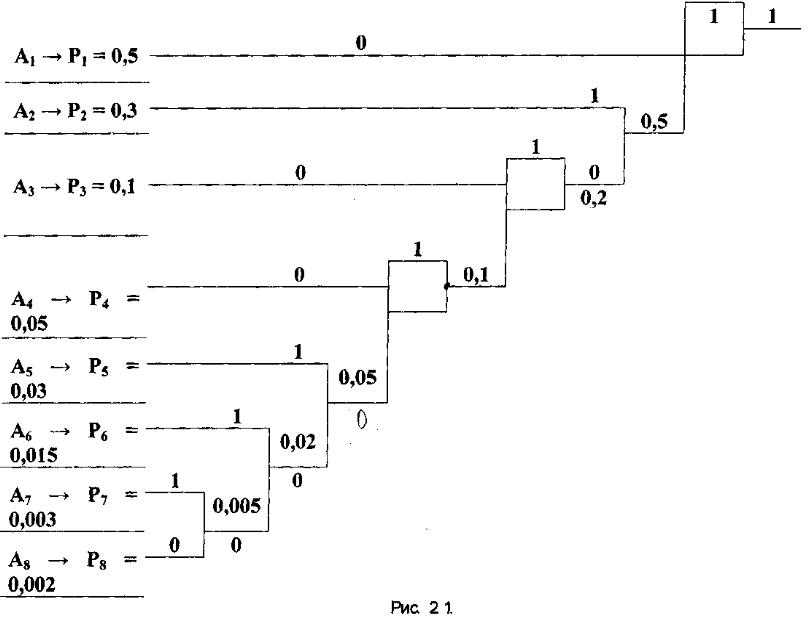
Строится дерево кода от ветвей корня

А8: 0001101

А7: 1001101

А6: 101101

...

А1: 0

Метод кодирования длинных серий с одинаковой длиной (другой метод).

29. Процессы экстраполяции и интерполяции при кодировании источника.

Экстраполяция:

В силу инерционности источника между символами существуют статистические зависимости. Если она есть, то в каждом значении есть часть сведений об остальных. Предположим, что несколько значений первичного сигнала уже переданы. Т.к. в каждом из них содержится часть сведений об остальных.

Предположим, что несколько значений первичного сигнала уже переданы. Т.к. в каждом из них содержится часть сведений обо всех последующих, то, извлекая их, можно с какой-то точностью их предсказать. Предсказание будет с ошибкой. Чем дальше удаляться, тем больше ошибка.

На некотором интервале (ошибка предсказания) может быть несущественной для потребителя.

Таким образом, в декодере источника первичный сигнал может быть восстановлен на интервале без дополнительных значений в требуемом качестве.

Переданные ранее значения могут храниться в памяти кодера и декодера. По ним в кодере источника формируют предсказание последующих значений и, пока ошибка предсказания удовлетворяет потребителя, следующих значений не передают. В декодере источника по тому же алгоритму предсказывают значения и их предоставляют потребителю.

Чем больше используется значений для предсказания, тем предсказание точнее, следовательно, тем длиннее . С другой стороны, чем быстрее процесс изменяется, тем при том же числе значений точность предсказаний будет меньше.

Таким образом, интервал временной дискретизации зависит от:

числа используемых предшествующих значений

скорости изменения состояния источника (то есть изменения )

Чаще всего используется полиномиальное предсказание, то есть используется представление дифференциальной функции в виде полиномиального ряда в окрестности некоторой точки:

где - интервал между исходной точкой и прогнозируемой точкой.

Экстраполяция нулевого порядка:

Ошибка экстраполяции (предсказания) = п – она сравнивается с допустимой величиной :

Восстанавливается экстраполяцией такой сигнал:

Производные заменяются конечными разностями:

, если - достаточно малое (стремиться к нулю),

(пр) – приближенное значение.

В реальных системах используются предсказатели в основном нулевого и первого порядков. (Первого порядка – то есть используется 2 первых члена.) Это связано с тем, что требуемая точность предсказания высока, значит, апертура предсказания мала, интервалы малы. Поэтому использование большего числа членов дает уменьшение статистических зависимостей, но усложняется алгоритм, а выигрыш не столь велик.

Предсказатель работает в реальном времени. В декодере источника первичный сигнал восстанавливается в реальном масштабе времени.

Интервал дискретизации переменный, поэтому экстраполятор – адаптивный временной (в зависимости от скорости изменения или, что то же самое, от ширины спектра).

Интерполяторы

Для интерполяции значений используют сведения из других значений не только из предшествующих, но и из последующих значений (в отличие от экстраполяции).

Это устройства временной дискретизации (такие как экстраполяторы), таким образом, получаем дискретные значения , отстоящие на (зависят от скорости изменения первичного сигнала). На выходе кодера источника получаются в цифровом виде дискретные значения.

Первичный сигнал на выходе кодера источника чаще всего представляется не своими значениями, а множеством значений коэффициентов ряда, которым интерполируется первичный сигнал. дискретизируется по времени:

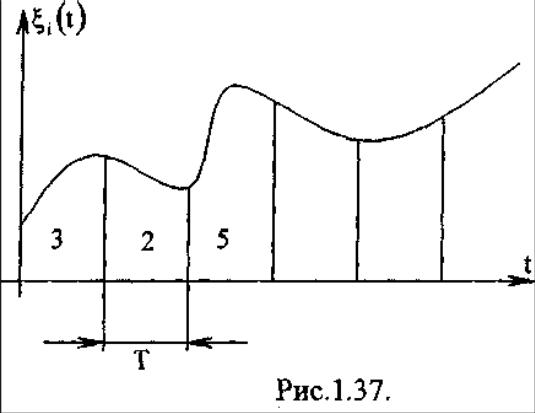
время передачи сигнала разбивается на какие-то интервалы

На каждом из этих интервалов отрезок первичного сигнала представляется каким-то рядом:

Чаще всего используется полиномиальный ряд: и - степенные функции, – требуемое число членов ряда (нужно их определить), - требуется определить значения коэффициентов.

Определяем таким образом, чтобы разность была приемлемой для потребителя:

В декодере источника известны тип ряда . должно быть передано, также как и . Желательно так осуществить интерполяцию, чтобы либо количество членов ряда (и, следовательно, количество передаваемых ) было бы минимальным при фиксированном интервале интерполяции, либо чтобы при фиксированном числе членов ряда интервал временной дискретизации был наиболее возможным. В соответствии с этим различают 2 реализации интерполятора:

1) - интервал дискретизации

Ищется такое минимальное , при котором на еще гарантированно выполняется неравенство .

Таким образом определяется минимальное число членов ряда и вычисляется соответствие коэффициентов . Эти коэффициенты и представляют собой первичный сигнал на этом интервале, поступают на вход кодера источника и передаются. В декодере источника они используются для приближенного воспроизведения интерполяционного ряда.

Вначале надо накопить значения, поэтому интерполятор не позволяет работать в реальном времени, так как после накопления следует анализ для выбора . Так появляется запаздывание на . зависит от скорости изменения первичного сигнала (чем она больше, тем больше требуемое ). Т.е. кол-во передаваемых коэффициентов зависит от скорости изменения .

2) фиксируется . .Тогда в процессе интерполяции определяется максимальное , на котором это число членов ряда еще позволяет удовлетворить требования по точности: .

Количество передаваемых коэффициентов будет таким же, а будет меняться и зависеть от скорости изменения .

Интерполятор полиномиальный первого порядка

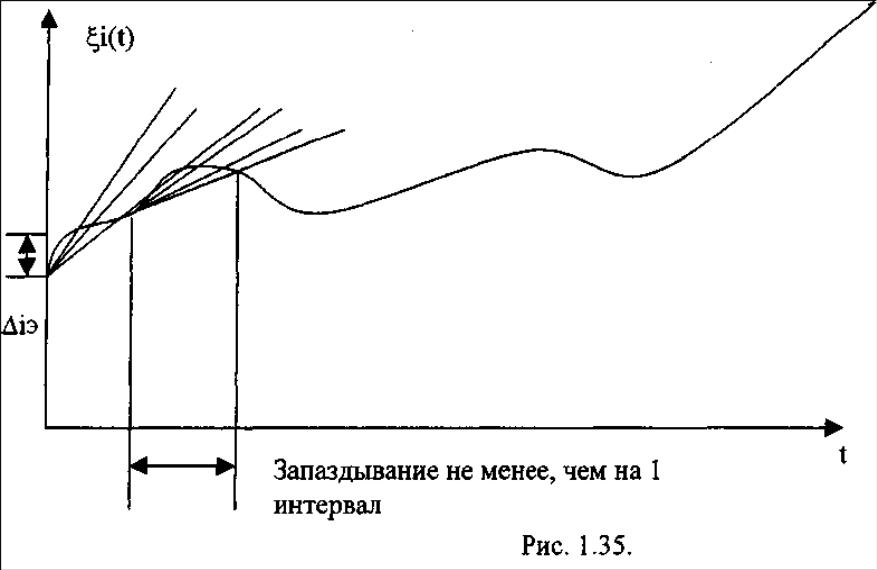
1) всегда передается

2) далее методом проб берется интервал, интерполируются на нем через 2 крайние точки и находится ошибка. Если она достигла значения апертуры интерполяции и передается значение коэффициента. Если не достигла – выбирается другой интервал.

Далее все повторяется.

Таким образом, интерполяторы и экстраполяторы в сочетании с квантованием по уровню дают на выходе с требуемой точностью приближенное представление со значительно уменьшенными статистическими зависимостями. Но вероятности символов последовательности не выровнены.