17. Екі сигналдың өзара корреляцияланған функциясы.

. 

    формуласын жалпылай отырып оны екі сигналдың U(t) және V(t) скалярлық  туындысын өзара корреляциялық функциясы (ӨКФ) деп атап, келесі түрде аламыз:

             .                                   (5.7)

Егер (5.7) формуласындағы интегралдаушы айнымалыны х = t-τ  деп ауыстырып, dt=dx деп алатын болсақ, онда келесі өрнекті аламыз.

            .                                  (5.8)

Сондықтан :

             .                                           (5.9)

Жалғыз сигналдың автокорреляциялық функциясының ӨКФ-дан айырмашылығы екі бірдей емес сигналдар жүйесінің сипатталатын қасиеті  аргументінің  жұп функциясы болып табылмайды:

B_uν(τ) ≠. B_uν(-τ)

Егер қарастырылатын сигналдардың ақырғы энергиялары болса, онда өзара корреляциялық функция шектелген. Бұл мақұлдылық Коши-Бунянковский теңсіздігінен шығады:

.

Бұл жерде,

                                 .                            (5.10)

Себебі уақыт бойынша сигнал ығысуы оның нормасының мәніне әсер етпейді.

Мынаған назар аударған жөн, егер  τ=0  болғанда ӨКФ-нің мәні максимумға жету тиіс емес.

18.Кейбір өзара корреляцияланған функциялардың сипаттары (қасиеттері).

. 

    формуласын жалпылай отырып оны екі сигналдың U(t) және V(t) скалярлық  туындысын өзара корреляциялық функциясы (ӨКФ) деп атап, келесі түрде аламыз:

             .                                   (5.7)

Егер (5.7) формуласындағ интегралдаушы айнымалыны х = t-τ  деп ауыстырып, dt=dx деп алатын болсақ, онда келесі өрнекті аламыз.

            .                                  (5.8)

Сондықтан :

             .                                           (5.9)

Жалғыз сигналдың автокорреляциялық функциясының ӨКФ-дан айырмашылығы екі бірдей емес сигналдар жүйесінің сипатталатын қасиеті  аргументінің  жұп функциясы болып табылмайды:

.

Егер қарастырылатын сигналдардың ақырғы энергиялары болса, онда өзара корреляциялық функция шектелген. Бұл мақұлдылық Коши-Бунянковский теңсіздігінен шығады:

.

Бұл жерде,

                                 .                            (5.10)

Себебі уақыт бойынша сигнал ығысуы оның нормасының мәніне әсер етпейді.

Мынаған назар аударған жөн, егер  τ=0  болғанда ӨКФ-нің мәні максимумға жету тиіс емес.

19 Өзара корреляцияланған функциялардың өзара спектрлі тығыздығымен байланысы.

Спектральді сипаттамалар арқылы екі сигналдық ӨКФ-н өрнектейік.

Рэлея формуласына негізделе отырып :

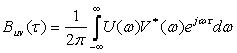 аламыз.

 шамасы сигналдың U(t) және V(t) өзара энергетикалық спектр екенін ескере отырып, шексіз жиіліктер интервалында -∞<ω<∞ анықталған, мынадай шешімге келеміз: Өзара корреляциялық функция және екі сигналдың өзара энергетикалық спектрі Фурье түрлендіруінің жұбымен байланысты.

20.Кездейсоқ процесс түсінігі

Жалпы байланыс теориясын зертттеу тәсілдерінің негізінде, уақыт бойынша дамитын кейбір кездейсоқ процесс ретіндегі хабарды тарату процессі жөніндегі көрсетілу жатыр. Кездейсоқ  сөзі алдын-ала процестің нақты таралуын болжау мүмкін еместігін көрсетеді. Анықтау бойынша кездейсоқ процесс X(t)-бұл кез-келген t уақыт мезетінде қабылданатын мәндер кездейсоқ шамалар болып табылатын ерекше түрдегі функция. Кездейсоқ процесстің типтік мысалы ретінде қабылдағыш кірісінде Z(Q)=S(t)+N(t) кернеуі жұмыс жасай алады. Берілген мезетте кернеуді бақылай отырып, біз келесі уақыт мезеттерінде ол қандай мәнлерге ие бола алатындығын болжай аламыз. Бұл мынамен  түсіндіріледі: таратушымен қалыптастырылатын арналық каналдың S(t) (амплитуда, жиілік, фаза) параметрлері жіберілетін хабарға a(t) байланысты кездейсоқ өзгеріп отырады. Сонымен бірге, таралу процесінде сигнал кездейсоқ сипатқа ие әртүрлі адетивті бөгеуілдердің N (t) әсеріне шалдығады. Мысалы: атмосфера электрлік разряд түрінде,электрлік  транспорттың бөгеуілдері, басқа радиостанциялық бөгеуілдер және т.б. Процестің кездейсоқтылығы X(t) бақыланатын функцияның түрі бір бақылаудан басқасына кездейсоқ ауысатындығымен көрсетіледі. Бірақ, әрбір жеке тәжірибеден алынатын X(t)  функцияның шешімі кездейсоқ емес, оны кездейсоқ функцияның таралуы(реализация)деп аталады. Кездейсоқ процесс статикалық ансамбль жасайтын шексіз мұндай таралулардың жиынтығын ұсынады. 5.1-суретте кездейсоқ процестің төрт таралуы көрсетілген. Егер графиктен кездейсоқ функцияның X (t) көптеген таралулар мезетін таңдасақ, онда көптеген таралу мәндері осы мезетте кездейсоқ шама құрайды. Бұл кездейсоқ шаманың мәндері алдын-ала белгісіз. Бірақ  кейбір заңдылықтарды орнатуға болады. Бұл қимада кездейсоқ шама Р ықтималдықпен шектелген аралықтағы  мәндерді қабылдайды.

         Үзіліссіз процесстер  X(t)  үшін t,берілген қимасындағы ықтималдық тарауы бір өлшемді ықтималдық тығыздығымен сипатталады:

 

5.1 Сурет -Кездейсоқ процестің төрт таралуы	5.2 Сурет -Бір өлшемді ықтималдық тығыздығының типтік графигі

 

Кездейсоқ шама X(t) аралындағы мәндерді қабылдайды.    аралығының шамасына 5.2 а суретте бір өлшемді ықтималдық тығыздығының типтік графигі көрсетілген.

         Кездейсоқ шама (х₁;х₂) аралығында қандай да бір мәнге ие болу ықтималдығы өрнегімен анықталады.

Басқa х шамасынан асып кетпеу ықтималдығымен анықталатын кездейсоқ Х шамасының маңызды сипаттамасы ИФР  F(x) болып табылады.

ИФР келесі қасиеттерге ие:

а) F(-∞)=0;

б) F(∞)=1;

в) F(x) — шығынсыз функция, яғни х₂ > x₁ кезінде F (x₂) ≥ F (x₁);

г) P[x₁≤X≤x₂]=F(x₂)- F(x₁).

Қолданбалы есептерде ИФР дифференциалданатын функция деп есептелінеді және  w(x) ИФР- ден алынған деп туынды деп анықтайды:

.

Кездейсоқ процессті толығырақ сипаттау үшін кездейсоқ процесстің қасиетін сипаттайтын  қималарында  n - өлшемді ықтималдық тығыздығымен  w(x₁, x_2,…, x_n; t₁,t_2,…, t_n)  немесе F(x₁, x_2,…, x_n; t₁,t_2,…, t_n) n - өлшемді ИФР t₁,t_2,…, t_n бойынша орналыстыру керек.

         Уақыт бойынша үзіліссіз СП-ні толық сипаттау үшін п→∞ ұмтылады. Процесс қималарда байқалатын кейбір мезеттер уақыттық аргументтерге тәуелді болады. Олар мезеттік функциялар деп аталады. Статикалық радиотехника үшін төменгі реттегі  3 мезеттік функциялардың маңызы зор. Олар: математикалық күтім, дисперсия және корреляция функциясы деп аталады.