5.Динамикалық көрсету принципі

Динамикалық көрсетудің екі әдісі кеңінен қолданады: біріншісіне сәйкес элементарлы сигналдар ретінде уақыттың тең аралықтары арағындағы пайда болатын, баспалдақты функциялар қолданылады.

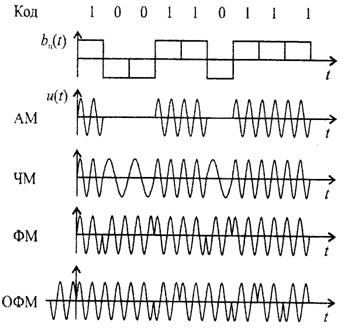
2.3 Сурет - Әр түрлі дискретті модуляция үшін екілік кодтағы сигнал түрлері

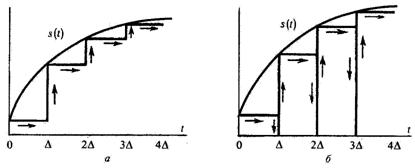
2.4 Сурет - Сигналдардың динамикалық көрсетілу тәсілі

Әрбір баспалдақтын биіктігі уақыт интервалында сигналдың өзіне алып келеді. Екінші әдіс кезінде элементарлы сигналдар болып тік бұрышты импульстер қызмет көрсетеді (2.4а суретті қара). Бұл импульстер тікелей бір-бірімен жанасады және қиылысқан немесе оның бойымен сипатталған тізбекті құрайды (2.4б суретті қара). Бірінші әдіс бойынша динамикалық көрсетілім үшін қолданылатын элементарлы сигналдың қасиеттерін қарастырайық:

Егер функция бір физикалық объектінің 0-діктен біріншілік күйіне ауысу процессін сипаттаса шектеулі сигналдың математикалық моделін қосу функциясы немесе Хевисайд функциясы деп атайды: 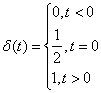                                .   (2.2)

Теориялық радиотехникада қосу функциялары үзілісті жеке алғанда импульсті сигналдарды сипаттау үшін кең қолданылады:

6.Кодтау және модуляция критерияларын (шарттарын)өңдеу

Модуляция қандай да бір стационар физикалық процесті сипаттайтын параметрлердің уақытқа байланысты берілген заңдылық бойынша өзгеруі. Модуляцияның 3 түрі бар: амплитудалық,фазалық,жиіліктік.

АМ-радиотаратқыш тарататын электромагниттік тербеліс амплитудасын сол тербеліс жиілігінен төмен жиіліктегі тербеліс заңына сәйкес өзгерту.

ФМ-тасымалданатын сигнал тасушы жоғары жиілікті тербелістің фазасын басқарады. ФМ жағдайында сигналдың спектрі мен пішіні бірдей болады. Гармоникалық тасушы сигналдың фазасы хабар сигналының заңдылығымен өзгеретін сигналды ФМ д.а. АМ мен ЖМ қарағанда ФМ бөгеуілдерге орнықты, сол себепті оның дәлдігі жоғары болады.

ЖМ-генератор жиілігінің модуляциялаушы кернеу әсерінен өзгеруі. АМ салыстырғанда ЖМ қабылдау кезінде электрлік бөгеуілдер әсерінен төмендете алады.

7.Хабарлардың және сигналдардың математикалық модельдері.

Периодты сигналды и және v ортогональді деп атайды. Егер олардың скалярлық туындысы өзара энергиясы 0-ге тең болса:  (u,v)= u(t)v{t)dt=0.                         (3.1)

Онда Н-энергиясының соңғы мәні бар сигналдардың Гильбертті кеңістігі. Бұл сигналдар ақырғы және шексіздік уақыт кесіндісінде анықталады [t₁t₂]. Бұл кесіндіде шексіз функция берілген: {U₀,U₁,……..U_n} деп болжасақ бір-біріне ортогональды және бірлік нормалары болады:

                     .                             (3.2)

Бұл сигналдар кеңістігінде ортонормаланған базис берілген. Кездейсоқ сигналды  s(t) H қатарына жіктейміз:s(t)= .                                   (3.3)

3.3-көрсетілімі таңдалған Базисте сигналының жалпыланған Фурье қатары деп аталады.

Берілген қатарлардың коэффициентерін келесі жолмен табамыз. Базистер функцияны кездейсоқ нормамен екі теңдігімен интегралдаймыз:

                                                    .                     (3.4)

3.4 теңдігінің оң бөлігінің Базистің ортонормаланғандығын ескерсек қосынды мүшесі қалады, сондықтан:

                                                (3.5)

Енді сигналдарды жалпыланған Фурье қатарының C_k коэффициентін есепті жүйемен сипаттауға болады. Гармоникалық функциялардың ортонормаланған жүйесі: [0,t] кесіндісінде еселенген жиіліктері бар тригонометриялық функциялардың жүйесі тұрақты сигналмен толықтырылған, ортонормаланған Базисті кұрайды: