Выявление сезонной составляющей.

Сезонность – систематически повторяющаяся тенденция во временном ряду.

Предварительно рассмотрим периодограмму для остатков полученной выше модели квадратичного тренда (ВР после вычитания линейного тренда):

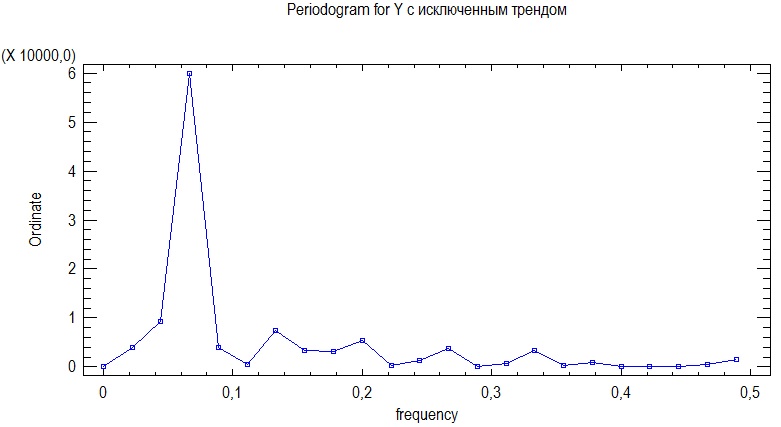
Рисунок 7. Периодограмма для индекса РТС с исключенным значением тренда.

Так же приведем график распределения индекса РТС по месяцам:

Рисунок 8. Индекс РТС по месяцам с исключенным трендом.

От сюда видно, что каких-либо одновременных устойчивых колебаний не присутствует. Однако для большей точности проверим данное утверждение при помощи введения в модель фиктивных переменных. Как видно на периодограмме и соответствующей таблице в приложение самому наибольшему колебанию соответствует период в , т.е. период получается на 3 месяца больше, чем сам год, скорее всего он, был вызван резким ростом индекса после развернувшегося кризиса, поэтому возьмем следующий период колебания .

Введем 7 фиктивных переменных и оценим параметры модели:

		Standard	T
Parameter	Estimate	Error	Statistic	P-Value
CONSTANT	-35,648	27,1209	-1,31441	0,1970
t	0,769897	0,594665	1,29467	0,2037
h1	15,1879	31,277	0,485595	0,6302
h2	19,3145	31,2487	0,61809	0,5404
h3	14,1886	31,2317	0,454301	0,6523
h4	41,2019	31,2261	1,31947	0,1953
h5	45,8309	31,2317	1,46745	0,1509
h6	33,474	32,6362	1,02567	0,3119
h7	23,4731	32,62	0,719592	0,4764

Таблица 10. Оценка параметров модели индекса РТС с исключённым трендом с фиктивными переменными.

Так как все коэффициенты получились не значимы можно сделать вывод о том, что в данном индексе отсутствует сезонность.

Проверим остатки модели тренда на соответствие процессу белый шум

1. Отсутствие автокорреляции в остатках.

Для этого приведем график авторегрессионной функции остатков итоговой модели:

Рисунок 9. Авторегрессионная функция остатков модели Брауна

Как видно из рисунка 9 в остатках присутствует авторегрессия первого, второго и более высших порядков, соответственно остатки не соответвуют одному из критериев процесса белый шум, поэтому рассматривать два других критерия не имеет смысла.

Этап 4. Моделирование временного ряда применяя методологию Бокса-Дженкинса.

Анализ динамических рядов часто показывает, что значение показателя в рассматриваемый момент времени находится в некоторой зависимости от значений в предшествующий период. Это явление носит название автокорреляции. Для обнаружения такого эффекта могут быть предложены различные методы.

Предварительный анализ АКФ, ЧАКФ:

Рисунок 10. Автокорреляционная функция индекса РТС.

Рисунок 11. Частная автокорреляционная функция индекса РТС.

Описательная статистика временного ряда говорит о наличии автокорреляции 6-ого порядка. Частная автокорреляционная функция имеет 3 значимых показателя в первом, третьем и двенадцатом лагах.

Проверим временной ряд на стационарность при помощи расширенного теста Дикки-Фуллера. Расширенный критерий Дикки-Фуллера предполагает оценить параметры модели:

при помощи критических значений статистик Дикки-Фуллера,

где – коэффициенты при дополнительных лаговых переменных;

– номер включенного дополнительного лага;

– остатки без автокорреляции, т.е. «белый шум».

В нашем случае, мы проверяем значимость только параметра . Данная проверка носит название теста на наличие единичных корней (unit-root test). Нулевая гипотеза: , т.е. ряду соответствует единичный корень (временной ряд нестационарен). Альтернативная гипотеза: | | < 1 – временной ряд стационарен.

Для проведения теста на наличие единичных корней воспользуемся возможностями пакета Eviews:

Null Hypothesis: RTS has a unit root
Exogenous: Constant
Lag Length: 2 (Automatic - based on AIC, maxlag=11)
				t-Statistic		Prob.*
Augmented Dickey-Fuller test statistic			-2.107959		0.2421
Test critical values:	1% level			-3.503879
	5% level			-2.893589
	10% level			-2.583931
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(RTS)
Method: Least Squares
Date: 11/14/12 Time: 23:55
Sample (adjusted): 2005M04 2012M10
Included observations: 91 after adjustments
Variable	Coefficient	Std. Error		t-Statistic		Prob.
RTS(-1)	-0.054956	0.026071		-2.107959		0.0379
D(RTS(-1))	0.193071	0.102805		1.878034		0.0637
D(RTS(-2))	0.222954	0.103449		2.155199		0.0339
C	22.72194	11.49079		1.977405		0.0512
R-squared	0.130041	Mean dependent var				1.580769
Adjusted R-squared	0.100042	S.D. dependent var				50.42421
S.E. of regression	47.83548	Akaike info criterion				10.61637
Sum squared resid	199076.3	Schwarz criterion				10.72674
Log likelihood	-479.0450	Hannan-Quinn criter.				10.66090
F-statistic	4.334903	Durbin-Watson stat				2.042743
Prob(F-statistic)	0.006765

Таблица №11. Расширенный тест Дикки-Фуллера.

Полученный уровень значимости (Prob. = 0,0068) свидетельствует, что нулевая гипотеза о наличии единичного корня не отвергается, а, следовательно, исходный ряд стационарен относительно стохастического тренда. Также можно рассуждать следующим образом: процесс y_t стационарен, т.к. параметр получился отрицательным и по модулю меньше единицы. Таким образом, временной ряд относится к классу TSP (с детерминированным трендом).

Таким образом, параметр d можно ставить равным 0.

Приведем сравнения моделей ARIMA с разными параметрами, так чтобы уменьшить среднеквадратическую ошибку RMSE:

(A) ARIMA(6,0,3)

(B) ARIMA(1,0,0)

(C) ARIMA(2,0,1) with constant

(D) ARIMA(2,1,0)

(E) ARIMA(2,0,1)

Estimation Period

Model	RMSE	MAE	MAPE	ME	MPE
(A)	53,5838	40,6769	13,3374	1,88338	1,57892
(B)	50,413	36,4728	10,7884	3,76197	0,406907
(C)	46,5466	34,4186	10,3614	0,029689	-0,777941
(D)	48,7763	36,5139	10,6609	1,11432	0,36702
(E)	48,5493	36,0222	10,5782	4,9963	1,75041

Таблица №12. Сравнение ARIMA моделей. Показатели информационной пригодности для обучающей выборки

Model	RMSE	RUNS	RUNM	AUTO	MEAN	VAR
(A)	53,5838	OK	OK	OK	OK	OK
(B)	50,413	OK	OK	OK	OK	OK
(C)	46,5466	OK	OK	OK	OK	OK
(D)	48,7763	OK	OK	OK	OK	OK
(E)	48,5493	OK	OK	OK	OK	*

Таблица №13. Сравнение ARIMA моделей. Тесты основных гипотез.

Validation Period

Model	RMSE	MAE	MAPE	ME	MPE
(A)	8,58048	7,07664	2,65721	1,68867	0,607385
(B)	6,76632	6,71417	2,54123	1,95899	0,715411
(C)	11,4259	8,66445	3,30967	-8,66445	-3,30967
(D)	7,06	5,71745	2,16912	-1,48085	-0,593942
(E)	9,16633	8,92219	3,37171	4,95364	1,84793

Таблица №14. Сравнение ARIMA моделей. Показатели информационной пригодности для тестовой выборки

Модель E можно сразу же отбросить, так как в остатках нарушается условие постоянства дисперсии (VAR), т.е. ее остатки не соответствуют процессу белый шум. Модель A имеет довольно большое значение среднеквадратической ошибки по сравнению со всеми остальными, так же не все параметры модели получились значимыми, поэтому она тоже отбрасывается.

Модель D имеет довольно малую среднеквадратическую ошибку, но его параметры значимы не для всех уровней значимости, поэтому его тоже следует отбросить.

Если смотреть на график автокорреляционной функции остатков модели B, то обнаружится, что в них присутствует автокорреляция первого и второго порядков.

Заметим, что для оставшейся модели RMSE для тестовой выборки самое большое, однако, этот же показатель на всей выборке получился самым маленьким на всей обучающей выборке. Все параметры модели значимы, поэтому выберем для прогноза именно эту модель. Приведем ее параметры и график:

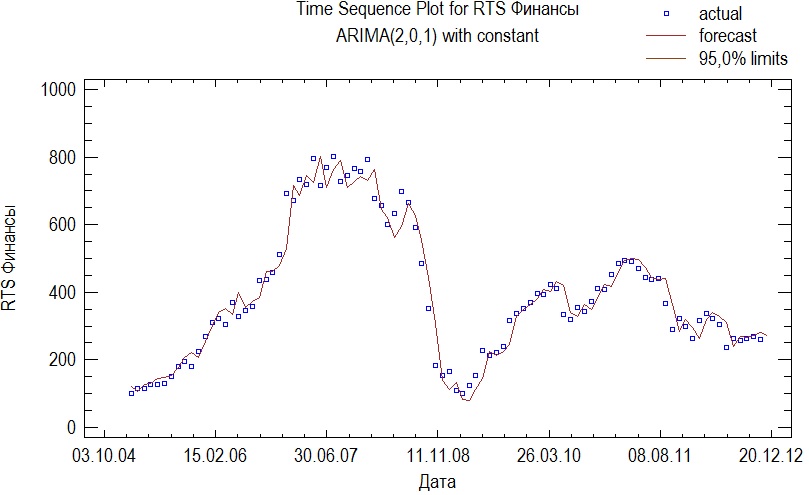
Рисунок №12. График модели ARIMA(2,0,1) с константой.

Parameter	Estimate	Stnd. Error	t	P-value
AR(1)	1,94646	0,0361762	53,8051	0,000000
AR(2)	-0,960507	0,0346632	-27,7097	0,000000
MA(1)	0,916148	0,0651662	14,0586	0,000000
Mean	402,705	36,0374	11,1746	0,000000
Constant	5,65512

Таблица №15. Оценка параметров модели ARIMA(2,0,1).

Приведем таблицу прогноза на 30.11.2012 года.

		Lower 95,0%	Upper 95,0%
Period	Forecast	Limit	Limit
30.11.12	271,84	179,194	364,486

Таблица №16. Интервальный прогноз по модели ARIMA(2,0,1).

Вычисляется по формуле: