Отсутствие автокорреляции в остатках.
Для этого приведем график авторегрессионной функции остатков итоговой модели:
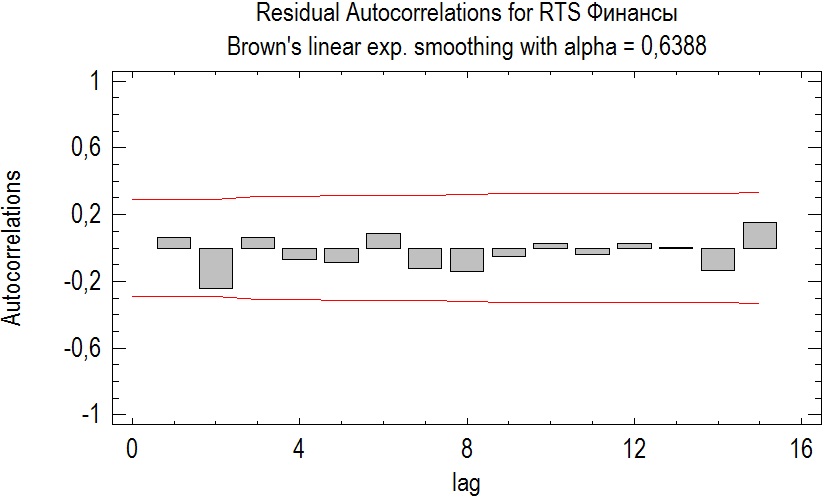
Рисунок 5. Авторегрессионная функция остатков модели Брауна
Как видно из рисунка ни одно из значений авторегрессии не получилось значимым, следовательно, остатки данной модели удовлетворяют первому условию процесса белый шум.
Постоянство дисперсии.
Для этого разобьем исходные данные на две подвыборки объемом 22 и 23 значения. И с помощью Statgraphics проверим гипотезу о равенстве их стандартных отклонений:
F-test to Compare Standard Deviations
Null hypothesis: sigma1 = sigma2
Alt. hypothesis: sigma1 NE sigma2
F = 0,887493 P-value = 0,781894
Do not reject the null hypothesis for alpha = 0,05
Исходя из полученных результатов, можно сказать, что наилучшая модель Брауна удовлетворяет уже двум условиям процесса белый шум. Поэтому проверим последнее.
Равенство нулю математического ожидания остатков.
Данная гипотеза проверяется с помощью t-статистики Стьюдента, где расчетное значение высчитывается по формуле:
Очевидно, что полученное значение гораздо меньше табличного значения распределения Стьюдента, что доказывает гипотезу о равенстве математического ожидания остатков модели нулю.
Таким образом, все условия для процесса белый шум выполнены, данная модель пригодна для прогноза.
Этап 3. Моделирование временного ряда с помощью аналитических методов. Выделение тренда в исходном ряде.
Тренд характеризует основную закономерность изменения во времени значений рассматриваемого показателя, то есть тренд – это детерминированная составляющая динамики развития, которая обуславливается действием постоянных факторов. Уровни временного ряда в этом случае могут быть описаны следующим уравнением:
где
–
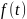систематическая составляющая,
характеризующая основную тенденцию
изменения уровней показателя от времени,
–
случайная составляющая временного
ряда.
На первом этапе лабораторной работы мы выяснили, что исходный временной ряд нестационарен, т.е. существует тенденция во времени. Чтобы выбрать тип трендовой модели запустим в Statgraphics процедуру Forecast ⟶ Automatic Model Selection ⟶ Model Comparison:
Model |
RMSE |
MAE |
MAPE |
ME |
MPE |
(A) Constant mean = 333,053 |
95,9216 |
75,8262 |
29,9311 |
4,52E-14 |
-12,5967 |
(B) Linear trend = 222,728 + 0,0504575 t |
94,9037 |
79,7093 |
30,0041 |
3,36E-14 |
-11,499 |
(C) Quadratic trend = -2695,31 + 2,82297 t + -0,000637792 t^2 |
45,9099 |
39,7373 |
12,867 |
1,41E-13 |
-2,28173 |
(D) Exponential trend = exp(5,20016 + 0,000255026 t) |
98,1333 |
85,1068 |
29,7553 |
14,8119 |
-5,9882 |
(E) S-curve trend = exp(6,54687 + -1667,9 /t) |
95,5024 |
83,671 |
28,3111 |
13,0078 |
-5,14621 |
Таблица 7. Сравнение моделей тренда.
Из таблицы очевидно, что наилучшей моделью является квадратичный тренд, почти все показатели информационной пригодности меньше в два раза, чем для остальных моделей.
Проведем более подробный анализ параметров модели:
Parameter |
Estimate |
Stnd. Error |
t |
P-value |
Constant |
-2695,31 |
256,275 |
-10,5173 |
0,000000 |
Slope |
2,82297 |
0,242775 |
11,6279 |
0,000000 |
Quadratic |
-0,000637792 |
0,0000561451 |
-11,3597 |
0,000000 |
Таблица 8. Оценка параметров модели квадратичного тренда.
Таким образом, уравнение модели будет выглядеть следующим образом:
Построим прогноз и доверительный интервал для периода 01.11.2012 по модели, построенной по значениям, включаемым как обучающую, так и тестовую выборки:
которые, рассчитываются по формуле:
|
|
Lower 95,0% |
Upper 95,0% |
Period |
Forecast |
Limit |
Limit |
30.11.12 |
114,177 |
4,10831 |
224,247 |
Таблица 9. Интервальный прогноз по модели квадратичного тренда
График модели квадратичного тренда выглядит следующим образом:
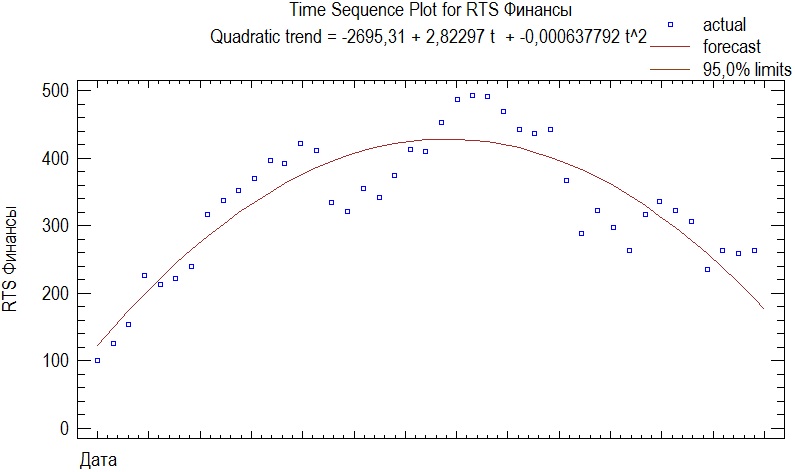
Рисунок 6. Модель квадратичного тренда.