2. Стандартная ошибка модели (rmse):

где v – количество степеней свободы (v = n-m-1).

Однако, из-за возникшего в 2008 году кризиса мы будем рассматривать только те значения, которые идут после достижения наименьшего значения индексом РТС, т.е. с 28.02.2009 по 31.10.2012 (45 месяцев)

Модель	m	RMSE	Кт
A	2	43,0036	0,01461
B	3	49,3698	0,01888
C	4	54,4788	0,02264
D (Mean)	n	95,9216	0,07502

Таблица 3. Сравнение моделей скользящей средней.

При сравнении полученных характеристик, можно сделать вывод, что наилучшим вариантом прогнозирования на основе скользящей средней является модель адаптивной скользящей средней с продолжительностью интервала сглаживания равного двум. Построим для данного варианта прогнозирования доверительный интервал прогноза на 30.11.2012 (95-ый месяц):

		Lower 95,0%	Upper 95,0%
Period	Forecast	Limit	Limit
30.11.2012	264,7	161,472	367,928

Таблица 4. Полученный прогноз по наилучшей модели скользящей средней

который рассчитывается по формуле

1. Отсутствие автокорреляции в остатках.

Для этого приведем график авторегрессионной функции остатков итоговой модели:

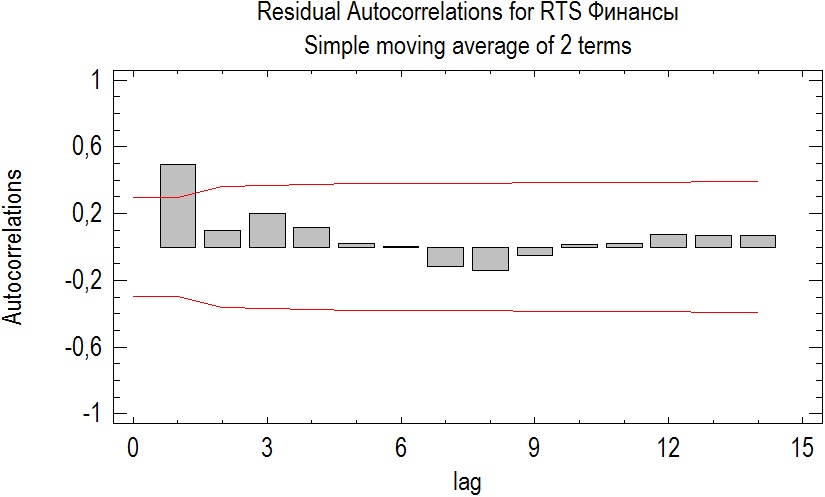
Рисунок 4. Авторегрессионная функция остатков модели скользящей средней

Как видно из рисунка для данной модели присутствует авторегрессия первого порядка, таким образом, нарушается одно из условий для процесса белый шум. Остатки наилучшей модели скользящей средней оказались не соответствующими заданным критериям. Поэтому проверять два оставшихся условия не имеет необходимости.

Метод экспоненциального сглаживания (модель Брауна).

При использование метода экспоненциального сглаживания влияние прошлых наблюдений должно затухать по мере удаления от момента времени, для которого определяется средняя, в отличие от метода скользящей средней, где оно высчитывалось с одинаковыми весовыми коэффициентами. Простая форма модели Брауна записывается следующим образом:

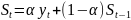
где:

- текущее значение экспоненциальной средней в момент t;

α- коэффициент, характеризующий вес текущего наблюдения при расчёте экспоненциальной средней 0 < α< 1. Еще называют сглаживающим фильтром, через него устанавливается баланс между влиянием на значение текущей модельной оценки уровня ряда и предшествующих модельных оценок.

Также как и в прошлом пункте проведём серию экспериментов, анализируя зависимость точности прогнозирования от (с шагом 0,2) и применим оптимизация для модели с наилучшими показателями.

Для оценки точности прогнозирования используем те же показатели, что и в прошлом пункте, а именно:

1. Коэффициент несоответствия Тейла (K_T).

2. Стандартная ошибка модели (RMSE).

Результаты представим в виде таблицы 5:

	RMSE	КT
0,1	80,0525	0,0528
0,3	48,8842	0,0197
0,5	39,6979	0,0130
0,7	38,8135	0,0124
0,9	42,0973	0,0146

Таблица 5. Сравнение моделей экспоненциального сглаживания Брауна.

При сравнении полученных характеристик, можно сделать вывод, что наилучшим вариантом прогнозирования на основе модели Брауна первого порядка является модель, для которой коэффициент α = 0,7. Применив для нее оптимизацию в Statgraphics получим α = 0,639

Построим для модели с коэффициентом α = 0,639 доверительный интервал прогноза на 30.11.2012 (95-ый месяц):

		Lower 95,0%	Upper 95,0%
Period	Forecast	Limit	Limit
30.11.2012	260,123	184,582	335,664

Таблица 6. Результат прогноза по наилучшей модели Брауна.

который рассчитывается по формуле:

Далее проверим остатки модели на их соответствие процессу белый шум: