Государственное образовательное учреждение

высшего профессионального образования

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»

Институт информационных систем управления

Кафедра математических методов в управлении

Лабораторная работа №1

По дисциплине «МСЭПиЭ»

Выполнил:

студент IV курса

ИИСУ

специальности

«Математические методы

в экономике»

Д.П. Бевз

Проверила: С.А. Аксюк

Москва – 2012

Оглавление

Этап 1. Анализ динамики исходного временного ряда. 3

Проверка ряда на стационарность. 4

Гипотеза о равенстве средних. 4

Гипотеза о равенстве дисперсий. 4

Графический анализ. 5

Проверка ряда на случайность. 6

Расчет критерия серий по медиане выборки. 6

Расчет критерия восходящих и нисходящих серий. 7

Этап 2. Моделирование временного ряда с помощью алгоритмических моделей. 8

Метод адаптивной скользящей средней. 8

Метод экспоненциального сглаживания (модель Брауна). 10

Этап 3. Моделирование временного ряда с помощью аналитических методов. 13

Выделение тренда в исходном ряде. 13

Выявление сезонной составляющей. 14

Этап 4. Моделирование временного ряда применяя методологию Бокса-Дженкинса. 17

Этап 5. Выбор лучшей модели прогноза. 20

Этап 6. Построение прогноза по полученной модели. 21

Приложение. 22

Этап 1. Анализ динамики исходного временного ряда.

Исследуется индекс РТС по отрасли – финансы с января 2005 года по октябрь 2012 года (94 месяца). Представим ряд на графике:

Рисунок 1. Динамика исходного ряда.

Из графика видно, что из-за глобального экономического кризиса, развернувшегося в 2008 году, тенденция динамики индекса РТС существенно изменилась, возможно, при применении декомпозиционного подхода необходимо будет исследовать ряд только с начала 2009 года, когда началось возобновление роста экономики.

Проверка ряда на стационарность. Гипотеза о равенстве средних.

Делим исходные данные на 2 равные части и проверим о гипотезу, о равенстве их средних, воспользовавшись Statgraphics функцией Compare Independent Samples:

	Первая половина	Вторая половина
Count	47	47
Average	323,159	457,233
Standard deviation	101,601	243,995
Coeff. of variation	31,4399%	53,3634%
t test to compare means Null hypothesis: mean1 = mean2 Alt. hypothesis: mean1 NE mean2 assuming equal variances: t = -3,47769 P-value = 0,0007743 Reject the null hypothesis for alpha = 0,05.

Таблица 1. Сравнение средних двух частей выборки

Формула для расчета t-статистики следующая:

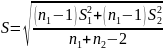
Из результатов, полученных в Statgraphics можно сделать вывод о том, что нулевая гипотеза о равенстве средних двух подвыборок отвергается. Таким образом, можно сделать вывод о нестационарности процесса.

Гипотеза о равенстве дисперсий.

Так же воспользуемся Statgraphics:

	Первая половина	Вторая половина
Standard deviation	101,601	243,995
Variance	10322,8	59533,5
Df	46	46
Ratio of Variances = 0,173394 F-test to Compare Standard Deviations Null hypothesis: sigma1 = sigma2 Alt. hypothesis: sigma1 NE sigma2 F = 0,173394 P-value = 2,30321E-8 Reject the null hypothesis for alpha = 0,05

Таблица 2. Сравнение дисперсий двух частей выборки.

Для сравнения дисперсий применяется критерий Фишера, для этого рассчитывается значение F-статистики по формуле:

На основе, данных полученных при использование Statgraphics можно сделать вывод, что нулевая гипотеза о равенстве средних отвергается, что говорит о присутствии тенденции в ряде.