Предельный закон распределения экстримальных членов вариационного ряда.

N независимых и случайно распределенных случайных величин.

,

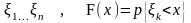
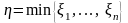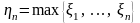
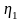- минимальный член вариационного ряда.

- максимальный член вариационного ряда.

Рассмотрим выборку объема n из генеральной совокупности с запасом

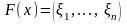
Их расположим в возрастающем порядке: .

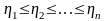Последовательность 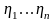- вариационный ряд.

Надо найти закон распределения , это наиболее важная задача.

- зависимые величины.

Надо найти

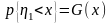
Найдем:

,

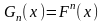
Если зафиксировать x и увеличить n, то если 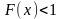, тогда .

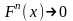Для фиксированного x предельный закон неинтересен. Надо найти последовательность x_1… x_{n …} и 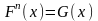- некоторый предельный закон.

1-ый случай: F(x) задает распределение на конечном отрезке .

,

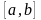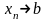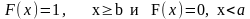
Рассмотрим , .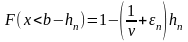

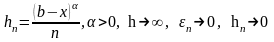Тогда можно рассчитывать на сходимость.

Тогда:

.

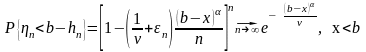Закон третьего типа:

;

.

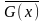
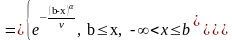
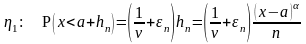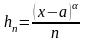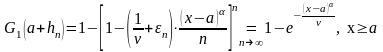
Предельный закон третьего типа.

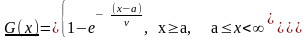
Пример:

Равномерное распределение в .

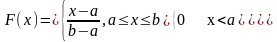
Положим 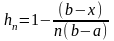, тогда

,

;

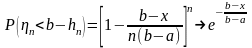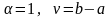
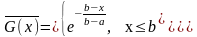
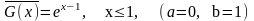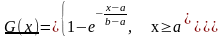
Законы 1 – ого типа (двойной показательный закон)

, поэтому надо брать , .

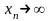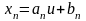Можно доказать, что, если 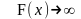с показательной скоростью, то можно подобрать такие 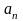и 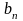, чтобы был выполнен предельный закон:

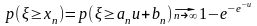, если .

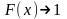Пример 1:

.

;

.

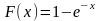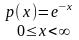
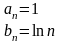
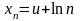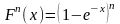
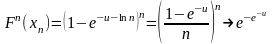Пример 2:

F- распределение.

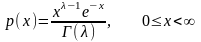
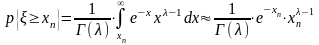(хорошее приближение).

По правилу Лопиталя: .

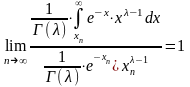Поэтому: .

Предлагается взять 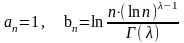, то есть:

.

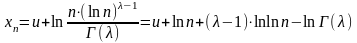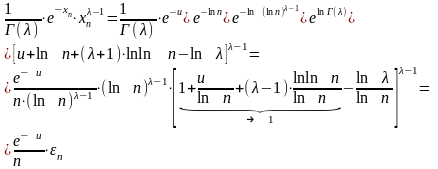
то есть:

;



.

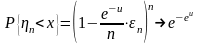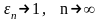
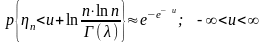
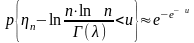Пример 3: Нормальный закон.

;

.

.

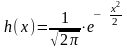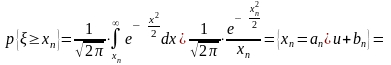
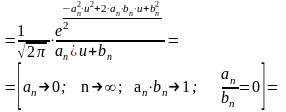
Отсюда видно, что .

.

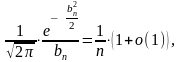
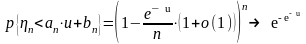Формула Хинчина – Леви. Определение

Случайная величина   называется бесконечно делимой, если для любого   она может быть представлена в виде

,

где   - независимые, одинаково распределённые случайные величины.

Свойства бесконечно делимых распределений[

• Характеристическая функция   бесконечно делимой случайной величины   имеет вид:

.

• Характеристическая функция бесконечно делимого распределения не обращается в нуль.

• Функция распределения суммы независимых случайных величин, имеющих бесконечно делимые функции распределения, также бесконечно делима.

• Функция распределения, предельная для последовательности бесконечно делимых функций распределения, является бесконечно дел

Формула Леви — Хинчина[

Пусть   - характеристическая функция бесконечно делимого распределения на  . Тогда существует неубывающая функция ограниченной вариации  , такая что

Пример.

• Следующие распределения бесконечно делимы: распределение Коши, распределение Пуассона, нормальное распределение, гамма распределение.

• Пусть задано вероятностное пространство  , где

для некоторого  . Тогда случайная величина  , имеющая вид

не является бесконечно делимой.

Теорема Шварцшильда. Шварцшильдовские координаты

В так называемых Шварцшильдовских координатах  , из которых 3 последних аналогичны сферическим, метрический тензор наиболее физически важной части пространства-времени Шварцшильда с топологией   (произведение области двумерного евклидова пространства и двумерной сферы) имеет вид

Интервал в этой метрике записывается как

где   — так называемый радиус Шварцшильда, или гравитационный радиус,   — масса, создающая гравитационное поле (в частности, масса чёрной дыры),  — гравитационная постоянная,   — скорость света.

Координата   не является длиной радиус-вектора, а вводится так, чтобы площадь сферы   в данной метрике была равна  . При этом «расстояние» между двумя событиями с разными   (но одинаковыми остальными координатами) даётся интегралом

При   или   метрика Шварцшильда стремится (покомпонентно) к метрике Минковского в сферических координатах, так что вдали от массивного тела  пространство-время оказывается приблизительно псевдоевклидовым сигнатуры  . Так как   при   и   монотонно возрастает с ростом  , то собственное время в точках вблизи тела «течёт медленнее», чем вдалеке от него, то есть происходит своеобразное гравитационное замедление времени массивными телами.