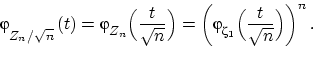§ 4. Доказательство центральной предельной теоремы

Пусть   — последовательность независимых в совокупности и одинаково распределённых случайных величин с конечной и ненулевой дисперсией. Обозначим через   математическое ожидание   и через   — дисперсию  . Требуется доказать, что

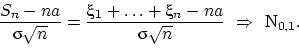
Доказательство. Введём стандартизованные случайные величины   — независимые случайные величины с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть   есть их сумма  . Требуется доказать, что  .

Характеристическая функция величины   равна

(27)

Характеристическую функцию случайной величины   можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты  ,  . Получим

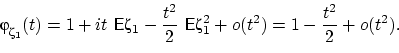
Подставим это разложение, взятое в точке  , в равенство (27) и устремим   к бесконечности. Ещё раз воспользуемся замечательным пределом.

В пределе получили характеристическую функцию стандартного нормального распределения. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости

Теорема Бернштейна (центральная придельная теорема):

Если 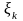- независимы, 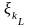- усеченные величины

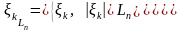
то к применима центральная предельная теорема с параметрами

, ,

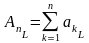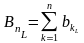если выполнены условия:

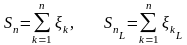
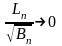(Б.1)

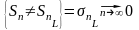(Б.2)

Если выполняется (Б.1) и (Б.2), то

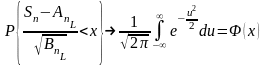(3)

Доказательство:

По лемме к применима центральная предельная теорема

с этими параметрами.

+ = ,

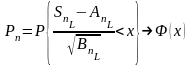
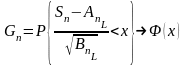
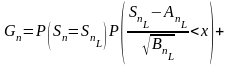
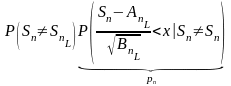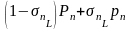где

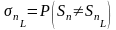
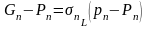
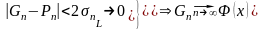
ч.т.д.

Замечание к теореме Бернштейна:

Предположим, что 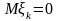, 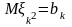и ,

,

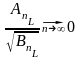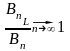тогда, если выполняется (Б.1) и (Б.2), то верна центральная предельная теорема:

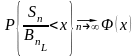
Доказательство:

Из (1) и (2) 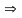(3)

=

=

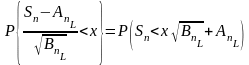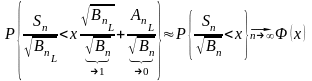
ч.т.д.

Теорема

Если выполняется условие Линденберга, то выполняется условие теоремы Бернштейна и выполняется условие в замечании

,

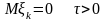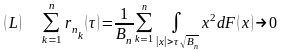
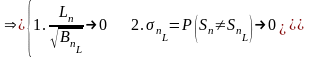
Доказательство:

Зададим 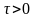, возьмем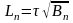

, =

=

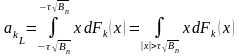
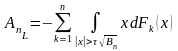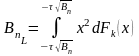
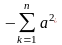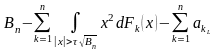
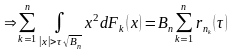
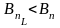
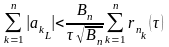
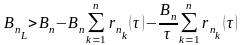
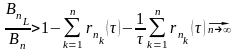1

Оценка снизу совпадает с оценкой сверху

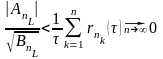
1.

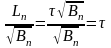
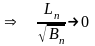
2. <

=

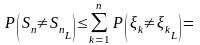
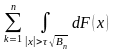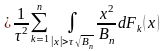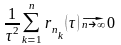
ч.т.д.

Доказательство теоремы Ляпунова(в общем случае):

-независимые случайные величины, ,

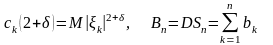
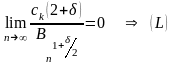
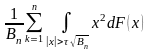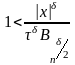Рассмотрим . Т.к. , то

< =

=

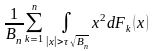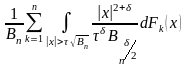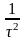
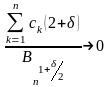
ч.т.д.

Пример Бернштейна:

Пусть , (k=1,..,n)-независимые и одинаково распределенные случайные величины.

=

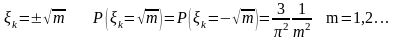
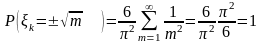
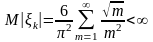
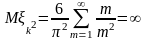
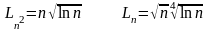
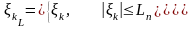
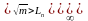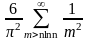
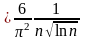
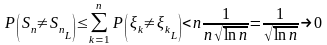
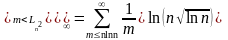
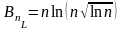
Пример 2:

Если k не является полным квадратом, то с вероятностями

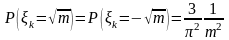
Если k -полный квадрат, то с вероятностями

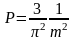
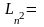
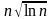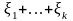. К применима центральная предельная теорема.

БЕЗГРАНИЧНО ЦЕЛЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Определение:

Закон распределения 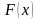случайной величины называется безгранично целым, если может быть представлен как сумма n независимых, одинаково распределенных величин.

= ,

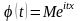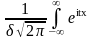
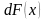тогда 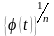- есть характеристическая функция.

Пример:

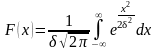
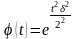
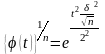
Нормальный закон – безгранично делим.

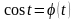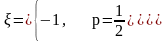
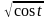характеристическая функция

- не характеристическая функция.

Лемма 1

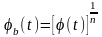
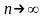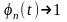, , , -T < t < T

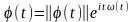
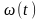- главный аргумент,

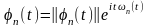
Надо доказать, что , .

,

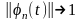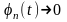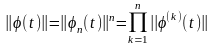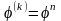
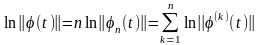
Необходимые условия сходимости:

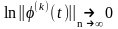, необходимые условия есть

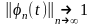
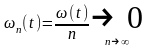
Лемма 2

Характеристическая функция безгранично делимого закона нигде не обращается в 0.

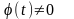-T < t < T

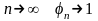
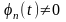-T < t < T т. е.

Примеры:

Характеристические функции бесконечно делимых законов:

• Нормальный закон

• Закон Коши

• Закон Пуассона

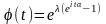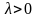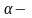, , вещественное,

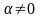
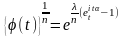
- характеристическая функция закона Пуассона.