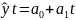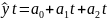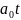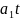3.1. Прогнозування збуту продукції фг «Едельвейс – 2»
На сучасному етапі розвитку економіки України особливу увагу привертає проблема запровадження елементів планування та прогнозування на підприємстві, гарантування їх економічної безпеки та оцінка їх ефективності за допомогою математичного апарату. Тобто йдеться про використання економіко-математичних методів та моделей для розв’язання задач планування і прогнозування. Структурні зміни, що мають місце у ринковій економіці України позитивно вплинули на розвиток частини підприємств, які порівняно з іншими, змогли швидко досягти достатньо високих обсягів виробництва продукції. Однак деяким із них притаманний ряд невирішених проблем. Загальним завданням для господарських суб’єктів є зміцнення позицій на внутрішньому ринку, підтримка ділових стосунків з іноземними партнерами та ін. Вирішення цих завдань потребує запровадження на підприємствах прогресивних методів прогнозування та планування.
Прогноз кон'юнктуру ринку повинен спрямовуватись, перш за все, на визначення основних тенденцій науково-технічного прогресу в галузі, в якій діє господарство.
Отже, прогнозування збуту продукції - це визначення того, що підприємство розраховує продати, виходячи з існуючої кон'юнктури, ринкового потенціалу і власних можливостей.
Прогнозування збуту продукції ФГ «Едельвейс – 2» залежить від дії двох груп чинників:
- контрольованих: ціни, канали розподілу, система просування, характеристики продукції, товарна політика підприємства;
- неконтрольованих: стан економіки, темпи інфляції, процентні ставки, демографічні зміни, смаки споживачів, конкуренція, стан галузі.
Звідси прогнозування збуту повинно враховувати можливості господарства стосовно управління контрольованими чинниками і прилаштовування під дію неконтрольованих змінних.
На основі інформації, що надало мені господарство, я пропоную спрогнозувати загальний обсяг продажу продукції ФГ «Едельвейс – 2» на 2014 і 2015 рік, а в розрізі окремих видів продукції на 2012 рік.
Таблиця 3.1.
Ретроспективні дані по обсягам продажу ФГ «Едельвейс – 2» в розрізі видів продукції, тис. грн.
Вид Продукції |
Роки |
||||||||
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Помідори |
|
|
|
517,4 |
473,9 |
1344,4 |
3224,4 |
2015,3 |
1130,8 |
Огірки |
|
|
160,7 |
247,3 |
254,1 |
282,2 |
348,5 |
330,2 |
324,7 |
Цибуля |
1937,2 |
1987,3 |
2078,9 |
2145,8 |
2355,6 |
3166,1 |
3421,7 |
4562,9 |
5132,7 |
Капуста |
|
|
|
196,3 |
257,1 |
208,6 |
954,4 |
2934,2 |
3568,4 |
Морква |
1035,4 |
1327,6 |
1575,1 |
1691,6 |
1999,9 |
1510,3 |
2455,9 |
1598,9 |
988,5 |
Буряки столові |
|
|
|
|
|
|
210,2 |
569,4 |
678,1 |
Ягоди (суниця) |
|
|
|
|
|
|
|
15,8 |
22 |
Баштанні |
|
|
|
|
|
|
|
|
2175,7 |
Разом |
2972,6 |
3314,9 |
3814,7 |
4798,4 |
5340,6 |
6511,5 |
10615,1 |
12026,7 |
14020,9 |
Джерело: Розрахунки автора за даними звітів підприємства
З таблиці 3.1. чітко видно, що господарство вирощувало і скільки реалізовувало продукції на протязі свого існування. «Старожилами» можна вважати тільки такі види продукції, як цибуля і морква. Для прогнозування обсягів продажу ФГ «Едельвейс – 2» на 2012 рік в розрізі кожного виду продукції я здійснюватиму за допомогою методу екстраполяції, а саме методу зі знаходженням коефіцієнта середньорічного темпу росту.
Розрахунок даного методу здійснюється за наступною формулою:
;
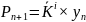Середньорічний темп зростання розраховується за формулою:
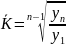
де,
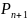– прогнозоване значення економічного
показника;
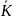– середньорічний
темп зростання;
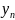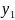– кінцевий
показник динамічного ряду;
-
початковий показник динамічного ряду;
n – кількість показників в динамічному ряду;
і – період на який прогнозується.
Прогнозування обсягу продажу на 2012 рік не буде здійснюватися для суниці і баштанних, адже ці види продукції вирощувалися і реалізовувались менше трьох років.
Розрахунок прогнозу обсягів продажу буде здійснюватися на основі даних, що зазначенні в таблиці 3.1.1.
Почнемо прогноз, з прогнозування обсягу продажу помідорів на 2012 рік:
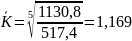
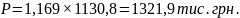
Обсяг продажу збільшився на 191,1 тис. грн.
Прогнозування обсягу продажу огірків:
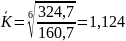
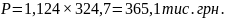
Обсяг продажу збільшився на 40,4 тис. грн.
Прогнозування обсягу продажу цибулі:
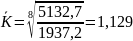
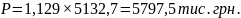
Обсяг продажу збільшився на 664,8 тис. грн.
Прогнозування обсягу продажу капусти:
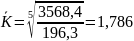
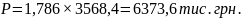
Обсяг продажу збільшився на 2805,2 тис. грн.
Прогнозування обсягу продажу моркви:
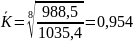
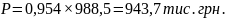
Обсяг продажу зменшився на 44,8 тис. грн.
Прогнозування обсягу продажу буряків (столових):
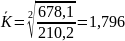
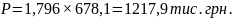
Обсяг продажу збільшився на 539,8 тис. грн.
Прогнозування загального обсягу продажу овочевої продукції ФГ «Едельвейс – 2» на 2012 рік:
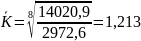
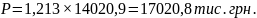
В загальному обсяг продажу по господарству на 2012 р збільшився на 3 млн. грн., що є досить позитивним результатом.
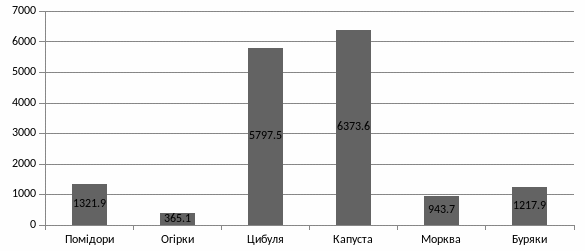
Рис. 3.1. Прогнозовані обсяги реалізованої продукції ФГ «Едельвейс – 2» на 2012 р, тис. грн..
Джерело: Розрахунки автора за даними звітів
Таблиця 3.1.2.
Для здійснення прогнозу за допомогою методу математичного моделювання потрібні векторні коефіцієнти для лінійних функцій і значення узагальнюючого коефіцієнта лінійних функцій (табл. 3.1.3).
Таблиця 3.2.
Векторні коефіцієнти для лінійних і квадратичних функцій
Довжина ряду |
|
|
||||
|
|
|
|
|
||
1 |
66 |
-9 |
1188 |
-402 |
30 |
|
2 |
55 |
-7 |
660 |
-166 |
10 |
|
3 |
44 |
-5 |
242 |
15 |
-5 |
|
4 |
33 |
-3 |
-66 |
141 |
-15 |
|
5 |
22 |
-1 |
-264 |
212 |
-20 |
|
6 |
11 |
1 |
-352 |
228 |
-20 |
|
7 |
0 |
3 |
-330 |
189 |
-15 |
|
8 |
-11 |
5 |
-198 |
85 |
-5 |
|
9 |
-22 |
7 |
44 |
-54 |
10 |
|
10 |
-33 |
9 |
396 |
-258 |
30 |
|
μ |
165 |
1320 |
||||
Так як динамічний ряд стабільний і не має коливань, прогноз буде здійснюватися за допомогою методу лінійних функцій.
Метод лінійних функцій має наступну формулу для розрахунку:
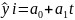
де,
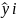- прогнозоване значення економічного
показника;
,
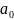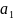- параметри рівняння лінійної функції;
t – номер прогнозованого періоду
Розрахунок параметрів рівняння здійснюється за наступними формулами:
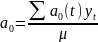
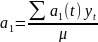
де,
,
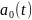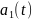– векторні
коефіцієнти
лінійних
функцій;
µ - узагальнюючий коефіцієнт лінійних функцій;
- об’єм продажу.
Таблиця 3.3.
Дані для розроблення моделі лінійної функції прогнозування обсягів продажів ФГ «Едельвейс – 2»
Роки |
№ періоду, t |
Продаж, тис грн. |
|
|
|
|
2003 |
1 |
2972,6 |
66 |
-9 |
196191,6 |
-26753,4 |
2004 |
2 |
3314,9 |
55 |
-7 |
182319,5 |
-23204,3 |
2005 |
3 |
3814,7 |
44 |
-5 |
167846,8 |
-19073,5 |
2006 |
4 |
4798,4 |
33 |
-3 |
158347,2 |
-14395,2 |
2007 |
5 |
5340,6 |
22 |
-1 |
117493,2 |
-5340,6 |
2008 |
6 |
6511,5 |
11 |
1 |
71626,5 |
6511,5 |
2009 |
7 |
10615,1 |
0 |
3 |
0 |
31845,3 |
2010 |
8 |
12026,7 |
-11 |
5 |
-132294 |
60133,5 |
2011 |
9 |
14020,9 |
-22 |
7 |
-308460 |
98146,3 |
2012 |
10 |
17020,8 |
-33 |
9 |
-561686 |
153187,2 |
∑ |
- |
- |
- |
- |
-108615 |
261056,8 |
Джерело: Розрахунки автора за даними звітів
Далі розраховуємо параметри рівняння лінійної функції:
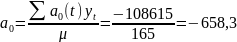
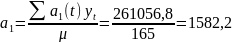
Таким чином модель приймає наступний вигляд:
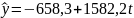
Мною була поставлена задача розрахувати прогноз обсягу продажу овочевої продукції ФГ «Едельвейс – 2» на 2014 і 2015 роки.
Порядкові номери 2014 року буде становити 12, а порядковий номер 2015 року становитиме 13.
Отже, на основі цих даних прогнозуємо, що в 2014 році обсяг продажів овочевої продукції господарства становитиме:
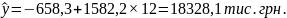
За аналогічним розрахунком здійснюємо прогноз обсягу продажу на 2015 рік:
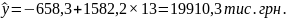
Після здійснення прогнозу необхідно перевірити достовірність прогнозування.
Перевірка достовірності моделі здійснюється за допомогою відносного відхилення розрахункових даних від фактичних. Розрахунок відхилення проводиться за наступною формулою:
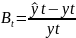
де, Bt – відхилення;
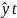– розрахункове
значення показника;
yt – фактичне значення показника.
Модель є достовірною, якщо відносне відхилення на перевищує ± 10%.
Модель є абсолютно точною, якщо відносне відхилення не перевищує ± 5%.
Перевірка достовірності моделі:
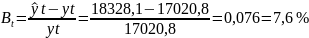
Отже, з проведеного прогнозу можна зробити наступний висновок. Дана лінійна модель являється достовірною, адже значення відносного відхилення на перевищують ± 10%. Але абсолютно точною її не можна вважати, тому що відносне відхилення перевищує 5%.