20.8. Реализация лестничных реактивных четырехполюсников, нагруженных резисторами с одной из сторон

Большое применение на практике находят лестничные реак­тивные четырехполюсники, нагруженные резисторами с одной из сторон. Питание таких четырехполюсников осуществляется от источников тока либо от источников э. д. с. При синтезе таких че­тырехполюсников их передаточные функции выражают через па­раметры холостого хода (Z₁₁, Z₁₂, Z₂₁ и Z₂₂) или короткого замы­кания (Y₁₁, Y₁₂, Y₂₁ и Y₂₁) и активные сопротивления, подключен­ные к их зажимам.

Ограничимся рассмотрением реактивных четырехполюсников при их питании от источника э.д. с. (рис. 20.18 и 20.19). Как пока­зано в разд. 10, передаточную функцию по напряжению для схемы, приведенной на рис. 20.18, можно записать в виде

а для схемы, приведенной на рис. 20.19,— в виде

Если в рассматриваемых четырехполюсниках сопротивление нагрузки r_H или внутреннее сопротивление источника э.д. с. r_i

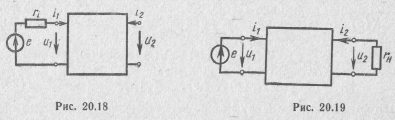
принять равным единице, т. е. осуществить нормирование сопро­тивлений, то выражения для передаточных функций (20.36) и (20.37) примут вид:

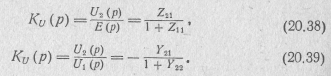
Аналогичную структуру имеют и передаточные функции четы­рехполюсника при подключении к его входным зажимам источника тока [9].

Вначале рассмотрим свойства передаточных функций лестнич­ных четырехполюсников, которые используются при их синтезе.

20.8.1. Свойства передаточных функций лестничных четырехполюсников

Ограничимся рассмотрением свойств передаточного сопротив­ления Z₂₁(p) лестничного четырехполюсника (рис. 20.20). Основ­ным свойством этого сопротивления является то, что его нули со­впадают с полюсами сопротивлений последовательных ветвей и нулями сопротивлений параллельных ветвей. Это можно пояс­нить непосредственно по схеме четырехполюсника (рис. 20.20) исходя из физических соображений или показать математически, Например, для четырехполюсника, состоящего из одной парал­лельной ветви с сопротивлением Z₀ (рис. 20.21), передаточное со­противление

Значит, в этом четырехполюснике нуль Z₂₁(p) совпадает с нулем z₀, т. е. с нулем сопротивления параллельной ветви.

Для четырехполюсника, состоящего из трех ветвей (рис. 20.22), получим

Из этого выражения видно, что нули Z₂₁(p) совпадают с ну­лями сопротивлений параллельных ветвей Z₀ и Z₂ и полюсом со­противления последовательной ветви Z₁.

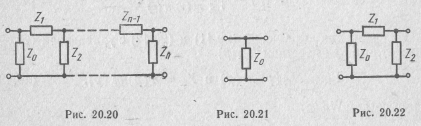
Продолжая этот процесс и дальше, можно убедиться в спра­ведливости указанного выше свойства Z₂₁(p). Однако следует иметь в виду, что для некоторых лестничных четырехполюсников это свойство несправедливо [47].

Поскольку сопротивления ветвей лестничной схемы представ­ляют собой положительные вещественные функции и не имеют ни нулей, ни полюсов в правой полуплоскости, то и нули передаточ­ного сопротивления Z₂₁(p) лестничного четырехполюсника не мо­гут находиться в правой полуплоскости. У реактивных лестничных четырехполюсников нули Z₂₁(p) находятся только на оси jω, а у лестничных четырехполюсников типа rС — только на веще­ственной отрицательной полуоси,