20.6. Понятие о реализации двухполюсников общего типа

В подразд. 18.7 было показано, что необходимым условием, которому должны удовлетворять входные операторные функции Z(p) и Υ(p) линейных пассивных электрических цепей с сосредоточенными параметрами, является то, чтобы эти функции были положительными вещественными функциями. Доказа­тельство достаточности этого условия впервые сделал О. Бруне в 1931 г., пред­ложивший метод реализации пассивных двухполюсников общего типа. Сущность этого метода сводится к разложению заданной положительной вещественной функции в цепную дробь, элементами которой являются простейшие положи­тельные вещественные функции, реализуемые в виде двухполюсников.

Если заданная положительная вещественная функция Z(p) имеет простые полюсы и нули на мнимой оси, то, выделив полюсы этой функции, находя­щиеся на мнимой оси, ее можно представить в виде суммы реактансной функ­ции Z_1p(р) и положительной вещественной функции Z₁₀(p) более низкого по­рядка:

Функция Z₁₀(p) уже не будет иметь полюсов на мнимой оси, но может иметь на этой оси нули. Тогда функция Y₁₀(p)=l/Z₁₀(p) будет иметь полюсы на мнимой оси, и ее можно также представить в виде суммы реактансной функ­ции Y_2p(p) и положительной вещественной функции Y₂₀(p). Тогда

Аналогичный процесс можно продолжать до тех пор, пока оставшаяся функция уже не будет содержать ни полюсов, ни нулей на мнимой оси. Оче­видно, степени полиномов числителя и знаменателя этой оставшейся функции будут одинаковыми, иначе эта функция имела бы или нуль, или полюс при р= , которые можно было бы из нее выделить. Если при p=jω вещественная часть оставшейся функции ни при одном значении ω не равна нулю, то можно вы­делить вещественную положительную постоянную, равную наименьшему значе­нию, вещественной части на мнимой оси, которая реализуется как последова­тельное или параллельное сопротивление в зависимости от того, выражает оставшаяся функция сопротивление или проводимость. После этого описанный выше процесс выделения реактансных функций и вещественных положительных постоянных продолжается до тех пор, пока он либо успешно закончится, либо приведет к положительной вещественной функции, которая после выделения предельно возможной постоянной не имеет на мнимой оси ни нулей, ни полюсов.

В первом из этих случаев заданная положительная вещественная функция может быть представлена в виде лестничного двухполюсника [47].

Если на одном из этапов разложения заданной положительной веществен­ной функции в цепную дробь продолжение процесса оказывается невозможным из-за отсутствия у оставшейся функции нулей и полюсов на мнимой оси, то в этом случае используется предложенный О. Вруне метод, основанный на ис­кусственном введении полюсов в разлагаемую функцию [47].

20.7. Реализация четырехполюсников в виде мостовых схем

Как показано в подразд. 18.4, необходимым условием, которому должны удовлетворять передаточные функции линейных электри­ческих цепей с сосредоточенными параметрами

я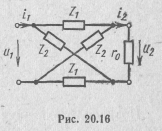 вляется вещественность коэффициентов полиномов числителя и знаменателя, а полином знаменателя V(ρ), кроме того, должен быть полиномом Гурвица.

Чтобы доказать, что эти условия яв­ляются и достаточными, необходимо по­строить хотя бы одну физически осуще­ствимую электрическую цепь с переда­точной функцией, удовлетворяющей ука­занным выше условиям. В качестве такой цепи выберем согласованно нагруженный симметричный мостовой четырехполюс­ник с характеристическим сопротивле­нием Z_C, не зависящим от частоты, т. е. Z_C = r₀ (рис. 20.16). Сопротивления ветвей Z₁ и Z₂ такого четырех­полюсника связаны соотношением

Непосредственным расчетом передаточных функций рассмат­риваемого четырехполюсника по току и по напряжению можно показать, что эти функции одинаковы и равны

Из этого соотношения получим

Так как коэффициенты полиномов K(р) являются веществен­ными, то из выражения (20.33) следует, что Z₁(p) и Z₂(p) яв­ляются вещественными при вещественных значениях р. Кроме того, если |К(р)| 1 при σ 0, то вещественные части Z₁(p) и Z₂(p) будут положительными.

Этих двух условий, как показано в подразд. 18.7, достаточно, чтобы Z₁(p) и Z₂(p) были положительными вещественными функ­циями, которые, как показано в подразд. 20.6, можно реализовать в виде пассивных двухполюсников.

Из этого следует, что указанные в начале подраздела условия, которым должны удовлетворять передаточные функции электриче­ских цепей с сосредоточенными параметрами, являются не только

необходимыми, но и достаточными. Дополнительное условие физи­ческой реализуемости передаточных функций электрических цепей

|K(P)| 1 при σ 0 (20.34)

м ожно выполнить путем умножения заданной передаточной функ­ции, не удовлетворяющей этому условию, на постоянный веще­ственный множитель k<1. Это приводит лишь к частотно-незави­симому уменьшению модуля переда­точной функции |К(р)|, которое мо­жет быть скомпенсировано добавле­нием к цепи каскада с частотно-независимым коэффициентом уси­ления.

Следует отметить, что условие (20.34) можно выполнить только в случае, если степень полинома числителя передаточной функции (20.30) не превосходит степень по­линома ее знаменателя. Порядок реализации заданной передаточной функции в виде согласованно нагруженного симметричного мостового четырехпо­люсника с частотно-независимым характеристическим сопротивле­нием рассмотрим на конкретном примере.

Пример 20.5.

Произвести синтез четырехполюсника по заданной передаточной функции

если его нагрузкой является активное сопротивление r₀, равное 10 кОм.

Решение.

По заданной передаточной функции и сопротивлению нагрузки, используя выражения (20.33), находим Z_t(p) и Z₂(p):

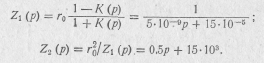
Сопротивление Z₁(p) реализуется в виде параллельного соединения ем­кости С₁ = 5000 пФ и активного сопротивления r=6666 Ом, а сопротивление Z₂(p)—в виде последовательного соединения индуктивности L = 0,5 Г и актив­ного сопротивления r₂=15 кОм (рис. 20.17).

Следует отметить, что поскольку на расположение нулей пере­даточной функции при мостовой реализации не накладывалось никаких ограничений, то этот вид реализации может быть исполь­зован в задачах синтеза как минимально-фазовых, так и немини­мально-фазовых цепей.

Недостатками мостовой реализации являются уравновешенная структура и неоправданно большое число элементов, необходимое для реализации заданной передаточной функции, а также слож-

мая структура плеч в случае передаточных функций высокого по­рядка. Для уменьшения числа элементов иногда применяют четы­рехполюсники с трансформаторами, в которых число элементов уменьшается вдвое.

Для упрощения структуры плеч мостового четырехполюсника иногда применяют каскадное соединение мостовых четырехполюс­ников постоянного характеристического сопротивления с более простой структурой плеч. Для этого заданную передаточную функ­цию К(р) представляют в виде произведения рациональных функций с вещественными коэффициентами:

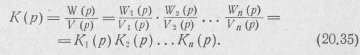
Это представление К(р) можно всегда осуществить таким обра­зом, чтобы каждая из функций K_k(p) удовлетворяла условиям фи­зической реализуемости передаточных функций [47].

Реализовав составляющие K_k(р) в виде мостовых четырехпо­люсников постоянного характеристического сопротивления и со­единив их каскадно, получим сложный четырехполюсник с задан­ной передаточной функцией K(р). При этом общее число элемен­тов цепи остается таким же, как и при реализации той же переда­точной функции K(р) одним четырехполюсником. Однако при этом влияние отклонений параметров элементов от номинальных значений на характеристики цепи уменьшается.

Если по условиям задачи требуется, чтобы синтезируемый че­тырехполюсник был неуравновешенным, то можно от полученного мостового четырехполюсника перейти к эквивалентному неурав­новешенному четырехполюснику или же сразу произвести синтез четырехполюсника с неуравновешенной структурой [47].