20.5. Реализация двухполюсников типа rС

При синтезе двухполюсников типа rС воспользуемся результа­тами, полученными при рассмотрении синтеза двухполюсников типа LC. Для этого установим связь между операторными вход­ными функциями этих двухполюсников.

В выражениях для операторного входного сопротивления Z(p)=Δ_z/Δ₁₁ и операторной входной проводимости Υ(p)= 1/Z(p) = Δ₁₁/Δ_Z цепи rC элементами определителя контурны

уравнений Δ_Z и его алгебраических дополнений Δ₁₁ является опе­раторное сопротивление

Произведя в этом выражении замену p=s², получим

где

Так как множитель 1/s входит во все элементы Δ и Δ₁₁, то для цепи, состоящей из п контуров, получим

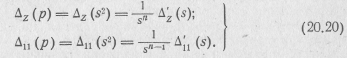
Элементами Δ' (s) и является сопротивление Z_kj(s) (20.19), которое можно рассматривать как сопротивление цепи LC, считая, что r_kj = L_kj и s=p. При этом для входных операторных сопротивлений двухполюсника типа rС получим

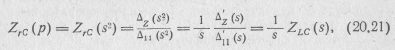
где z_lc(s) — входное операторное сопротивление двухполюсника

типа LC.

Из этого выражения видно, что если входное операторное со­противление двухполюсника типа LC, взятое как функция s, раз­делить на оператор s и заменить s² на р, то получим входное опе­раторное сопротивление двухполюсника типа rC. Так, например, произведя указанные операции с входным операторным сопротив­лением двухполюсника типа LC, определяемым выражением (20.8),

получим

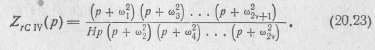
Аналогичным образом из входных операторных сопротивлений двухполюсника типа LC, определяемых выражениями (20.5) —

(20.7), можно получить еще три вида входных операторных сопро­тивлений двухполюсника типа rС:

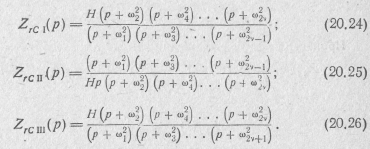
Учитывая чередуемость ω_k, из выражений (20.23) — (20.26) можно установить следующие особенности входных операторных сопротивлений двухполюсников типа rС:

а) высшая степень полинома числителя на единицу меньше или равна степени полинома знаменателя;

б) все полюсы и нули расположены на вещественной отрица­тельной полуоси, являются простыми и взаимно чередуются, при­чем ближайшим к началу координат является полюс (он может, в частности, находиться и в начале координат); полюса в беско­нечности быть не может.

Из выражений, обратных уравнениям (20.23) — (20.26), можно установить следующие особенности входных операторных проводи-мостей двухполюсников типа rС:

а) высшая степень полинома числителя на единицу больше или равна степени полинома знаменателя;

б) все полюсы и нули расположены на вещественной отрица­тельной полуоси, являются простыми и взаимно чередуются, при­чем ближайшим к началу координат является нуль.

Установленная выше связь между входными операторными функциями двухполюсников типа rС и LC позволяет при синтезе двухполюсников типа rС использовать рассмотренные ранее ме­тоды синтеза двухполюсников типа LC.

Для разложения функции Z_rC(p) (20.23) на простые дроби воспользуемся выражением (20.9), которое запишем в виде

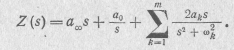
Умножив это выражение на 1/S и заменив s² на р_, на σ_k и 2a_k на a_k, получим

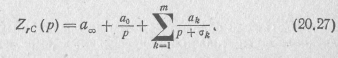
Коэффициенты этого выражения , a₀ и a_k, являющиеся ве­щественными положительными числами, можно определить по формулам:

Первое слагаемое выражения (20.27), соответствующее значе­нию функции Z_rC(p) при p= , можно реализовать в виде актив­ного сопротивления , второе слагаемое, соответствующее

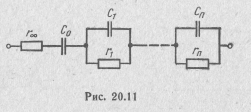
полюсу функции при p=0,— в виде емкости C₀=1/a₀, а каждое из слагаемых a_k/(p+σ_k), соответствующих полюсам функции при р=-σ_k,— в виде цепи, состоящей из параллельного соединения элементов r_k и C_k. Для определения величин r_k и C_k представим a_k/(p+ σ_k) в виде

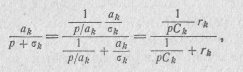
откуда следует, что C_k=l/a_k и r_k=a_k/σ_k.

Схема двухполюсника, соответствующего выражению (20.27), приведена на рис. 20.11.

Для получения разложения функции Y_rC(р) на простые дроби вначале учтем, что в соответствии с формулой (20.21) эту функ­цию можно представить в виде

Y_rC(p) = sY_LC(s). (20.28)

В соответствии с уравнением (20.12) это выражение предста­вим в виде

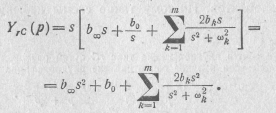
Заменив в этом выражении s² на p, на а_k и 2b_k на b_k, по­лучим

Коэффициенты этого выражения , b₀ и b_k можно определить по формулам:

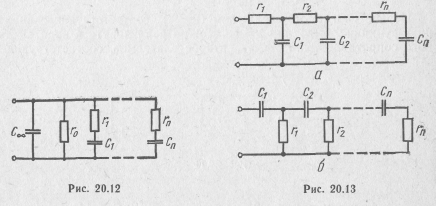
Выражению (20.29) соответствует схема двухполюсника, при­веденная на рис. 20.12, где ; r₀= l/b₀; C_k=b_k/σ_k; r_k = 1/b_k.

Значения величин C_k и r_k получаются из представления b_kp/(р+ σ_k) в виде

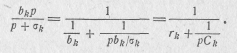
По аналогии с двухполюсниками типа LC можно получить еще два вида схем двухполюсников типа rС (рис. 20.13) путем разло­жения заданной функции сопротивления Z_rC(p) или проводимо­сти Y_rC(p) в непрерывную дробь, начиная деление с высших или низших степеней р.

Следует отметить, что все четыре рассмотренные схемы двух­полюсников типа rС содержат одинаковое, минимально возмож­ное число элементов. Поэтому такие схемы называют каноническими.

Пример 20.4.

Произвести синтез двухполюсника типа rC путем разложения Z_rc(p) в не­прерывную дробь, если входное сопротивление двухполюсника имеет вид

Решение.

Начнем деление числителя на знаменатель, расположив полиномы числителя и знаменателя по убывающим степеням:

Отсюда видно, что Z_rC(p) можно представить в виде непрерывной дроби

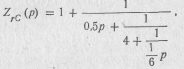
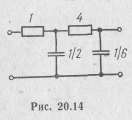
которой соответствует схема двухполюсника, приведенная на рис. 20.14.

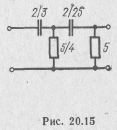
Если полиномы числителя и знаменателя расположить по возрастающим степеням, то получим

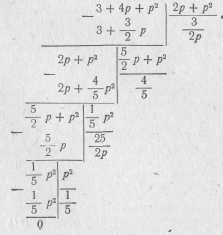
откуда видно, что Z_rC(p) можно представить в виде непрерывной дроби

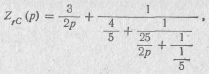
которой соответствует схема двухполюсника, приведенная на рис. 20.15.