20. Основы синтеза линейных электрических цепей

20.1. Задача синтеза электрических цепей

Задачей синтеза электрических цепей является нахождение схемы электрической цепи и параметров входящих в нее элемен­тов по заданным характеристикам цепи. Заданными характери­стиками могут быть: операторные входные или передаточные функции; амплитудно-частотная или фазо-частотная характери­стика либо обе эти характеристики одновременно; переходная или импульсная характеристика.

Операторные входные и передаточные функции, как правило, задаются их аналитическими выражениями, а остальные харак­теристики могут быть заданы как аналитически, так и в виде гра­фиков.

Процесс решения задачи синтеза можно разделить на два этапа: этап аппроксимации заданных характеристик с помощью функций, удовлетворяющих соответствующим условиям физиче­ской реализуемости, и этап реализации этих функций с помощью электрической цепи, состоящей только из пассивных элементов (резисторов, индуктивных катушек, конденсаторов и трансформа­торов), или цепи, имеющей как пассивные, так и активные эле­менты (радиолампы, транзисторы).

Под условиями физической реализуемости функций электриче­ских цепей понимают необходимые и достаточные условия, кото­рым должны удовлетворять функции, выражающие характери­стики электрических цепей. При этом под достаточностью условий понимается возможность построения хотя бы одной физически осу­ществимой цепи с характеристиками в виде заданной функции. Эти условия налагают ограничения на вид функций, которые можно реализовать с помощью электрических цепей с сосредото­ченными параметрами.

Следует отметить, что научно обоснованное проектирование электрических цепей возможно только на основе методов их син­теза. Материал, относящийся к современному синтезу цепей, весьма обширен. Поэтому ограничимся рассмотрением только основных положений метода синтеза линейных электрических це-

пей с сосредоточенными параметрами в частотной области, полу­чившего название частотного метода синтеза цепей.

Этап аппроксимации, заданных характеристик в этом методе синтеза осуществляется таким образом, чтобы по заданным харак­теристикам электрической цепи получить выражение ее оператор­ной входной или передаточной функции, удовлетворяющей усло­виям физической реализуемости.

Хотя решение конкретной задачи синтеза начинается с этапа аппроксимации, знакомство с основами синтеза удобнее начать с рассмотрения методов реализации, так как они служат базой для решения любой задачи синтеза цепей. Вначале рассмотрим методы реализации реактивных двухполюсников, предварительно установив свойства их операторных входных функций.

20.2. Входные операторные функции реактивных двухполюсников

Р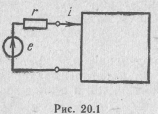 еактивными двухполюсниками называют двухполюсники, со­ставленные лишь из элементов L и С. Так как первоначально за­пасенная энергия в таких двухполюсниках не расходуется на теп­ловые потери, то процесс свободных колебаний в таких цепях носит неза­тухающий характер. Следовательно, все нули полиномов знаменателей Z(p) и Υ(ρ), а так как Z(p) = 1/Y(р), то и все нули полиномов числителей Z(p) и Υ(ρ), как показано в подразд. 18.4, должны располагаться на мнимой оси, быть простыми и сопряженными, за исключением нуля при jω=0.

При изменении р вдоль мнимой оси, т. е. при p=jω, веществен­ная часть функций Z(p) и Υ(ρ) равна нулю, так как реактивный двухполюсник не потребляет активной мощности. Мнимая часть этих функций, т. е. мнимая частотная характеристика, является нечетной функцией частоты ω. Поэтому каждую из этих функций можно представить как отношение четной функции А(р²) к нечет­ной рВ(р²) или, наоборот, как отношение нечетной функции к четной.

Для выяснения характера функций A(р²) и рВ(р²) подключим ко входным зажимам реактивного двухполюсника последовательно соединенные источник э. д. с. е и активное сопротивление r (рис. 20.1).

Входная операторная проводимость полученной цепи по отно­шению к зажимам источника э. д. с. е

. (20.1)

Входное операторное сопротивление Z(p), как было показано выше, можно представить в виде

Z (р) = A (ρ'-)/ρβ (/;-•) или . (20.2)

Подставив выражение (20.2) в формулу (20.1), получим

или

Знаменатели этих выражений являются характеристическими полиномами цепи, схема которой изображена на рис. 20.1. Так как эта цепь содержит активное сопротивление r, то процесс свобод­ных колебаний в ней будет носить затухающий характер, а следо­вательно, полиномы знаменателей (20.3) являются полиномами, нули которых расположены в левой полуплоскости р, т. е. поли­номами Гурвица.

В подразд. 18.5 было показано, что полином Гурвица можно представить в виде суммы четной и нечетной частей (18.51)

и что при умножении четной или нечетной части этого полинома на положительную постоянную величину получим новый полином, являющийся также полиномом Гурвица. Следовательно, поли­номы A(p²) и рВ(р²) являются четной и нечетной частями поли­нома Гурвица, одна из которых умножена на постоянный положи­тельный множитель r,

Таким образом, необходимым условием того, чтобы заданная функция оператора р была входной операторной функцией реак­тивного двухполюсника, является то, чтобы она была дробью, представляющей собой отношение четной и нечетной или, наобо­рот, нечетной и четной частей полинома Гурвица. Учитывая свой­ства четной и нечетной частей комплекса полинома Гурвица, уста­новленные в подразд. 18.5, можно сделать вывод о том, что нули и полюсы входной операторной функции реактивного двухполюс­ника на мнимой оси являются простыми и взаимно чередующи­мися. Такие функции называют реактансными.

Из полинома Гурвица нечетной степени n=2v+l

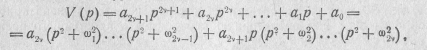
взяв отношение нечетной его части к четной и, наоборот, четной части к нечетной, получим два вида операторных входных сонро-тивлений некоторых реактивных двухполюсников:

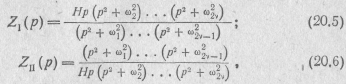
где

Аналогичным образом из полинома Гурвица четной сте­пени n=2v+2

получим

где .

Так как входная операторная проводимость обратна Z(p), то для реактивных двухполюсников она будет выражаться в виде, аналогичном (20.5) —(20.8).

В следующем подразделе покажем, что указанные выше необ­ходимые условия для функций реактивных двухполюсников яв­ляются также и достаточными.