1. Вспомогательные расчеты:

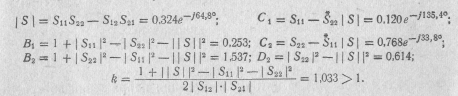
2. Максимальный коэффициент усиления

3. Для достижения максимального усиления в схеме необходимо обеспечить двухстороннее согласование, что возможно при

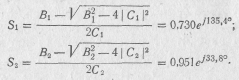
Этим коэффициентам отражения соответствуют сопротивления источника входного сигнала и нагрузки с учетом согласующих цепочек:

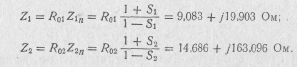
Полученные величины являются исходными для расчета параметров согла­сующих цепочек.

22.3. Применение эвм к решению задач анализа и синтеза цепей

Методы теории цепей обычно используются для решения за­дач трех типов: задач анализа, синтеза и оптимизации. Наиболее простыми являются задачи анализа. Они сводятся к составлению и решению уравнений цепи. Задачи синтеза заключаются в оты­скании схемы и ее параметров по заданным характеристикам цепи. В задачах оптимизации ставится цель такого выбора пара­метров цепи, при котором достигаются экстремальные значения той или иной ее функции, реализуются заданные характеристики, обеспечивается нужный запас устойчивости; проводится оценка влияния изменения параметров компонентов схемы на функции цепи и т. д. Для решения всех этих задач широко используются ЭВМ, которые в зависимости от принципа их работы можно раз­делить на две основные группы — ЭВМ непрерывного и дискрет­ного действия.

Работа ЭВМ непрерывного действия, или аналоговых ЭВМ, основана на моделировании математических величин непрерыв­ными физическими процессами в электронных схемах. Для иссле­дования математического выражения (например, дифференциаль­ного уравнения) на такой ЭВМ составляется и исследуется электрон­ная схема, описываемая подобным же выражением. В аналоговой ЭВМ есть комплекс электронных функциональных преобразовате­лей, устройств, выполняющих умножение, дифференцирование, интегрирование и другие действия над мгновенными значе­ниями электрических величин. С помощью этих устройств в ма­шине создаются схемы, в которых изменения напряжений во вре-

мени описываются теми же уравнениями, что и изучаемое явление. Решение уравнений получается в виде осциллограмм напряже­ний— аналогов математических величин. Аналоговые ЭВМ имеют сравнительно ограниченный диапазон применения — в основном для анализа переходных процессов, исследования систем управле­ния и регулирования, решения некоторых задач синтеза. В рамках соответствующих задач их применение очень эффективно. Прин­ципиальным недостатком таких ЭВМ является ограниченная точ­ность вычислений, определяемая погрешностью изготовления и не­стабильностью характеристик используемых элементов.

Значительно более широкий круг задач удается решать на ЭВМ дискретного действия — электронных цифровых вычисли- , тельных машинах (ЭЦВМ). Такие ЭВМ оперируют с числовыми величинами, представленными в цифровой форме. Поэтому мате­матические величины в них представляются и обрабатываются в цифровой, дискретной форме. Цифровая ЭВМ содержит про­граммно-управляемый комплекс устройств, выполняющих ариф­метические и логические операции над числами. С помощью этих операций в ЭЦВМ осуществляется преобразование числовой ин­формации. Управление этим процессом производится автоматиче­ски и в полном соответствии с заранее составленной программой. Составление программы является отдельным и часто трудоемким этапом. Основными преимуществами ЭЦВМ являются их универ­сальность и высокая точность работы.

Все задачи, встречающиеся в теории цепей, основаны на ис­пользовании математических моделей цепи в виде алгебраических, дифференциальных, разностных или других уравнений. Особен­ность их решения на ЭЦВМ заключается в необходимости сведе­ния процедуры решения к последовательности арифметических и логических операций, предусмотренных в машине. Это делается с помощью методов вычислительной математики, иначе — числен­ных методов.

Методы вычислительной математики позволяют свести к по­следовательности арифметических и логических операций, выпол­няемых на ЭЦВМ, решение всех доступных в настоящее время задач. Эффективность решения на ЭЦВМ поставленных задач за­висит от выбора методов теории цепей, предназначенных для со­здания математической модели цепи, и численных методов, необ­ходимых для решения составленных уравнений. Качество этих методов определяется удобством программной реализации (про­стотой и доступностью программирования), количеством требуе­мых для вычислений действий и достигаемой точностью вычисле­ний. Относительные достоинства различных методов и программ расчета в большой степени зависят от конкретного приложения и формулирования, постановки задачи.

При проведении расчетов электрических цепей на ЭЦВМ ис­пользуется много различных программ, простых и сложных. Одни из них позволяют проводить расчеты установившихся режимов по постоянному или переменному току, другие — анализировать пере-

ходные режимы во временной или частотной области, рассчиты­вать линейные или нелинейные цепи. Переходные процессы в ли­нейных цепях более удобно анализировать в частотной области, а в нелинейных цепях — во временной области. Это приводит к разделению программ анализа.

Применение ЭЦВМ к решению задач анализа и синтеза цепей возможно на разных уровнях. Самый низкий из них (уровень «большой логарифмической линейки») соответствует расчетам по готовым формулам, построениям таблиц и графиков. Более высо­кие уровни предусматривают использование стандартных и спе­циализированных программ математического обеспечения. Они по­зволяют в значительной степени автоматизировать весь процесс проектирования схем.

Широкое применение получили ЭЦВМ при расчете и проекти­ровании электронных схем. Применение ЭЦВМ позволило суще­ственно углубить теоретический анализ проектируемой схемы и резко сократить объем экспериментальных работ, а в результате значительно снизить сроки и стоимость, а также существенно рас­ширить возможности проектирования. В настоящее время машин­ное проектирование электронных схем, в основе которого лежат теоретические методы исследования и расчета электронных цепей с применением современных средств вычислительной техники, сложилось в отдельную область науки и техники.

Основой машинного проектирования электронной схемы яв­ляется ее машинный анализ. Важным этапом анализа цепи яв­ляется математическое описание происходящих в ней процессов. Это математическое описание включает составление эквивалент­ной схемы цепи и составление уравнений, описывающих процессы в ней.

Первоначально применение ЭЦВМ для анализа электронных схем было основано на составлении уравнений цепи вручную, а также на составлении и отладке машинных программ для каж­дого частного случая. Трудоемкость такой процедуры, необходи­мость практически заново повторять работу по программированию даже при небольшом изменении схемы показали бесперспектив­ность такого подхода.

Использование матрично-топологических методов анализа це­пей позволило полностью формализовать и осуществить с по­мощью ЭЦВМ процесс составления уравнений цепи. При этом исходными данными являются списки элементов эквивалентной схемы и значения их параметров, таблица соединений этих эле­ментов и характеристики действующих на схему сигналов. Машинные программы, реализующие алгоритмы составления систем уравнений цепи, совместно с машинными программами решения этих уравнений легли в основу универсальных программ анализа электронных схем.

Применение таких программ расширило диапазон решаемых задач и выдвинуло более жесткие и разнообразные требования к математическому описанию (математическим моделям) компо-

нентов электронных схем. Особую трудность представляет построе­ние моделей активных компонентов (полупроводниковых и других устройств). В последние годы предложено большое число разно­образных моделей активных компонентов, которые позволяют обеспечить требуемую точность математического моделирования электронных схем. На их основе с помощью универсальных про­грамм на ЭЦВМ формируется общая математическая модель всей электронной схемы, а также необходимых математических соотно­шений для решения задач анализа и синтеза.

Математическое моделирование на ЭЦВМ, под которым пони­мают имитацию условий работы реальных электрических цепей и систем с помощью вычислительных алгоритмов, реализуемых в виде машинных программ, называют цифровым моделированием. Цифровая модель может быть введена в реальную техническую систему вместо имитируемого устройства, так как алгоритм-ими­татор в ряде отношений может оказаться лучше, чем имитируемое устройство. Примерами могут служить цифровые модели филь­тров. Соответствующее таким фильтрам направление называют цифровой фильтрацией.

В универсальных программах анализа электронных схем для получения уравнений цепи нашли применение разные методы. К ним прежде всего относятся обобщенный метод узловых напря­жений (контурных токов) и метод переменных состояния. С по­мощью этих программ анализ схемы производится на основе матричной алгебры или на основе теории сигнальных графов.

Первые программы машинного анализа электронных схем (ЕСАР, NASAP, NODAL и др.) были разработаны в конце 60-х го­дов. Для получения уравнений цепи в них использовался обоб­щенный метод узловых напряжений. Однако при анализе переход-, ных процессов этот метод оказался недостаточно удобным. В об­щем случае он приводит к системам дифференциальных уравне­ний, не разрешенным относительно производных. Для решения этих уравнений нужно использовать сравнительно мало разрабо­танные методы неявного интегрирования.

Новое в составлении уравнений цепи связано с использованием так называемых переменных состояния. Как известно, состояние цепи полностью определяется ее внутренними запасами энергии и входящими в ее состав автономными источниками энергии. Пере­менными состояния называются заряд конденсаторов и потоко-сцепления катушек индуктивности, а при постоянных значениях емкостей и индуктивностей переменными состояния являются на­пряжения на емкостях и токи в индуктивностях. Метод перемен­ных состояния приводит к описанию цепи системой дифференци­альных уравнений первого порядка, разрешенных относительно производных, т. е. приведенных к нормальной форме. Это суще­ственно облегчает разработку машинных алгоритмов. Численные методы решения таких уравнений являются наиболее разработан­ными. Метод переменных состояния лег в основу многих программ машинного анализа последующего поколения (SCEPTRE,

AEDNET, АФУС, ПАЭС и др.). Этот метод позволяет анализиро­вать линейные, нелинейные и параметрические цепи.

Методы машинного проектирования электронных схем получили особое развитие с появлением интегральных схем.