21.5. Преобразование спектров сигналов в нелинейных цепях

21.5.1. Умножение частоты

Умножением частоты называют выделение в цепи с нелиней­ным элементом гармоник с частотами, кратными частоте входного сигнала, действующего на цепь. Выделение нужной частоты осу-

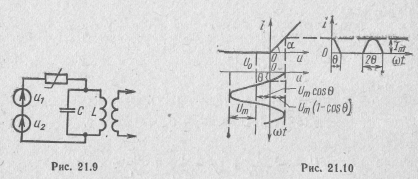
ществляется с помощью колебательного контура, настроенного на частоту выделяемой гармоники.

Умножение частоты можно осуществить с помощью различных нелинейных элементов. Наиболее часто используют диоды и триоды, как полупроводниковые, так и вакуумные.

Рассмотрим электрическую цепь с нелинейным элементом (рис. 21.9). В цепь включен колебательный контур, настроенный на частоту п-й гармоники, т. е. на частоту . На вход цепи подаются два напряжения:

и ,

т. е. синусоидальное напряжение с частотой ω₁ и постоянное на­пряжение, предназначенное для выбора рабочей точки на вольт-амперной характеристике нелинейного элемента.

Вольт-амперная характеристика нелинейного элемента аппрок­симируется двумя отрезками прямых (рис. 21.10) и аналитически записывается в виде

где a₁= tga.

Ток в цепи представляет собой последовательность видеоим­пульсов косинусоидальной формы с амплитудой I_т, длительностью τ_и=2θ/ω₁ и периодом T=2π/ω₁ где θ — так называемый угол отсечки, равный половине длительности импульса, выраженной в угловой мере. Угол отсечки зависит от амплитуды синусоидаль-

ного напряжения U_m и величины напряжения смещения U₀ (см. рис. 21.10).

Для определения амплитуд гармоник импульсов тока получим вначале аналитическую запись для импульсов тока. Так как U₀ = U_mcosθ (см. рис. 21.10), то

При этом .

При ω₁t = 0 ток

,

откуда

a₁=I_m/U_m(1-cosθ).

Подставив это в выражение для i, получим

i=I_m(cosω₁t-cosθ)/(l -cosθ). (21.10)

Для определения амплитуды n-й гармоники воспользуемся формулой для вычисления коэффициентов ряда Фурье в тригоно­метрической форме

Подставив сюда выражение (21.10), получим

Воспользовавшись соотношением , после интегрирования будем иметь

Отношение амплитуды n-й гармоники I_тп к амплитуде импуль­сов тока I_m называют коэффициентом n-й гармоники:

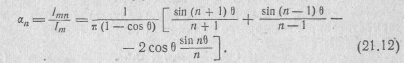
Графики зависимостей коэффициентов гармоник а_п от угла от­сечки θ (рис. 21.11) называют по имени советского ученого А. И. Берга, впервые предложившего этот способ расчета коэффи­циентов гармоник, кривыми Берга.

Из этих зависимостей видно, что для каждой гармоники имеется свой оптимальный угол отсечки, при котором ее амплитуда становится максимальной. Например, для первой гармоники θ_ОПТ= 120°, для второй θ_ОПТ = 60° и т. д. С помощью этого графика

можно выбирать угол отсечки, необходимый для получения макси­мальной амплитуды желаемой гармоники.

Графики спектров сигналов на входе и выходе цепи при умно­жении частоты приведены на рис. 21.12.

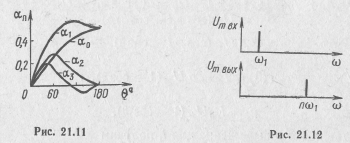
21.5.2. Преобразование частоты (гетеродинирование)

Преобразованием частоты {гетеродинированием) называют та­кое нелинейное преобразование сигналов, при котором из сигна­лов двух различных частот ω₁ и ω₂ выделяется сигнал разностной частоты ω_пр=|ω₁— ω₂|. Такое преобразование широко исполь­зуется для понижения несущей частоты сигналов, подлежащих дальнейшему усилению, например в супергетеродинных радиопри­емниках. В этом случае под ω₁ следует понимать несущую ча­стоту ω₀, а под ω₂ — частоту местного генератора (гетеродина) ω_г. Величину ω_г выбирают так, чтобы разность (ω₀— ω_г) была для всех несущих частот одинаковой. Эту постоянную разностную ча­стоту называют промежуточной частотой.

Преобразование частоты используется также в измерительной технике, в эталонных генераторах и в ряде других устройств.

Преобразование частоты можно осуществить в схеме с нели­нейным элементом (см. рис. 21.9), где u₁ = U_ml sin ω₁t, u₂ = U_m2 sin ω₂t. резонансная частота контура ω ₀ = ω _пр = | ω₁- ω₂|= , а вольт-амперная характеристика нелинейного элемента аппроксимируется полиномом второй степени

i = а₀ + a₁u + a₂u². (21.13)

Ток в такой цепи

Используя соотношения

после преобразования получим

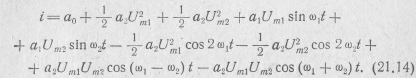
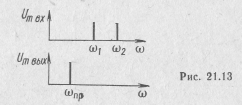
Частоты носят название, простых комбинационных ча­стот. Составляющая тока разностной частоты

будет создавать на контуре, настроенном на эту частоту, падение напряжения. Остальные компоненты будут шунтироваться кон­туром.

Графики спектров сигналов на входе и выходе цепи при преоб­разовании частоты приведены на рис. 21.13.