20.14. Понятие о синтезе пассивных и активных rС-фильтров

В последние годы в связи с развитием микроэлектроники резко возрос интерес к проектированию селективных цепей, состоящих из сопротивлений, емкостей и транзисторов. Уже в настоящее

время rC-фильтры по большинству показателей начинают успешно конкурировать с обычными LC-фильтрами, особенно в диапазоне низких и инфранизких частот.

Следует отметить, что, по крайней мере теоретически, возмож­ности получения требуемых характеристик у цепей rС не хуже, чем у цепей LC. Однако для обеспечения высокой избирательно-

сти пассивные rC-фильтры требуют большого числа элементов и громоздких схемных структур. Поэтому в настоящее время наи­большее распространение получили активные rC-фильтры, в кото­рых обеспечивается высокая, избирательность при достаточно ма­лой массе и габаритах.

Методика синтеза пассивных rC-фильтров, изложенная, напри­мер, в [23], основывается на каскадном включении звеньев фильтра и пренебрежении влиянием последующих звеньев на характери­стики предыдущих. Для обеспечения этого необходимо между от­дельными звеньями ставить развязывающие усилители или же по­вышать уровень входного сопротивления каждого последующего звена, т. е. входное сопротивление каждого последующего звена делать более высокоомным.

Передаточную функцию полиномиального пассивного rC-фильтра нижних частот выбирают равной

К(р) = 1/(1+δ₁р)^п. (20.72)

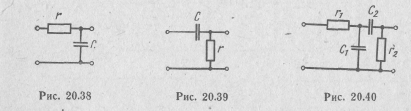
Эта функция реализуется в виде каскадного включения про­стейших звеньев фильтра нижних частот (рис. 20.38), полюсы пе­редаточных функций которых p₁ = -1/δ₁ являются кратными. Ко­личество звеньев п и величина б выбираются исходя из условий задачи на расчет фильтра [23].

Переход от фильтров нижних частот к фильтрам верхних ча­стот и полосовым фильтрам осуществляют с помощью преобразог вания частоты. Звено фильтра верхних частот приведено на рис. 20.39, а звено полосового фильтра — на рис. 20.40.

Вопросам синтеза активных rC-фильтров посвящено очень большое количество работ. Так как с помощью активных rC-цепей можно реализовывать передаточные функции с комплексными по­люсами, т. е. такие же функции, как и с помощью rLC-цепей, то задача аппроксимации при синтезе активных rC-фильтров ре­шается точно так же, как и при синтезе LC-фильтров,

Для улучшения стабильности характеристик реализацию ак­тивных rC-фильтров осуществляют, как правило, в виде каскад­ного включения отдельных звеньев с передаточными функциями не выше второго порядка.

Из многообразных методов и схем реализации звеньев актив­ных rC-фильтров наибольшее распространение в настоящее время получили схемы с усилителями, имеющими конечный коэффи­циент усиления, и схемы с операционными усилителями. Методика

реализации звеньев второго порядка для фильтров нижних ча­стот рассмотрена в подразд. 20.11. Звенья первого порядка реали­зуются, как правило, в виде пассивной rC-цепи. Порядок реали­зации многозвенного активного rC-фильтра рассмотрим на при­мере.

Пример 20.14.

Реализовать фильтр нижних частот третьего порядка, если его амплитудно-частотная характеристика аппроксимирована по Тейлору.

Решение. Учитывая, что полином Баттерворта третьего порядка (20.67) имеет вид

.

для передаточной функции фильтра по напряжению получим

. Звено с передаточной функцией K₁(p) = 1/(p+ 1) реализуем с помощью пас­сивной rC-цени (см. рис. 20.38) Сравнивая выражение передаточной функции этой цени К(р) = 1/(l+pCr) с заданной, найдем нормированные значения эле­ментов: r=1, С=1,

Звено с передаточной функцией К₂(р) = 1/(р²+р+1) реализуем активной rC-цепью с операционным усилителем, схема которой приведена на рис. 20.30. Значения элементов этой схемы получены в примере 20.11.

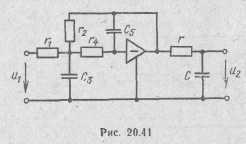
Подключив звено первого порядка к выходу операционного усилителя звена второго порядка, получим схему искомого фильтра третьего порядка, показан­ную на рис. 20.41.

Схемы реализации звеньев фильтра верхних частот и полосо­вого фильтра с усилителями, имеющими конечный коэффициент усиления, приведены на рис. 20.42 и 20.43.

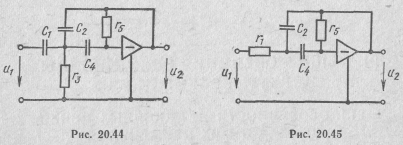
На рис. 20.44 показана схема фильтра верхних частот, а на рис. 20.45—схема полосового фильтра с операционными усили­телями.

Более подробно методика синтеза активных rC-фильтров изло­жена, например, в [13, 23, 30, 38, 62, 63].

21. ОБЩИЕ СВЕДЕНИЯ О НЕЛИНЕЙНЫХ

ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

21.1. ОСОБЕННОСТИ НЕЛИНЕЙНЫХ

ЦЕПЕЙ И ОБЛАСТИ ИХ ПРИМЕНЕНИЯ

Как уже указывалось в разд.1, нелинейной электрической цепью называют цепь, электрическое сопротивление, индуктив­ность или емкость хотя бы одного из участков которой зависит от значений или направлений токов и напряжений на этом участке цепи.

Физические процессы, протекающие в нелинейных электриче­ских цепях, описываются нелинейными алгебраическими или диф­ференциальными уравнениями, т. е. уравнениями, которые содер­жат нелинейные функции тока, напряжения и их производных, на­пример, ток и напряжение в степенях выше первой или с коэффи­циентами, зависящими от тока или напряжения.

Нелинейные цепи имеют следующие основные особенности:

1. К ним неприменим принцип наложения. Рассмотрим это на примере нелинейного элемента, в .котором ток пропорционален квадрату напряжения: i=au².

Если в цепи действуют одновременно два последовательно включенных источника напряжения и₁ и и₂, то ток в цепи

.

Этот ток не равен сумме токов, вызываемых в цепи действием каждого источника в отдельности:

.

2. В отличие от линейных цепей в нелинейных цепях в устано­вившемся режиме при синусоидальном входном воздействии вы­ходная величина будет несинусоидальной, т. е. на выходе цепи появляются гармонические составляющие частот, не содержа­щиеся во входном воздействии. Преобразование спектра частот — одна из характерных особенностей нелинейных цепей.

3. В отличие от линейных электрических цепей, в которых за­висимость между током и напряжением (вольт-амперная характе-

ристика), зависимость заряда конденсатора от приложенного к нему напряжения (кулон-вольтная характеристика) и зависи­мость потокосцепления индуктивного элемента от тока (вебер-ам-перная характеристика) являются линейными, в нелинейных цепях

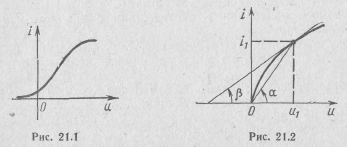
эти зависимости нелинейны. Пример нелинейной вольт-амперной характеристики приведен на рис. 21.1.

4. В нелинейных электрических цепях в отличие от линейных для характеристики элементов вводят так называемые статиче­ские и динамические параметры.

Статическим сопротивлением назы­вают отношение постоянного напряже­ния на элементе к установившемуся значению постоянного тока:

r_c(i) = u/i.

О но пропорционально котангенсу угла наклона линии, проведенной в рассматриваемую точку вольт-ампер­ной характеристики нелинейного эле­мента из начала координат (рис. 21.2).

Динамическим сопротивлением нелинейного элемента назы­вают производную от напряжения на этом элементе по току в нем:

,

Оно пропорционально котангенсу угла наклона касательной в рассматриваемой точке вольт-амперной характеристики (см. рис. 21.2) и может быть как положительным, так и отрицательным

(рис. 21.3).

Статические и динамические параметры вводят также и для нелинейных индуктивностей и емкостей.

Нелинейные цепи находят большое применение во многих электротехнических устройствах. Ряд необходимых преобразова­ний токов и напряжений возможно осуществить только в нелиней­ных электрических цепях. Такими преобразованиями являются:

преобразование переменного тока в постоянный, т. е. выпрям­ление;

генерирование синусоидальных и релаксационных колебаний, т. е. преобразование постоянного тока в переменный синусоидаль­ный или несинусоидальный;

модуляция, т. е. изменение амплитуды, частоты или фазы вы­сокочастотного колебания в соответствии с законом изменения управляющего сигнала;

демодуляция или детектирование, т. е. выделение полезного управляющего сигнала из модулированных высокочастотных ко­лебаний;

преобразование частоты, τ. е. изменение несущей частоты сигнала с сохранением закона модуляции;

умножение и деление частоты;

стабилизация напряжения и тока;

построение математических функций и ряд других преобразо­ваний.

Большинство из названных выше преобразований рассматри­вается в инженерно-технических дисциплинах. Здесь же ограни­чимся рассмотрением общих сведений о нелинейных элементах, об аппроксимации их характеристик, о методах расчета нелиней­ных цепей и преобразовании спектров сигналов в нелинейных цепях.