20.13.2. Синтез фильтров нижних частот с аппроксимацией их амплитудно-частотных характеристик по Чебышеву

При аппроксимации амплитудно-частотной характеристики фильтра нижних частот по Чебышеву квадрат этой характеристики представляют в виде

где ε — коэффициент, определяющий неравномерность амплитуд­но-частотной характеристики в полосе пропускания фильтра;

P_n(Ω) —полином Чебышева степени п от нормированной частоты Ω = ω/ω_C

В качестве примера на рис. 20.36 приведен график |K(j Ω)|² при n=4. Из этого графика видно, что отклонения квадрата амп­литудно-частотной характеристики в полосе пропускания фильтра от единицы имеют волновой характер. Поэтому рассматриваемую

аппроксимацию часто называют равноволновой. В полосе задержи­вания кривая зависимости |K(jΩ)| монотонно убывает с увеличе­нием частоты.

Для определения операторной передаточной функции филь­тра К(р) по аппроксимирующей функции |K(jΩ)|² в выраже­нии (20.68) произведем замену jΩ = σ.

П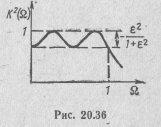 ри этом получим

. (20.69)

Полюсами этой функции являются корни уравнения

,

которые равны [47]

p_k=σ_k+jω_k,

где

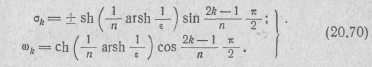
Так как коэффициент при старшем члене знаменателя (20.68) равен ε²(2^n-1)², то искомая операторная передаточная функция фильтра будет иметь вид

Эта функция реализуется реактивным четырехполюсником, со­держащим η реактивных элементов.

Порядок расчета фильтра нижних частот с аппроксимацией его амплитудно-частотной характеристики по Чебышеву рассмотрим на конкретном примере.

Пример 20.13.

Произвести расчет нормированного фильтра нижних частот по заданным в предыдущем примере требованиям к нему. Значение амплитудно-частотной характеристики фильтра в полосе пропускания должно быть не меньше 0,707, а ее аппроксимацию произвести по Чебышеву.

Решение.

В соответствии с уравнением (20.69) для амплитудно-частотной характери­стики на границе полосы пропускания фильтра можно записать

,

откуда можно найти ε=1.

Для определения степени полинома Чебышева я воспользуемся выражением (20.69). Подставив в него найденное значение е и учтя заданные условия для полосы задерживания, получим

,

откуда Р_n(2) 10.

Воспользовавшись выражениями для полиномов Чебышева (подразд. 20.12), находим P₂(2)=7 и Р₃(2)=26. Следовательно, необходимо выбрать n = 3.

Воспользовавшись выражением (20.70), найдем полюсы передаточной функ­ции: p_l=-0,3; р_2,3=- 0,15±j0,87.

Подставив эти значения в формулу (20.71), получим выражение для пере­даточной функции

Так как числитель полученного выражения является четной функцией, то, разделив четную часть знаменателя на его нечетную часть, получим параметр Y₂₂ синтезируемого четырехполюсника:

.

Разложение этой функции в цепную дробь дает:

Рис. 20.37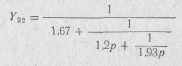

Этой дроби соответствует реактивный четырехполюсник, схема которого приведена на рис. 20.37.

Нормированные значения его элементов равны: L₁=1,93; C_l = 1,2; L₂=l,67; r_H=l.

Рассмотренные примеры синтеза фильтров с аппроксимацией их амплитудно-частотных характеристик по Тейлору и Чебышеву показывают, что для удовлетворения одинаковых требований к амплитудно-частотным характеристикам фильтр с аппроксима­цией по Чебышеву получается менее сложным, так как содержит меньшее число элементов, чем фильтр с аппроксимацией по Тей­лору. Однако фазо-частотные характеристики фильтров с аппрок­симацией по Чебышеву менее линейны, чем фильтров с аппрокси­мацией по Тейлору. Поэтому если не предъявляется особых тре­бований к линейности фазо-частотных характеристик, то целесо­образно применять аппроксимацию по Чебышеву, а если такие требования предъявляются, то применяют аппроксимацию по Тейлору.

Кроме рассмотренных, применяются и другие виды аппрокси­мации [9, 32].

В заключение следует отметить, что расчет фильтров по рабо­чим параметрам требует значительной по объему вычислительной работы. Расчеты существенно усложняются, если их вести с уче­том потерь в элементах фильтра. Поэтому в последнее время при синтезе электрических фильтров стали широко применяться элек­тронные вычислительные машины.