20.12. Задача аппроксимации в проблеме синтеза электрических цепей

Синтез электрических цепей, как указывалось в подразд. 20.1, связан с решением двух задач: аппроксимации и реализации.

Задача аппроксимации состоит в нахождении функции F(x) переменного х, удовлетворяющей условиям физической реализуе­мости, которая с необходимой точностью воспроизводила бы за­данную функцию ξ(x) в требуемом интервале х. Этой заданной функцией ξ(x) может быть амплитудно-частотная, фазо-частотная или одна из временных характеристик электрической цепи (пере­ходная h(t) или импульсная a (t) характеристики). Эти характери­стики могут быть заданы аналитически или графически. Если за­данной является одна из временных характеристик, то эту харак­теристику можно преобразовать по Лапласу в функцию частоты. Однако задаваемая степень приближения при аппроксимации вре­менной функции переводится в степень приближения по частоте с большими трудностями вычислительного характера. Поэтому если заданными являются временные характеристики, то синтез электрической цепи целесообразно производить не в частотной, а во временной области [2, 27].

Задача аппроксимации решается с привлечением методов ин­терполирования и приближения функций, которые излагаются в высшей математике. Здесь же ограничимся кратким рассмотре­нием аппроксимации в виде «гладкой» кривой (аппроксимации по

Тейлору) и наилучшего (равномерного) приближения (аппрокси­мации по Чебышеву), которые находят широкое применение при синтезе электрических цепей.

20.12.1. Аппроксимация по Тейлору

Ф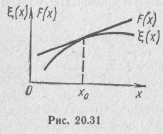 ункция Р(х) является аппроксимирующей функцией п-то по­рядка по Тейлору относительно функции ξ(x) (рис. 20.31), если в точке х=х₀ равны значения этих функций и n—1 производных

младших порядков, т. е.

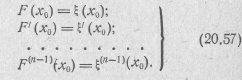
Погрешность рассматриваемой аппроксимации F(x)—ξ(x) можно найти, если каждую из функций представить рядом Тейлора:

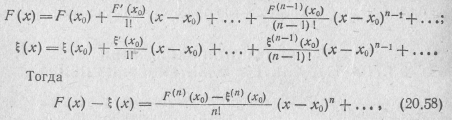
т. е. при аппроксимации по Тейлору первые n—1 производных функций отклонения F(x)—ξ(x) при х=х₀ равны нулю. С увели­чением разности х—x₀ отклонение увеличивается. Следовательно, рассматриваемая аппроксимация описывает заданную функцию наиболее точно при значениях х, близких к x₀, и менее точно при значениях х, значительно отличающихся от х₀.

20.12.2. Аппроксимация по Чебышеву

Функция F(x) аппроксимирует по Чебышеву функцию ξ(x), если эта функция выбрана таким образом, что наибольшее значе­ние модуля разности |F(x)—ξ(x)| -- интервале приближения является минимальным.

Этот тип аппроксимации назван по имени русского математика академика П. Л. Чебыщева (1821—1894 гг.), который впервые сформулировал и указал общие методы решения задачи наилучшего приближения функций. Теория наилучшего приближения функций, основанная П. Л. Чебышевым, была блестяще развита в работах наших соотечественников Е. И. Золотарева, П. И. Ахиезера и др.

При решении задач наилучшего приближения функций большое применение находят так называемые полиномы Чебышева, которые вычисляются по формуле

Р_п (х) = cos (n arccos x). (20.59)

При п=1 получим

Р₁ (х) = cos (arccos x) = x.

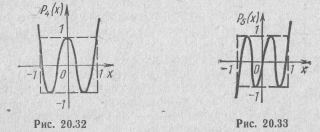
При n=2

При n=3; 4; 5 эти полиномы имеют вид:

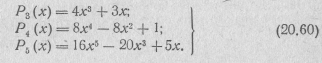
Из приведенных выражений видно, что полиномы Чебышева представляют собой многочлены степени п с коэффициентом при старшем члене, равным 2^n-1. В качестве примера на рис. 20.32 и 20.33 приведены графики полиномов Р₄(х) и Р₅(х).

Особенностью полиномов Чебышева является то, что в интер­вале они из всех полиномов степени п с коэффициен­том при старшем члене 2^п-] наименее отклоняются от нуля. Вне указанного выше интервала значения этих полиномов по абсолют­ной величине являются наибольшими из всех полиномов степени n.