19. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

19.1. ПОНЯТИЕ ОБ ОБРАТНОЙ СВЯЗИ

В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

И МЕТОДАХ АНАЛИЗА ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮ

О братные связи очень широко распространены как в природе, так и в технике. Применительно к электрическим цепям обратная связь проявляется,в воздействии выходной величины электриче­ской цепи на ее вход, благодаря чему создается замкнутая цепь зависимо­стей между входными и выходными величинами электрической цепи.

В качестве примера электрической цепи с обратной связью на рис. 19.1 приведена схема однокаскадного элек­тронного усилителя, в котором обрат­ная связь осуществляется путем по­дачи части выходного напряжения с делителя, состоящего из сопротивле­ний r₁ и r₂, на вход усилителя.

Элемент или группу элементов, по­средством которых осуществляется об­ратная связь, называют цепью обрат­ной связи. В приведенном на рис. 19.1 усилителе цепью обратной связи является делитель напряжения r₁ и r₂.

Примененную в рассматриваемом усилителе обратную связь иногда называют внешней обратной связью. Такая обратная связь вводится в электрическую цепь специально в целях улучшения ее некоторых характеристик. Кроме специально вводимых, обратные связи в электрических цепях могут возникать самопроизвольно, например за счет междуэлектродных емкостей электронных при­боров. Такие связи называют внутренними. Эти связи могут ока­зывать вредное влияние на электрические цепи, например могут приводить к самовозбуждению усилителей, в результате которого они перестают выполнять свои функции усиления подводимых к ним полезных сигналов. В этом случае принимают меры по устранению или уменьшению этих связей,

Если напряжение обратной Связи пропорционально напряже­нию на выходе цепи, как, например, в приведенном на рис. 19.1 усилителе, то обратную связь называют обратной связью по напряжению. Если напряжение обратной связи пропорционально току на выходе цепи, то ее называют обратной связью по току. Может быть и комбинированная обратная связь — и по току, и по напряжению.

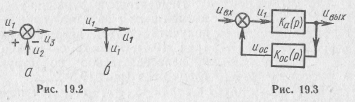
Анализ электрических цепей с обратной связью, содержащих электронные лампы и транзисторы, можно производить с помощью рассмотренных в разд. 12 общих методов анализа активных цепей. Однако для более четкого выяснения влияния обратной связи на свойства цепи более предпочтительным методом анализа цепей с обратными связями является метод сигнальных графов. С этой же целью для анализа цепей с обратными связями часто исполь­зуют так называемый метод структурных схем, сущность которого состоит в том, что схему электрической цепи представляют в виде однонаправленных четырехполюсников, не нагружающих друг друга, т. е. таких четырехполюсников, передаточные функции ко­торых не изменяются в зависимости от того, присоединен к их за­жимам последующий четырехполюсник или нет. Эти четырехпо­люсники соединяются не двумя, а одной линией, на которой стрелкой указывают направление передачи сигнала. Внутри че­тырехполюсников обычно указывают их передаточные функции. Сложение или вычитание сигналов изображают сумматорами (рис. 19.2,а). Разветвление сигналов обозначают точкой, которую обычно называют узлом (рис. 19.2,6). Изображенную таким спо­собом схему электрической цепи называют структурной схемой.

Структурная схема простейшей электрической цепи с обратной связью приведена на рис. 19.3, где K_a(p) = U_ВЫХ(p)/U₁(p) — пере­даточная функция активного четырехполюсника без обратной связи; K_OC(р) = U_OC(р)/U_вых(р)—передаточная функция цепи об­ратной связи.

От структурной схемы цепи можно перейти к ее сигнальному графу, и наоборот, так как они отличаются друг от друга только формально. Так, заменив в структурной схеме цепи однонаправ­ленные четырехполюсники линиями с указанием их передаточных функций, получим сигнальный граф цепи. И наоборот, от сигналь­ного графа цепи можно перейти к ее структурной схеме, изобра­зив его ветви однонаправленными четырехполюсниками.

В качестве примера на рис. 19.4 показан сигнальный граф цепи, структурная схема которой изображена на рис. 19.3.

П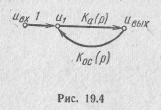 ри преобразовании структурных схем используют такие же правила, как и при преобразовании сигнальных графов, т. е. ме­тод структурных схем и метод сиг­нальных графов являются разно­видностями одного и того же ме­тода.

Передаточную функцию рассматри­ваемой цепи с обратной связью можно получить по ее сигнальному графу (рис. 19.4). Однако ее можно найти и непосредственно по структурной схеме цепи (рис. 19.3). Учитывая, что и₁ = и_BX+и_ос или u_bx=u₁-u_OC, для передаточ­ной функции цепи с обратной связью получим

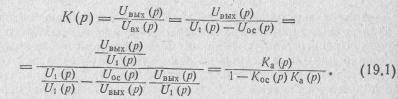
Произведение К_OC(р)К_a(р), стоящее в знаменателе этого вы­ражения, называют возвратным отношением. Оно представляет собой передаточную функцию разомкнутой петли обратной связи, равную отношению изображения выходной величины цепи обрат­ной связи U_OC(p) к изображению входной величины зависимого источника U₁(р).

Знаменатель выражения (19.1) 1—К_OC(р)К_a(р) называют возвратной разностью. Эта разность характеризует влияние обрат­ной связи на свойства цепи. Модуль этой разности называют глу­биной обратной связи. Если |1—К_OC(р)К_a(р)|>>1, то обратную связь называют глубокой. При этом выражение (19,1) можно за­писать в виде

т. е. при глубокой обратной связи передаточная функция цепи определяется только параметрами цепи обратной связи.

Если сигнал на выходе цепи обратной связи и_ос совпадает по фазе с сигналом на входе цепи u_вх, то обратную связь считают положительной; если эти сигналы находятся в противофазе,— отрицательной. Если возвратное отношение К_OC(р)К_a(р) является функцией частоты, то сдвиг фаз между и_ос и u_вх может быть отли­чен от 0 и π. В этом случае обратную связь считают положитель­ной, если модуль передаточной функции цепи с обратной связью |K(р)| будет больше модуля передаточной функции цепи без об-

ратной связи |K(р)|. Если же |К(р|<|К_а(р)|, то обратную связь считают отрицательной.

Структурная схема цепи с обратной связью для более общего случая показана на рис. 19.5. Здесь звено с передаточной функ­цией учитывает прохождение сигнала

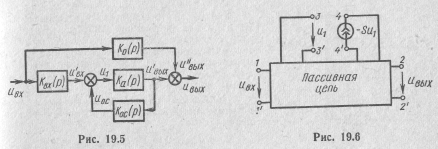
со входа цепи на ее выход через пассивную часть цепи. Звено с передаточной функцией K_BX(p) = U'_BX(p)/U_BX(p) учитывает прохождение сигнала от входа цепи ко входу зависимого источ­ника.

Передаточная функция всей цепи с обратной связью в рассмат­риваемом случае определяется выражением

Для удобства определения передаточных функций отдельных звеньев цепи с обратной связью целесообразно выделить из нее идеальный зависимый источник тока или э. д. с., а остальную часть цепи представить в виде пассивного восьмиполюсника, отнеся к нему пассивные элементы эквивалентной схемы зависимого источника. На рис. 19.6 приведена такая схема с зависимым источником тока.

Для определения передаточных функций К_BX(р) и K₀(p) ко входным зажимам цепи (рис. 19.6) необходимо подключить источ­ник напряжения u_BX, принять S=0 и найти U₁(p) и u_вых(р). При этом получим К_BX(р) = U₁(p)/U_BX (р); К₀(р) = U_выx(p)/U_BX (p).

Для определения передаточной функции цепи обратной связи К_OC(р) к выходным зажимам цепи необходимо подключить источ­ник напряжения ы_вых, принять S = 0, а ко входным зажимам цепи подключить внутреннее сопротивление источника входного сиг­нала. При этом u_l = и_ос и K_ос(р) =U₁(p)/U_ВЫХ(p).

Для определения передаточной функции К_a(р) необходимо разомкнуть цепь обратной связи левее зажимов 3—3', подклю­чить к этим зажимам напряжение и₁, а ко входным зажимам цепи 1—1' подключить внутреннее сопротивление источника вход­ного сигнала, тогда К_а (р) = U_ВЫХ(p)/U₁(p).

Методику анализа электрических цепей с обратной связью с по­мощью структурных схем рассмотрим на конкретных примерах.

Пример 19.1.

Составить структурную схему усилителя, схема которого приведена на рис. 19.1, и найти его передаточную функцию но напряжению.

Решение.

Учитывая, что сопротивления емкостей С_к, С_а и С_р для переменной составляющей вход­ного сигнала малы, схему усилителя по пере­менной составляющей входного сигнала можно представить в виде, показанном на рис. 19.7. Эту схему представим в виде эквивалентной схемы, приведенной на рис. 19.8.

Подключив ко входным зажимам цепи источник напряжения и_вх и приняв S= 0, по­лучим

Подкчючив к выходным зажимам цепи источник напряжения u_ВЫХ, приняв S = 0 и замкнув накоротко входные зажимы цени, получим

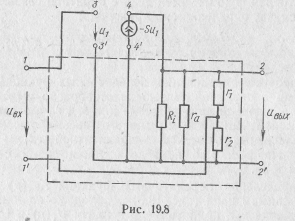
Разомкнув цепь обратной связи левее зажимов 3—3', подключив к этим зажимам источник напряжения u₁ и замкнув накоротко входные зажимы цепи, получим

При этом структурная схема усилителя будет иметь вид, показанный на рис. 19.3, а его передаточная функция будет определяться выражением

В рассмотренном примере напряжение на выходе цепи обрат­ной связи и_ос находится в противофазе с напряжением на входе усилителя и_вх, так как возвратное отношение К_OC(р)/К_а(р) яв­ляется вещественным отрицательным. Поэтому обратная связь

в этом усилителе является отрицательной. Она уменьшает модуль передаточной функции усилителя, что видно из полученных выра­жений для К(р) и K_а(Р).

Пример 19.2.

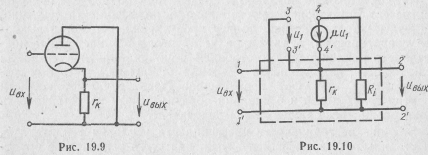
Найти передаточную функцию катодного повторителя, схема которого по переменной составляющей входного сигнала показана на рис. 19.9.

Решение.

Представив триод эквивалентной схемой с зависимым источником э. д. с., получим схему катодного повторителя, приведенную на рис. 19.10.

Подключив ко входным зажимам цепи источник напряжения u_ВХ и приняв μ=0, получим

Подключив к выходным зажимам цепи источник напряжения u_ВЫХ, приняв μ =0 и замкнув накоротко входные зажимы цепи, получим

Разомкнув цепь обратной связи перед зажимами 3—3', подключив к этим зажимам источник напряжения и₁ и замкнув накоротко входные зажимы цепи, получим

Подставив найденные значения передаточных функций в формулу (19.3), получим передаточную функцию катодного повторителя

Из рассмотренного примера видно, что катодный повторитель представляет собой усилитель напряжения с отрицательной об­ратной связью, коэффициент усиления которого меньше еди­ницы.

19.2. Влияние обратной связи на характеристики цепи

Обратная связь влияет не только на коэффициент усиления усилителя, что было показано в предыдущем подразделе, но и на другие его характеристики: стабильность коэффициента усиления, частотные характеристики, полосу пропускания, входное и выход­ное сопротивления, а также на устойчивость. В настоящем под­разделе ограничимся рассмотрением влияния обратной связи на стабильность коэффициента усиления усилителя, частотные ха­рактеристики и полосу пропускания. Понятие об устойчивости электрических цепей и о влиянии обратной связи на устойчивость будет рассмотрено в следующем подразделе.

Влияние нестабильности коэффициента усиления усилителя k_a на стабильность коэффициента усиления этого усилителя с обрат­ной связью k характеризуют так называемой чувствительно­стью , под которой понимают отношение относительного из­менения величины k к относительному изменению величины k_a:

Считая, что структурная схема усилителя с обратной связью имеет вид, показанный на рис. 19.3, и что K_a(p)=k_a, а К_OC(р) = — k_oc, в соответствии с формулой (19.1) получим

Подставив это в выражение (19.4), будем иметь

Из этого выражения видно, что отрицательная обратная связь (|1 — k_ak_oc|>1) улучшает стабильность коэффициента усиления, а положительная обратная связь (|1-k_ak_oc|<1), наоборот, ухуд­шает стабильность этого коэффициента. Поэтому отрицательная обратная связь находит широкое применение в целях улучшения стабильности коэффициента усиления, хотя при этом величина ко­эффициента усиления и уменьшается.

Для улучшения стабильности коэффициента усиления иногда применяют глубокую отрицательную обратную связь (|k_ak_oc|>>1). При этом, как следует из формулы (19.2), стабильность коэффици­ента усиления усилителя с обратной связью зависит только от стабильности цепи обратной связи. Стабильность этой цепи обычно выше стабильности коэффициента усиления усилителя, так как цепь обратной связи, как правило, выполняется из пассивных эле­ментов, параметры которых более стабильны, чем параметры ламп и транзисторов,

При оценке влияния обратной связи на частотные характери­стики и полосу пропускания цепи будем считать, что комплексные передаточные функции прямой цепи и цепи обратной связи (см. рис. 19.3) имеют вид:

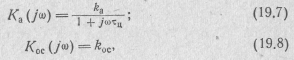
т. е. прямая цепь является апериодическим звеном, а передаточная функция цепи обратной связи равна постоянной величине, не за­висящей от частоты. Такую обратную связь иногда называют жесткой обратной связью.

Подставив выражения (19.7) и (19.8) в уравнение (19.1), по­лучим выражение для передаточной функции цепи с обратной связью:

где

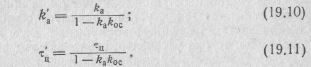
Из этих выражений видно, что при охвате апериодического звена жесткой обратной связью его структура сохраняется, т. е. оно остается апериодическим звеном. Однако его параметры — коэффициент усиления k_a и постоянная времени τ_ц — изменяются. При отрицательной обратной связи они уменьшаются, а при по­ложительной — увеличиваются.

Рассмотрим, как это влияет на амплитудно-частотную харак­теристику и полосу пропускания цепи.

В соответствии с формулой (19.7) выражение для амплитудно-частотной характеристики цепи с обратной связью имеет вид

Полосу пропускания цепи найдем из соотношения

откуда

Г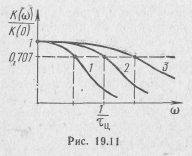 рафик нормированной амплитудно-частотной характеристики цепи приведен на рис. 19.11 (1—для цепи с положительной об­ратной связью; 2 — для цепи без обратной связи; 3 — для цепи с отрицательной обратной связью). Из этого рисунка видно, что положительная обратная связь уменьшает, а отрицательная — уве­личивает полосу пропускания рас­сматриваемой электрической цепи. Поэтому для увеличения полосы пропускания цепи и для улучше­ния равномерности ее амплитудно-частотной характеристики часто ис­пользуют отрицательную обратную связь.