Тема 6.

1. Что называется суммой сходящегося степенного ряда?

2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное число его членов?

3. Можно ли утверждать, что ряд сходится, если предел его общего члена равен нулю?

4. Сформулируйте признак Даламбера и интегральный признак Коши сходимости ряда. Сформулируйте теорему сравнения рядов.

5. Какие знакопеременные ряды называются абсолютно сходящимися и какие - условно сходящимися? Сформулируйте признак Лейбница.

6. Приведите примеры степенных рядов, имеющих нулевой, конечный и бесконечный радиус сходимости.

7. Выпишите разложения в ряд Маклорена функций: , .

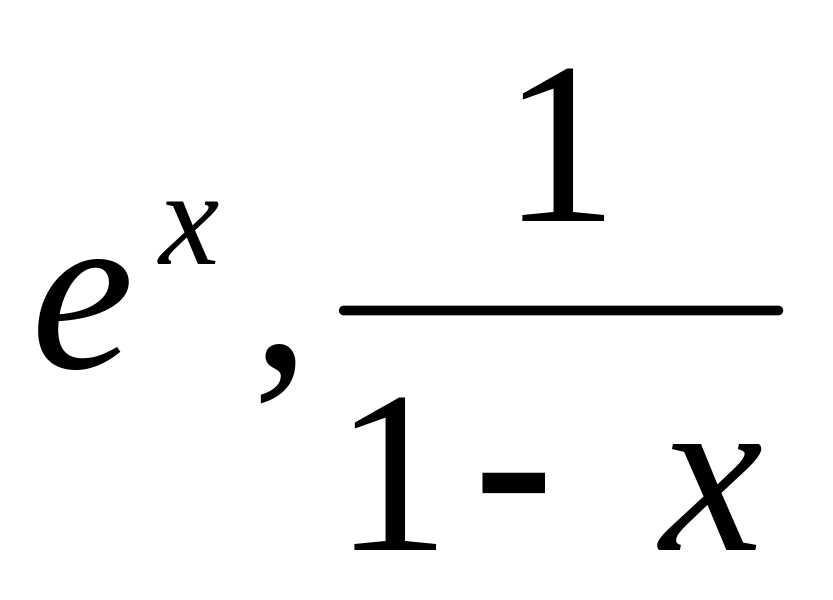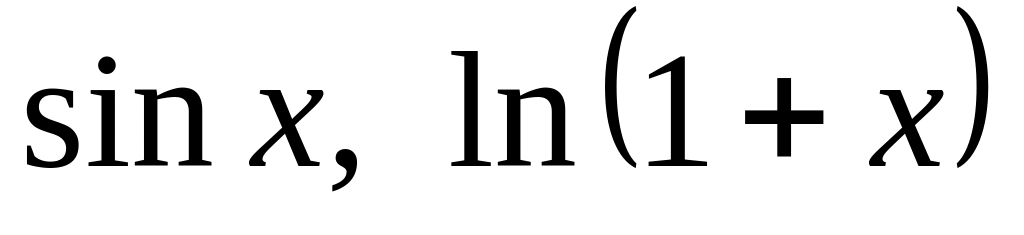Каковы области сходимости получившихся рядов?

Рекомендуемая литература

Базовые учебники:

1. Высшая математика. Базовый курс. Учебное пособие для бакалавров / Шипачев В.С. – М.: Юрайт, 2012.

2.  Краткий курс высшей математики: Учебное пособие для вузов / Б. П. Демидович, В. А. Кудрявцев. - М.: АСТ Астрель, 2004.

Основная литература:

1. Высшая математика / В. С. Шипачев. - Учебник для вузов. - М.: Высшая школа, 2003.

2. Высшая математика. Сборник задач. Часть 1.: Учебное пособие / Опарин Н.П., Югова С.Б. – ПИ (ф) ГОУ ВПО «РГТЭУ»: Изд-во «ОТ и ДО», 2011.

3. Кремер Н.Ш. Высшая математика для экономистов. – М.: ЮНИТИ, 2002.

4. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах, 2008.

Дополнительная литература:

1. Данко п.Е., Попов а.Г., Кожевников т.Я. Высшая математика в упражнениях и задачах (в 2-х частях), 6-е изд., испр. И доп.— m.: Высшая школа, 2006.

2. Гмурман В.Е. Теория вероятностей и математическая статистика.— M.: Высшая школа, 2003.

3. Пехлецкий И.Д. Математика. Учебник для СПО, 2-е изд. стереотип. – М.: Академия, 2002.

методические указания к решению первой

Контрольной работы

В этом параграфе приведён разбор решений задач типового варианта контрольной работы по математическому анализу.

ЗАДАЧА 1. Вычислить пределы функций а) —д):

а) 1. .

► = = .

2. .

► .= = = =0.◄

3. ..

► .= = = =-∞.

б) .

Решение. = = = =

= = =

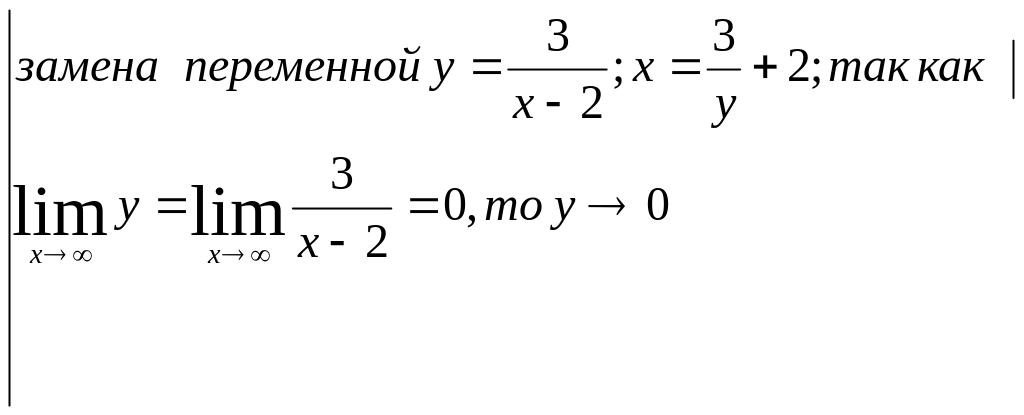
Предел вычислен подстановкой

П

редел не может быть вычислен подстановкой , поскольку в результате подстановки получается неопределенность .

в) .

Анализ задачи. Подстановка числа 2 вместо показывает, что пределы числителя и знаменателя равны нулю. Следовательно, нам потребуется раскрыть неопределенность . Для этого можно либо провести тождественные преобразования выражения , либо применить правило Лопиталя.

Решение. Выражение является сопряженным по отношению к выражению , а выражение - по отношению к . Умножая числитель и знаменатель дроби на произведение сопряженных выражений ( )·( ), и используя формулу разности квадратов , получаем

Другое решение задачи. Воспользуемся правилом Лопиталя

Ответ: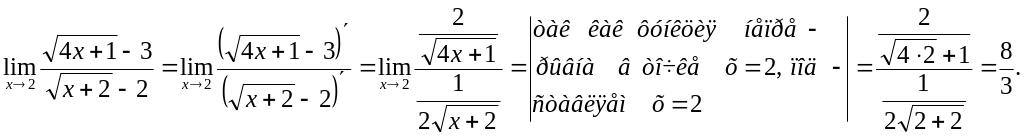

Анализ задачи. В данном случае, непосредственное применение те­оремы о пределе частного невозможного, поскольку, как показывает подстановка числа. -3 вместо x и предел числителя и предел знаме­натели равны пулю.

и

Таким образом, рассматриваемый предел представляет собой неопределённость вида и для решения задачи требуется про­вести тождественные преобразования выражения, находящего­ся под знаком предела.

Решение. Разложим числитель и знаменатель на множители, пользуясь следующей теоремой: если — корни квадратного трехчлена , то ,

= Решаем квадратное уравнение, находя его дискриминант D.

Отсюда,

Аналогично,

Поэтому,

Преобразуем выражение находящиеся под знаком предела:

= =

=

Другое решение задачи. Поскольку пределы числителя и знаменателя при

Равны нулю, применимо правило Лопиталя.

Ответ:10.

д)

Анализ задачи. Подстановка числа 0 вместо x показывает, что пределы числителя и знаменателя при равны нулю. Поэтому, имеет место неопределённость .

Для того, чтобы раскрыть неопределённость можно либо провести тождественные преобразования выражения, либо применить правило Лопиталя.

Решение. Совершим замену неизвестной при этом

Так как при то

Используем теперь тригонометрическую формулу