2.1.3 Алгоритм Дейкстри
Дан орієнтований або неорієнтований зважений граф з n вершинами і m ребрами. Ваги всіх ребер ненегативні. Вказана певна стартова вершина s. Потрібно знайти довжини найкоротших шляхів з вершини s у всі інші вершини, а також надати спосіб виведення самих найкоротших шляхів.
Ця задача називається "завданням про найкоротших шляхах з єдиним джерелом" (single-source shortest paths problem) [9].
Алгоритм запропонував голландський дослідник Дейкстра (Dijkstra) в 1959 р.
Заведемо масив d[], в якому для кожної вершини v будемо зберігати поточну довжину d[v] найкоротшого шляху з s в v. Спочатку d[s] = 0, а для всіх інших вершин ця довжина дорівнює нескінченності (при реалізації на комп'ютері зазвичай в якості нескінченності вибирають просто достатньо велике число, завідомо більшу можливої довжини шляху): d [v] = ∞, v ≠ s.
Крім того, для кожної вершини v будемо зберігати, позначена вона ще чи ні, тобто заведемо булевський масив u []. Спочатку всі вершини не помічені, тобто u[v] = {false}
Сам алгоритм Дейкстри складається з n ітерацій. На черговій ітерації вибирається вершина v з найменшою величиною d[v] серед ще не помічених (зрозуміло, що на першій ітерації вибрана буде стартова вершина s.):
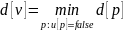(2.2)
Обрана таким чином вершина v відзначається поміченої. Далі, на поточній ітерації, з вершини v виробляються релаксації: проглядаються всі ребра (v, to), що виходять з вершини v, і для кожної такої вершини to алгоритм намагається поліпшити значення d[to]. Нехай довжина поточного ребра дорівнює len, тоді у вигляді коду релаксація виглядає як:
d[to] = min (d [to], d [v] + len).............................................(2.3)
На цьому поточна ітерація закінчується, алгоритм переходить до наступної ітерації (знову вибирається вершина з найменшою величиною d, з неї виробляються релаксації, і т.д.). При цьому в кінці кінців, після n ітерацій, всі вершини графа стануть поміченими, і алгоритм свою роботу завершує. Стверджується, що знайдені значення d[v] і є шукані довжини найкоротших шляхів з s в v.
Варто зауважити, що, якщо не всі вершини графа досяжні з вершини s, то значення d[v] для них так і залишаться нескінченними. Зрозуміло, що кілька останніх ітерацій алгоритму будуть як раз вибирати ці вершини, але ніякої корисної роботи виробляти ці ітерації не будуть (оскільки нескінчена відстань не зможе прорелаксувати інші, навіть теж нескінченні відстані). Тому алгоритм можна відразу зупиняти, як тільки в якості обраної вершини береться вершина з нескінченним відстанню.
Зрозуміло, зазвичай потрібно знати не тільки довжини найкоротших шляхів, але й отримати самі шляхи. Покажемо, як зберегти інформацію, достатню для подальшого відновлення найкоротшого шляху з s до будь-якої вершини. Для цього достатньо так званого масиву предків: масиву p[], в якому для кожної вершини v зберігається номер вершини p[v], що є передостанньою в найкоротшому шляху до вершини v. Тут використовується той факт, що якщо ми візьмемо найкоротший шлях до якоїсь вершини v, а потім видалимо з цього шляху останню вершину, то вийде шлях, що закінчується деякої вершиною p[v], і цей шлях буде найкоротшим для вершини p[v] . Отже, якщо ми будемо володіти цим масивом предків, то найкоротший шлях можна буде відновити за нього, просто кожен раз беручи предка від поточної вершини, поки ми не прийдемо в стартову вершину s - так ми отримаємо шуканий найкоротший шлях, але записаний у зворотному порядку. Отже, найкоротший шлях P до вершини v дорівнює:
P = (s, ..., p [p [p [v]]], p [p [v]], p [v], v)..................................(2.4)
Залишилося зрозуміти, як будувати цей масив предків. Однак це робиться дуже просто: при кожній успішній релаксації, тобто коли з обраної вершини v відбувається поліпшення відстані до деякої вершини to, ми записуємо, що предком вершини to є вершина v: p[to] = v
Отже, алгоритм Дейкстри являє собою n ітерацій, на кожній з яких вибирається Непомічені вершина з найменшою величиною d [v], ця вершина позначається, і потім проглядаються всі ребра, що виходять з даної вершини, і вздовж кожного ребра робиться спроба поліпшити значення d [] на іншому кінці ребра.
Час роботи алгоритму складається з:
n разів пошук вершини з найменшою величиною d[v] серед усіх непозначених вершин, тобто серед O (n) вершин;
m раз проводиться спроба релаксацій.
При найпростішій реалізації цих операцій на пошук вершини буде витрачатися O(n) операцій, а на одну релаксацію - O(1) операцій, і підсумкова асимптотика алгоритму становить: O (n2 + m)
На розріджених графах, де кількість ребер не пропорціональна квадрату кількості вершин, використовуючи структури даних типу купи, можна добитися асимптотики О(m * log(n)).