2.1 Точні алгоритми

Точний алгоритм – це алгоритмічний процес, який видає унікальний і передбачений результат для заданих вхідних даних.

2.1.1 Пошук в ширину на незваженому графі.

Пошук в ширину (обхід в ширину, breadth-first search) - це один з основних алгоритмів на графах.

В результаті пошуку в ширину знаходиться шлях найкоротшої довжини в незваженим графі, тобто шлях, що містить найменше число ребер.

Алгоритм працює за O (n + m), де n - число вершин, m - число ребер.

На вхід алгоритму подається заданий граф (незважений), і номер стартовою вершини s. Граф може бути як орієнтованим, так і неорієнтованим, для алгоритму це не важливо.

Сам алгоритм можна розуміти як процес "підпалювання" графа: на нульовому кроці підпалюємо тільки вершину s. На кожному наступному кроці вогонь з кожною вже палаючої вершини перекидається на всіх її сусідів; тобто за одну ітерацію алгоритму відбувається розширення "кільця вогню" в ширину на одиницю (звідси і назва алгоритму).

Більш строго це можна представити таким чином. Створимо чергу Q, в яку будуть міститися палаючі вершини, а також заведемо булевий масив used[], в якому для кожної вершини будемо відзначати, горить вона вже чи ні (або іншими словами, чи була вона переглянуло).

Спочатку в чергу поміщається тільки стартова вершина s ( , де V - множина всіх вершин графу), та used[s] = true, а для всіх інших used[] = false. Потім алгоритм являє собою цикл: поки черга не порожня, дістати з її голови одну вершину, переглянути всі ребра, що виходять з цієї вершини, і якщо якісь з переглянутих вершин ще не горять, то підпалити їх і помістити в кінець черги.

У підсумку, коли черга спорожніє, обхід в ширину обійде всі досяжні з s вершини, причому до кожної дійде найкоротшим шляхом. Також можна порахувати довжини найкоротших шляхів (для чого просто треба завести масив довжин шляхів distance[]), і компактно зберегти інформацію, достатню для відновлення всіх цих найкоротших шляхів (для цього треба завести масив "предків" parent[], в якому для кожної вершини зберігати номер вершини, по якій ми потрапили в цю вершину).

Основним недоліком даного алгоритму є те, що він не працює для зважених графів у загальному випадку, тому його використання у нашому проекті, де окрім сусідніх вершин з відстанню рівною 1 є вершини з відстанню, яка рівна (точки на карті, які з'єднані діагоналлю), є нераціональним.

2.1.2 Алгоритм Флойда-Уоршелла

Даний алгоритм представляє собою простий метод пошуку найкоротших відстаней між усіма точками (вершинами) на графі.

Для цього алгоритму вхідними даними виступає орієнтований або неорієнтований зважений граф G з n вершинами. Потрібно знайти значення всіх величин - довжину найкоротшого шляху з вершини u в вершину v.

Передбачається, що граф не містить циклів негативної ваги (тоді відповіді між деякими парами вершин може просто не існувати - він буде нескінченно маленьким).

Цей алгоритм був одночасно опубліковано в статтях Роберта Флойда (Robert Floyd) [7] і Стівена Уоршелла (Stephen Warshall) [8] в 1962 р., на ім'я яких цей алгоритм і називається в даний час. Ключова ідея алгоритму - розбивка процесу пошуку найкоротших шляхів на фази.

Перед k-ой фазою (k = 1...n) вважається, що в матриці відстаней distance збережені довжини таких найкоротших шляхів, які містять в якості внутрішніх вершин тільки вершини з множини {1, 2, ..., k-1}.

Іншими словами, перед k-ою фазою величина дорівнює довжині найкоротшого шляху з вершини u в вершину v, якщо цьому шляху дозволяється заходити тільки в вершини з номерами, меншими k (початок і кінець шляху не вважаються).

Легко переконатися, що щоб ця властивість виконалось для першої фази, достатньо в матрицю відстаней записати матрицю суміжності графа: = 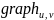- вартості ребра з вершини u в вершину v. При цьому, якщо між якимись вершинами ребра немає, то записати слід величину "нескінченність". З вершини в саму себе завжди слід записувати величину 0, це критично для алгоритму.

Нехай тепер ми перебуваємо на k-ій фазі, і хочемо перерахувати матрицю distance таким чином, щоб вона відповідала вимогам вже для k+1-ї фази. Зафіксуємо якісь вершини u та v. У нас виникає два принципово різних випадки:

1. найкоротший шлях з вершини u в вершину v, якому дозволено додатково проходити через вершини {1, 2, .., k}, збігається з найкоротшим шляхом, якому дозволено проходити через вершини множини {1, 2, ..., k-1}. У цьому випадку величина не зміниться при переході з k-ї на k+1-у фазу;

2. "новий" найкоротший шлях став краще "старого" шляху. Це означає, що "новий" найкоротший шлях проходить через вершину k. Відразу відзначимо, що ми не втратимо спільності, розглядаючи далі тільки прості шляхи (тобто шляху, не проходять по якійсь вершині двічі). Тоді зауважимо, що якщо ми розіб'ємо цей "новий" шлях вершиною k на дві половинки (одна йде u → k, а інша - k → v), то кожна з цих половинок уже не заходить у вершину k. Але тоді виходить, що довжина кожної з цих половинок була порахована ще на k-1-й фазі або ще раніше, і нам достатньо взяти просто суму , вона й дасть довжину "нового" найкоротшого шляху.

Об'єднуючи ці два випадки, отримуємо, що на k-й фазі потрібно перерахувати довжини найкоротших шляхів між всіма парами вершин u та v таким способом:

(2.1)

Таким чином, вся робота, яку потрібно провести на k-й фазі - це перебрати всі пари вершин і перерахувати довжину найкоротшого шляху між ними. В результаті після виконання n-ої фази в матриці відстаней буде записана довжина найкоротшого шляху між u та v, або "безмежність", якщо шляхи між цими вершинами не існує.

Асимптотика алгоритму, очевидно, становить O (n³).