4. Линейные уравнения высших порядков

4.1. Решить задачу Коши:

(a)

Решение. Находим общее решение однородного дифференциального уравнения (дифура), соответствующего исходному дифуру (а):

(b)

Его характеристическое уравнение а корни Тогда общее решение дифура (b) будет:

(с)

Частное решение исходного дифура (а) берем в виде:

(d)

тогда

,

подставляем в (а) и группируем: , отсюда, приравняв коэффициенты при одинаковых степенях х, имеем:

и ,

т.е. , а выражение (d) принимает вид:

(е)

Суммируя (с) и (е), найдем общее решение неоднородного диф. уравнения (а):

(f)

Найдем и, используя начальные условия (а), имеем:

отсюда

Найденные значения С₁ и С₂ подставляем в (f), и тогда частное решение исходного дифференциального уравнения имеет вид:

4.2. Решить задачу Коши:

(а)

Решение. Однородное дифуравнение

(b)

имеет характеристическое уравнение , а его корни будут . Тогда общее решение дифура (b) будет:

(с)

Частное решение дифура (а) ищем в виде:

(d)

Определив и и подставив в (а), после группировки имеем

отсюда или и Подставляя А и В в (d) и суммируя с (с), найдем общее решение дифура (а):

(е)

Найдем и, используя начальные условия (а), имеем

отсюда

Подставляя найденные С₁ и С₂ в (е), будем иметь решение исходного дифференциального уравнения (а), удовлетворяющего начальным условиям:

5. Двойной интеграл

5.1. Изобразить и найти площадь фигуры, ограниченной линиями:

и .

Решение. Построим две параболы и найдем точки пересечения:

отсюда или , его корни x₁ = 4, x₂ = 12. На чертеже (рис. 2) изображена заштрихованная фигура, площадь которой определяем:

(кв. ед.)

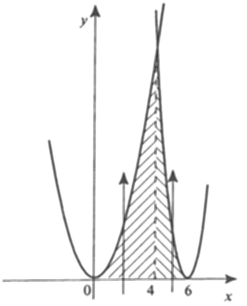
Рис. 2

6. Числовые ряды

6.1. Исследовать на сходимость ряды с положительными членами:

Решение. Имеем

Исследуем сходимость ряда по признаку Даламбера:

Следовательно, ряд расходится.

7. Степенные ряды

7.1. Найти область сходимости степенного ряда:

Решение. Согласно признаку Даламбера искомый ряд сходится при тех значениях х, для которых:

т.е.

Исследуем сходимость ряда на концах интервала.

При получаем числовой ряд

Это знакочередующийся ряд, для которого

т.е. по признаку Лейбница ряд расходится.

При имеем числовой ряд с положительными членами

который расходится, так как предел общего числа не равен нулю.

Итак, область сходимости данного ряда

Задания контрольной работы

1. Найти частные производные функций:

а) ;

б) .

2. Найти дифференциал функции

3. Составить уравнение касательной плоскости и нормали к поверхности в точке .

4. Для функции в точке найти градиент и производную по направлению .

5. Найти наибольшее и наименьшее значения функции в области, заданной неравенствами:

6. Найти общее решение уравнения

7. Скорость роста банковского вклада пропорциональна величине вклада. Коэффициент пропорциональности равен m. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла n миллионов рублей.

8. Решить задачу Коши: .

9. Решить задачу Коши: .

10. Изобразить и найти площадь фигуры, ограниченной линиями:

и .

11. Исследовать на сходимость ряд с положительными членами .

12. Найти область сходимости степенного ряда