Система со скользящим резервом

Р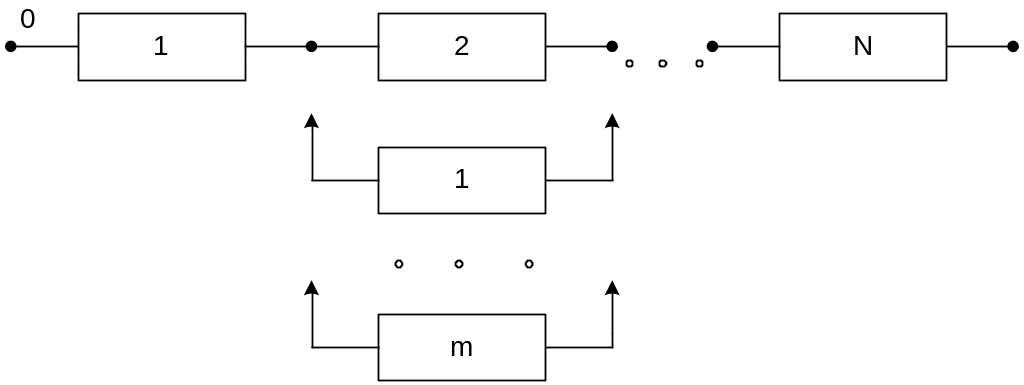 ассмотрим систему со скользящим резервом, у которой основная подсистема содержит N последовательно соединенных одинаковых элементов и m аналогичных резервных элементов. Переключатель при отказе любого из основных элементов подключает вместо него очередной резервный элемент. Резервированная система будет работоспособной до тех пор, пока не произойдет m+1 отказов.

Считаем, что поток отказов простейший; все элементы, находящиеся в работе, равнонадежны; резервные элементы до момента замещения не нагружены, то есть отказать не могут; отказавшие элементы в процессе работы системы не восстанавливаются; переключатели абсолютно надежные. Определим показатели надежности.

Так как система является работоспособной до (m+1) отказа, то вероятность безотказной работы системы со скользящим резервом за наработку t

(1),

где Р(Н_j) – вероятность того, что система находится в благоприятном состоянии к моменту времени t, при котором отказали ровно j элементов;

Так как поток отказов простейший, то имеет место экспоненциальный закон надежности, а величина j подчинена закону Пуассона, то есть Р(Н_j):

(2)

Р_j(t) – вероятность того, что за время t отказало ровно j элементов;

- интенсивность отказов основной подсистемы.

,

где - интенсивность отказов одного элемента, тогда (2) в (1), получим

(3)

Средняя наработка до отказа

(4)

Сравним полученные результаты, то есть соотношения (3) и (4) соответственно с выражениями (4) и (5) для системы с общим ненагруженным резервом. Сравнение показывает, что эти выражения совпадают, то есть показатели надежности и выигрыш в надежности одинаковый для рассматриваемых случаев. Однако при скользящем резервировании требуется в N раз меньше резервных элементов, что дает значительную экономию по массе, габаритным характеристикам и стоимости системы. Таким образом, скользящее резервирование с ненагруженным резервом является наиболее эффективным (при одинаковой избыточности) при условии, что переключатели абсолютно надежны. При ненадежном переключателе, чтобы повысить надежность системы необходимо использовать высоконадежный переключатель.

1.4 Учет вида отказов в системе с резервом

Элемент может отказать из-за обрыва или из-за короткого замыкания. Оценим показатели надежности системы с резервом с учетом видов отказов.

Считаем, что отказы, вызванные обрывом или коротким замыканием независимы; элементы равнонадежные, то есть используется нагруженное резервирование; переключатели абсолютно надежные и отказавшие элементы в процессе работы системы не восстанавливаются.

Пусть P₀(t) и Р_з(t) – вероятности безотказной работы элемента соответственно на обрыв и короткое замыкание за наработку t. Считаем, что

- интенсивности отказов элемента соответственно на обрыв и короткое замыкание.

Элемент, у которого два вида отказов можно представить в виде двух последовательно соединенных эквивалентных элементов, один из которых отказывает только из-за обрыва, а другой – только из-за к.з.

Вероятность безотказной работы такого элемента

Средняя наработка до отказа элемента с отказами двух видов:

Если элемент с двумя видами отказов зарезервировать с кратностью m, то есть используется общий нагруженный резерв, то схему расчета надежности можно представить исходя из следующего соображения: система откажет, если произойдет обрыв совместно в m+1 элементах или произойдет отказ из-за короткого замыкания хотя бы в одном элементе.

С учетом принятых допущений вероятность безотказной работы резервированной системы за наработку t

(*)

(1)

Средняя наработка до отказа

(2)

Из соотношений (1) и (2) следует, что надежность системы с ростом кратности резервирования m увеличивается по отказам из-за обрывов и уменьшается по отказам из-за короткого замыкания.

Рассмотрим простейший случай, когда m=1 (дублирование). Согласно (*), вероятность безотказной работы такой системы

Чтобы у рассматриваемой системы был выигрыш в надежности по вероятности безотказной работы необходимо, чтобы

>1

Средняя наработка до отказа этой системы с учетом (2)

Выигрыш надежности по Т_ср. для рассматриваемого случая будет иметь место, если сомножитель

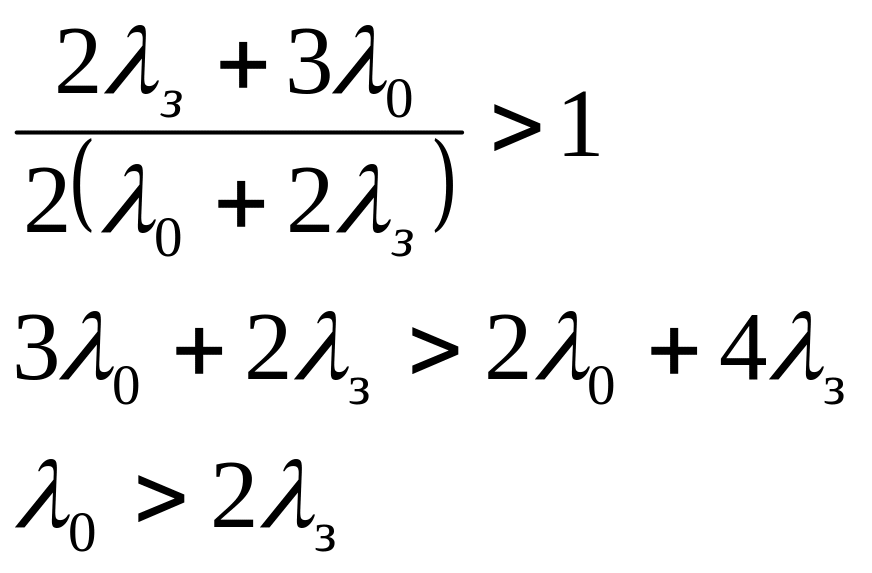
Получили условия для m=1. Рассмотрим другие случаи m=2,3,… и находя условия для них, применив метод математической индукции, можно прийти к следующему заключению: интенсивность отказов

Таким образом, из-за к.з. элементов значительно уменьшается надежность и следовательно эффективность резервирования. Чтобы устранить влияние к.з. последовательно с элементами подключают предохранители, которые срабатывают в момент к.з., разрывая цепь элементов. Это приводит к тому, что вместо отказа из-за к.з. возникает отказ типа «обрыв», тогда элемент системы с предохранителем представляется в виде последовательного соединения двух эквивалентных элементов Р₀(t) и Р_з(t) и предохранителя Р_пр(t), а резервированная система, как система с общим нагруженным резервом. Тогда вероятность безотказной работы рассматриваемой системы за наработку t

Средняя наработка до отказа системы с нагруженным резервом, элементы которой отказывают из-за обрыва, короткого замыкания и подключены к предохранителю

Из соотношений (3), (5) видно, что с увеличением кратности резервирования m надежность системы увеличивается, то есть введение предохранителей увеличивает надежность системы, в которой элементы могут отказать из-за к.з.

Пример 2:

Основная подсистема резервированной системы содержит два последовательно соединенных элемента (N = 2). Элементы равнонадежны с

Задана наработка t = 5 ч. Рассматриваемая система дублированная (m=1). Оценить вероятность безотказной работы резервированной системы за заданную наработку, среднюю наработку до отказа, выигрыш в надежности по вероятности отказа и выигрыш в надежности по средней наработке до отказа для следующих случаев:

а) с общим нагруженным резервом

б) с раздельным нагруженным резервом

в) с общим ненагруженным резервом

г) с раздельным ненагруженным резервом

д) со скользящим резервом

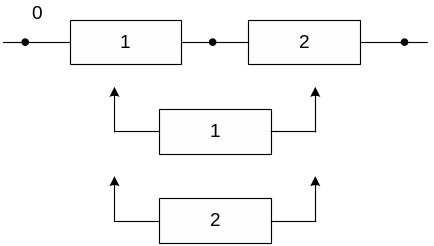
Решение:

а)