Надежность систем с раздельным резервом

В многоэлементных системах широко используется раздельное (поэлементное) резервирование. В этом случае резервными элементами являются радиоэлектронные элементы, блоки, устройства, ЭВМ, комплексы, подсистемы.

Система с раздельным резервом

Пусть основная подсистема состоит из N последовательно соединенных элементов, каждый из которых резервируется m аналогичными элементами. Покажем это на следующем рисунке:

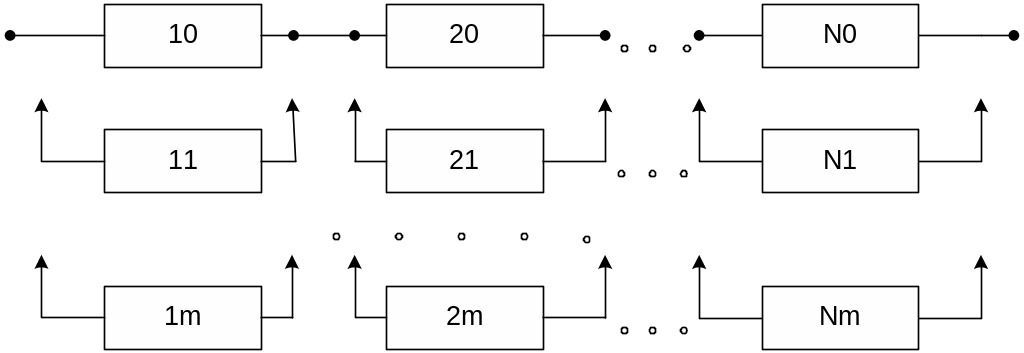
Примем следующие допущения.

Считаем, что поток отказов простейший, отказавшие элементы в процессе работы системы не восстанавливаются, переключатели абсолютно надежны.

Так как элемент i-го типа резервируется m аналогичными элементами, то вероятность безотказной работы i-ой группы элементов Р_{i гр}(t). Группы элементов соединены последовательно, поэтому вероятность безотказной работы системы с раздельным резервом за наработку t

(*)

Формула(*) дает общий вид для вероятности безотказной работы рассматриваемой системы. Очевидно, что величину P_i.гр(t) можно определить по соотношениям, полученным для системы с общим резервом.

а) Система с нагруженным резервом

Согласно соотношению (4) (смотри соответствующую лекцию по нагруженному резервированию) с равнонадежными элементами i-го типа по формуле (*) получим:

Согласно принятому допущению имеет место экспоненциальный закон надежности элементов системы, то есть

- это интенсивность отказов i-го элемента. Тогда

Средняя наработка до отказа

б) Система с облегченным резервом.

Согласно выражению (4) при облегченном резерве (смотри соответствующую лекцию) по формуле (*) получим

(**)

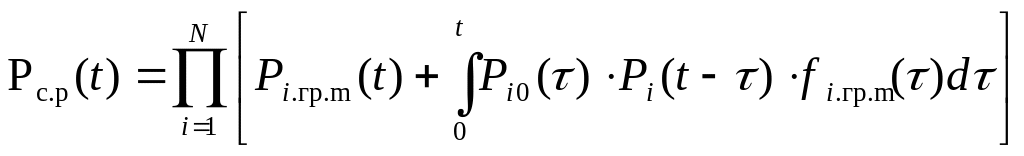
где Р_i.гр.m(t) – вероятность безотказной работы i-ой группы элементов с кратностью m-1 за наработку t ;

- вероятность работоспособного состояния i-го резервного элемента к моменту замещения;

- плотность вероятности отказа i-ой группы элементов с кратностью резервирования m-1 .

При экспоненциальном законе надежности элементов вероятность безотказной работы системы с раздельным облегченным резервом за наработку t согласно формулам (**) и (5) при облегченном резерве (смотри соответствующую лекцию) примет вид

где коэффициент

;

- интенсивность отказов работающего элемента i-ой группы;

- интенсивность отказов резервного элемента i-ой группы до момента замещения.

Средняя наработка до отказа рассматриваемой системы определяется по аналогии с нагруженным резервированием.

в) Система с ненагруженным резервированием.

Согласно соотношению (3) при ненагруженном резервировании (смотри соответствующую лекцию) по формуле (*) в окончательном виде получим

(***),

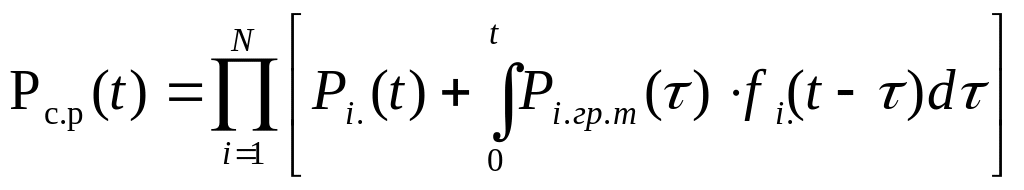
где - плотность вероятности отказа элемента i-го типа

При экспоненциальном законе надежности элементов вероятность безотказной работы системы с раздельным ненагруженным резервом за наработку t согласно формулам (***) и (4) имеет следующий вид:

Средняя наработка до отказа определяется аналогично случаю с нагруженным резервированием.

Сравнивая полученные результаты для вероятности безотказной работы за наработку t системы с раздельным резервом с соответствующими выражениями для системы с общим резервом, приходим к следующему выводу: при прочих одинаковых условиях раздельное резервирование более эффективно по сравнению с общим при условии, что переключатели абсолютно надежные. Однако при раздельном резервировании требуется в N раз больше переключателей, чем при общем резервировании. Чтобы получить наибольший выигрыш в надежности при раздельном резервировании, необходимо обеспечить систему высоконадежными переключателями.