Система с дробной кратностью резервирования

N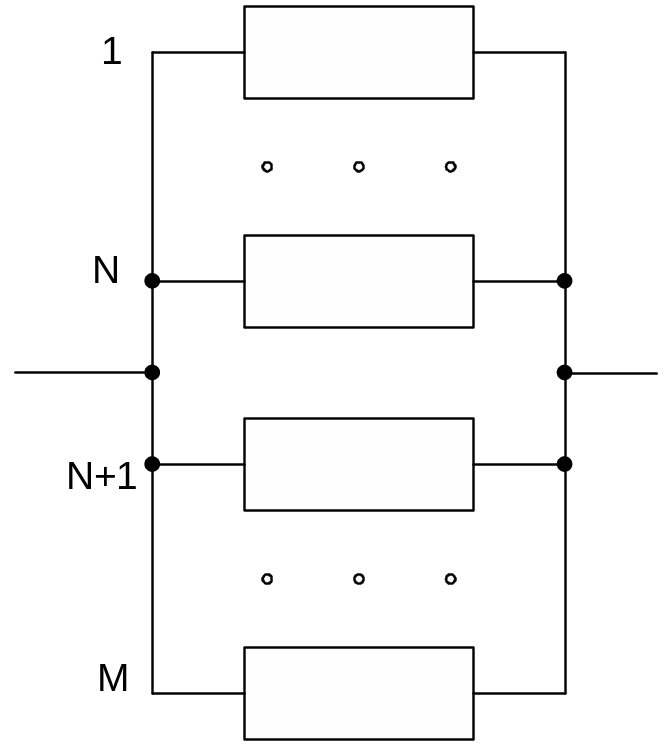 – число основных подсистем параллельно соединенных между собой;

M-N – число резервных нагруженных подсистем

Кратность резервирования:

Система является работоспособной, если не отказало более M-N подсистем. Простейшим примером такой подсистемы является параллельное включение двух источников питания, которые удовлетворяют требованию по мощности. Эти источники питания будут основными. К ним параллельно подключен резервный источник питания. В этом случае m=1/2. Необходимо определить показатели надежности системы с дробной кратностью резервирования. Для решения сделаем следующие допущения. Считаем, что все подсистемы равнонадежны; поток отказов простейший; все переключатели абсолютно надежные; отказ подсистемы в процессе работы не восстанавливается. Вероятность безотказной работы Р_с(t). Число благоприятных состояний, которые определяют работоспособность системы . Так как рассматриваемое состояние представляет собой несовместимые события, то вероятность безотказной работы системы с дробной кратностью резервирования:

(1),

где Р(Н_j) – вероятность того, что система находится в благоприятном состоянии H_j, в котором имеет место ровно j отказавших подсистем. При этом величина и . С учетом принятого допущения

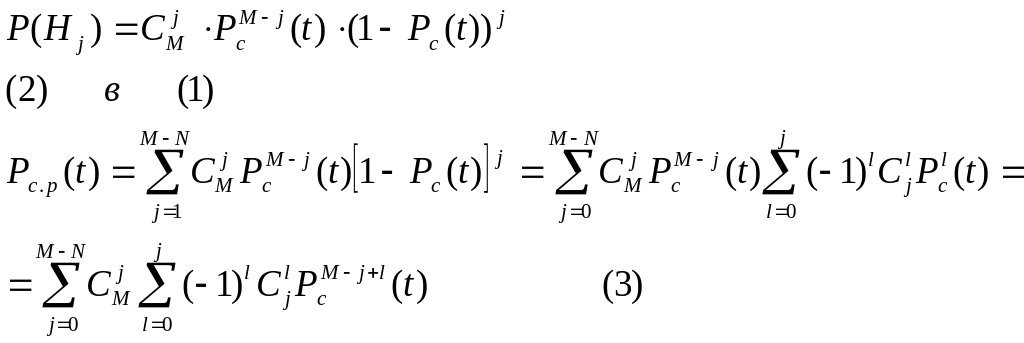
Так как поток отказов простейший, то есть интенсивность отказов

Тогда (3) принимает вид

О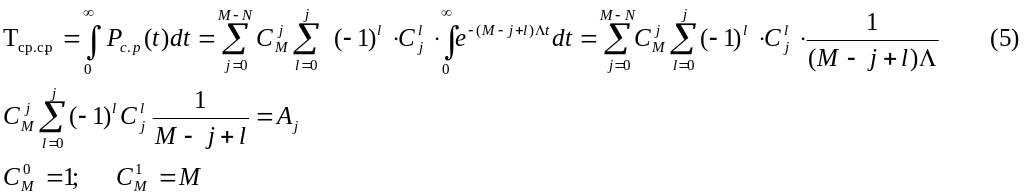 пределим среднюю наработку до отказа рассматриваемой системы

Рассмотрим j=0:

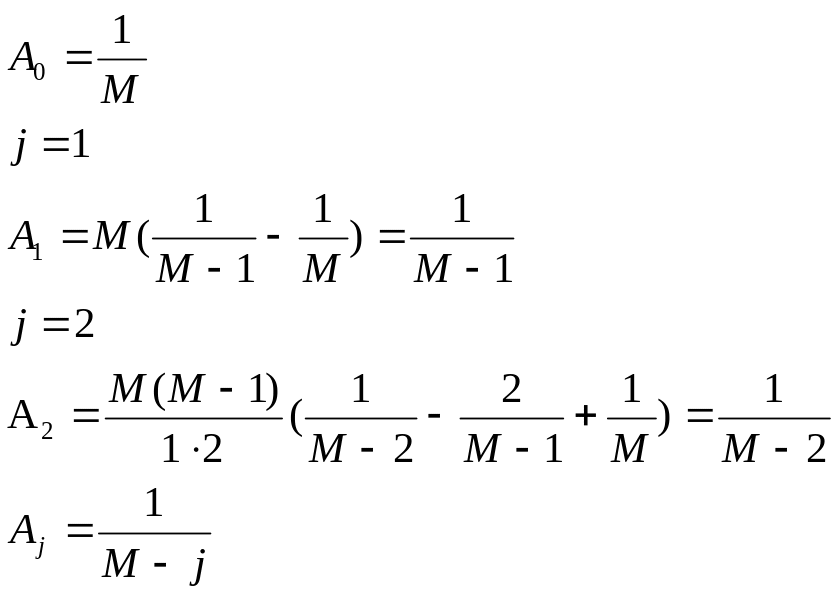
Средняя наработка до отказа

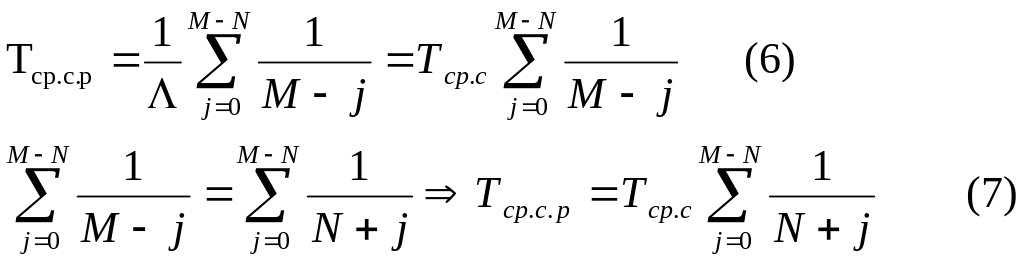
Сравним средние наработки до отказа системы с другой кратностью резервирования и аналогичные системы с целой кратностью резервирования, то есть m=М-1

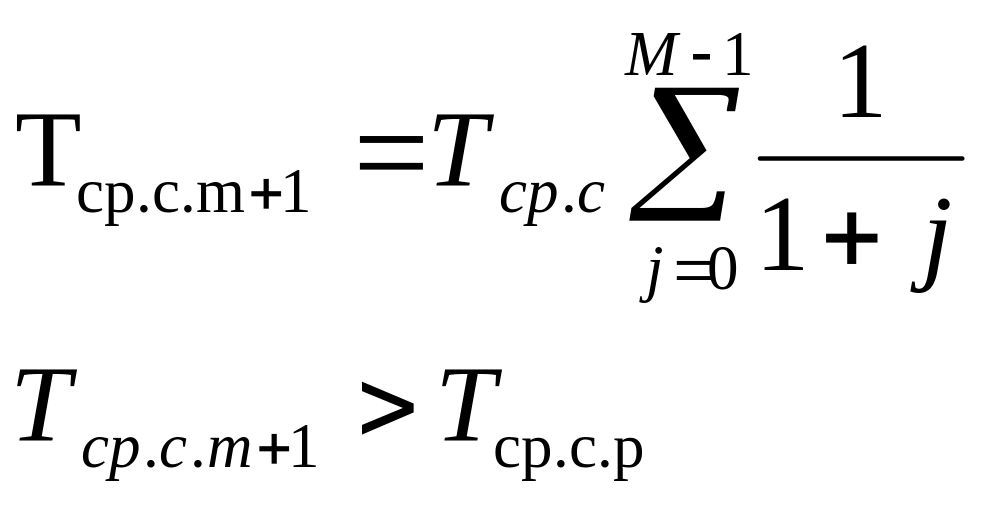
Решение:

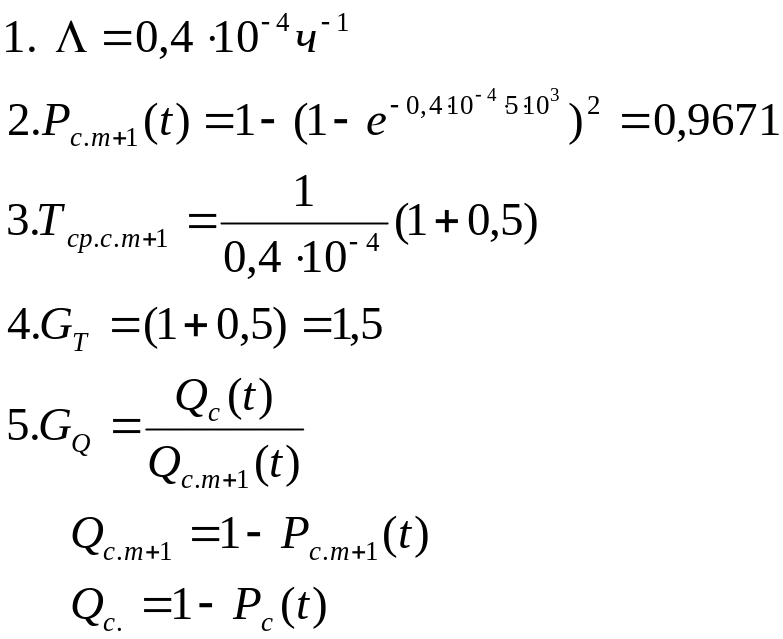
Мажоритарное резервирование

Мажоритарное резервирование – частный случай резервирования с дробной кратностью, когда резервных подсистем на одну меньше, чем основных, то есть

M – N = N – 1

Мажоритарное резервирование также называют резервированием по принципу «голосования по большинству», так как система имеет восстанавливающий элемент, который выдает правильные данные, которые получены от большинства работоспособных подсистем. Рассмотрим наиболее простую и часто применяемую схему системы с мажоритарным резервированием.

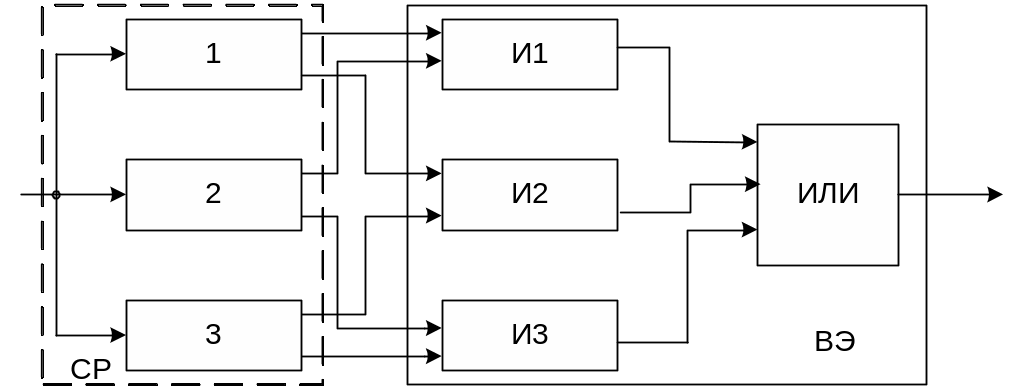
Резервированная система СР состоит из трех подсистем (М=3, N=2). Восстанавливающий элемент ВЭ состоит из трех элементов И и одного ИЛИ.

Данная схема широко используется в системах передачи и обработки дискретной информации, работающих в условиях помех, когда предъявляются повышенные требования к надежности аппаратуры и достоверности информации. Результат обработки информации считается правильным, если совпали результаты не менее двух ЭВМ. Примем следующие допущения: все подсистемы равнонадежные, восстанавливающий элемент абсолютно надежный, поток отказов простейший, при отказе подсистемы она не восстанавливается в процессе работы. Вероятность безотказной работы каждой подсистемы за наработку t - Р_с(t). Необходимо определить показатели надежности рассматриваемой системы. Для оценки вероятности безотказной работы системы с мажоритарным резервированием используем соответствующее выражение для системы с дробной кратностью резервирования

(1)

Для нашего случая

(2)

Так как поток отказов простейший, то есть

,

то имеет место экспоненциальный закон надежности и поэтому

(3)

Оценим среднюю наработку системы до отказа

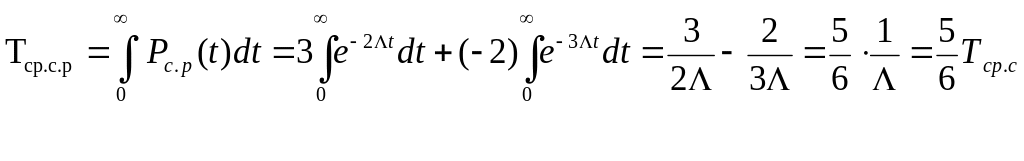
(4)

Оценим выигрыш в надежности по средней наработке до отказа рассматриваемой системы

Таким образом, по сравнению с одной подсистемой резервированная система дает проигрыш в надежности по средней наработке до отказа. Это связано с тем, что для безотказной работы системы необходима совместная работа не менее двух подсистем. Оценим выигрыш в надежности по вероятности Р(t) рассматриваемой системы

Чтобы выигрыш G_P имел место необходимо

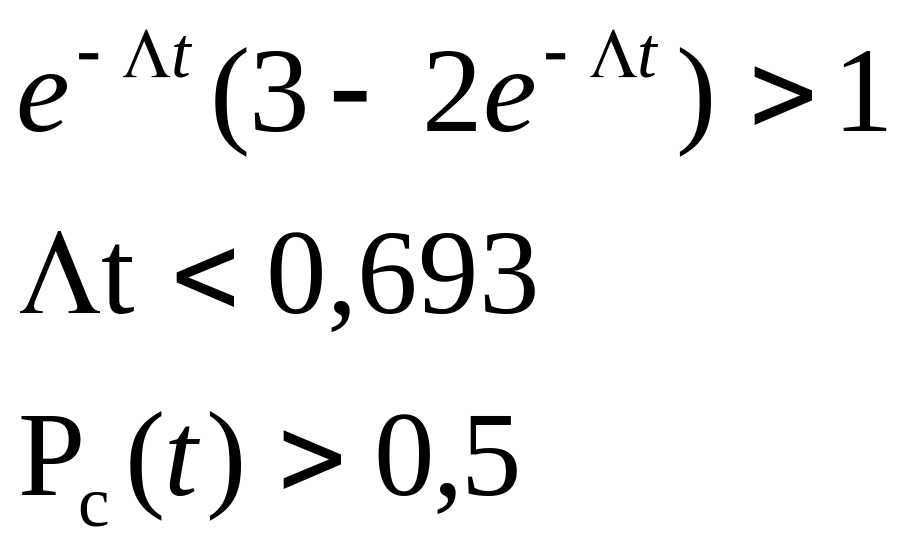
Из рисунка следует, что при

Рассмотрим случай с ненадежным ВЭ. Все элементы И являются равнонадежными, вероятность безотказной работы элементов И – Р_И(t), ИЛИ – P_ИЛИ(t). Так как поток отказов простейший, то используя метод перебора благоприятных гипотез в окончательном виде получим

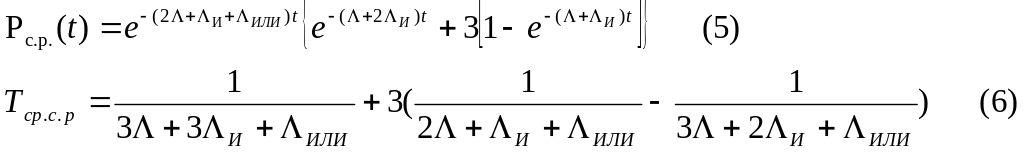
Таким образом, из (5) и (6) следует,что показатели надежности системы с мажоритарным резервированием уменьшаются с увеличением интенсивности отказов ВЭ.