Система с ненагруженным резервом

Ненагруженный резерв применяется в системах с резервированием замещением, в которых допускается перерыв в работе на время переключения подсистем и вхождения резервной подсистемы в рабочий режим работы. Так как резервные подсистемы при ненагруженном резервировании обесточены, то считают, что они до момента замещения отказать не могут. Считают, что резервная подсистема при замещении скачком переходит в рабочий режим работы (очевидно интенсивность отказов тоже изменяется скачком).

В остальном постановка задачи аналогична постановке для системы с облегченным резервом.

Необходимо определить показатели надежности системы с m-кратным ненагруженным резервом.

Так как ненагруженный резерв является частным случаем облегченного резерва, то для оценки вероятности безотказной работы рассматриваемой системы за время t воспользуемся соотношением (4) из предыдущей лекции.

(1)

С учетом того, что для системы с ненагруженным резервом вероятность работоспособного состояния резервной подсистемы к моменту Р_с.0( ) = 1, тогда

(2)

Произведем замену в выражении (2) с учетом того, что f_c.m.( )d =dQ_c.m( ), где Q_c.m( ) – вероятность отказа системы с кратностью резервирования m-1 за наработку .

(3)

Если закон надежности для работающих подсистем экспоненциальный, т.е.

Рассмотрим простейший случай – дублирование (m = 1)

Подставим в (3):

В общем случае для m 1 вероятность безотказной работы системы с m-кратным ненагруженным резервом за заданную наработку t:

(4)

Средняя наработка до отказа рассматриваемой системы

(5)

Оценим выигрыш в надежности по средней наработке до отказа.

Если сравнить выигрыш в надежности G_T для трех видов систем с общим резервом, то несложно заметить, что наиболее эффективным является ненагруженное резервирование при условии, что переключатели абсолютно надежные.

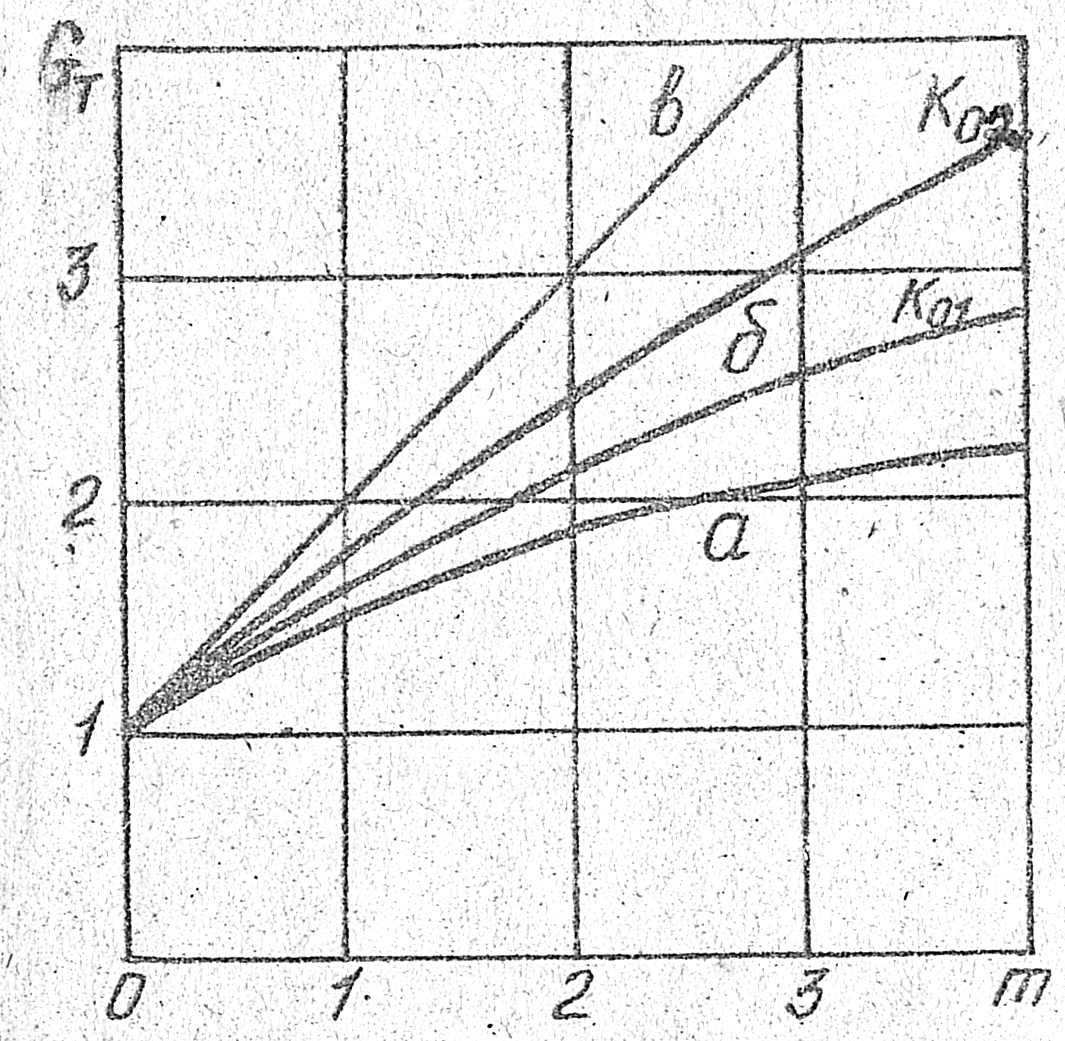
а) система с нагруженным резервом;

б) система с облегченным резервом ( K₀₁ >K₀₂ );

в) система с ненагруженным резервом.

Учет надежности переключателей в системе с резервом

Оценим влияние надежности переключателей на показатели надежности резервированной системы.

1. Переключатель общий

П ереключатель соединен последовательно с с.р., то есть отказ его приводит к отказу всей системы. Тогда, вероятность безотказной работы системы с m-кратным резервом и общим переключателем за наработку t:

(1)

где P_c.m+1(t) – вероятность безотказной работы системы с m-кратным резервом.

P_П(t) – вероятность безотказной работы переключателя за наработку t.

а) Рассмотрим систему с нагруженным резервом

,

где Р_с(t) – вероятность безотказной работы одной подсистемы за наработку t.

,

где Р_i(t) – вероятность безотказной работы i-го элемента.

N – число последовательно соединенных элементов.

Считаем, что интенсивность отказов подсистемы

и интенсивность отказов переключателя

Тогда

(2)

Оценим среднюю наработку до отказа системы

( 3),

где - средняя наработка до отказа одной подсистемы;

- коэффициент надежности переключателя.

б) Система с облегченным резервом

,

где - интенсивность отказов резервной подсистемы до момента

О ценим среднюю наработку до отказа

(5)

в) Система с ненагруженным резервом

(6),

(7)

Таким образом, из полученных соотношений (2) – (7) следует, что показатели надежности резервированной системы Р_с.(m+1)п(t) и Т_{ср.с.(m+1)п} ,а также их выигрыш уменьшаются с увеличением коэффициента К_п. Из (3) и (7) следует, что для дублированной системы (m = 1) с ненадежным переключателем может быть получен проигрыш в надежности по средней наработке до отказа; в случае нагруженного резерва при К_П>0,4142; для ненагруженного – при К_П>0, 618

2. Переключатели индивидуальные

К аждая из подсистем имеет индивидуальный переключатель, отказ которого приводит к отказу подсистемы, то есть вероятность безотказной работы работающей подсистемы

Р_с.п(t)=Р_с(t)Р_п(t) (8)

Для экспоненциального закона надежности элементов

отсюда следует

а) Система с нагруженным резервом

Вероятность безотказной работы системы с m-кратным нагруженным резервом и индивидуальными переключателями

С учетом экспоненциального закона надежности элементов вероятность безотказной работы:

Средняя наработка до отказа рассматриваемой системы

(10)

б) Система с облегченным резервом

Вероятность безотказной работы системы с m-кратным облегченным резервом с индивидуальными переключателями получается аналогично случаю с абсолютно надежными переключателями. С учетом того, что имеет место экспоненциальный закон надежности элементов, в окончательном виде можно записать

(11),

где - средняя наработка до отказа рассматриваемой системы.

( 12)

в) Система с ненагруженным резервом

Вероятность безотказной работы системы с m-кратным ненагруженным резервом с индивидуальными переключателями за наработку t получается аналогично случаю с облегченным резервом с абсолютно надежными переключателями. С учетом экспоненциального закона надежности элементов получим:

(13),

где

С редняя наработка системы до отказа

(14)

В соответствии (10) и (14) проигрыш в надежности может быть получен в дублированных системах (m = 1) с индивидуальными переключателями, если К_П>0,5 при нагруженном резерве и К_П>0,7071 при ненагруженном резерве. Из полученных соотношений следует, что для повышения надежности систем с резервом необходимо стремиться уменьшить значение К_П или увеличить надежность переключателей.