
- •Конспект лекций по дисциплине «Современные методы технического обслуживания»
- •220500 «Управление качеством»
- •Литература
- •Основные понятия резервирования
- •Надежность систем с общим резервом Система с постоянно включенным нагруженным резервом
- •Система с облегченным резервом
- •Система с ненагруженным резервом
- •Система с дробной кратностью резервирования
- •Мажоритарное резервирование
- •Надежность систем с раздельным резервом
- •Система с раздельным резервом
- •Система со скользящим резервом
- •1.4 Учет вида отказов в системе с резервом
- •1.5 Оптимизация надежности системы с раздельным резервом методом Лагранжа
- •1.6 Надежность восстанавливаемых резервированных систем Резервированная восстанавливаемая система как система массового обслуживания
- •1.6.2 Резервированная восстанавливаемая система с поглощающим экраном
- •1.6.3 Резервированная восстанавливаемая система с отражающим экраном
- •2.2 Контроль технического состояния объектов в процессе их эксплуатации
- •2.2.1 Проблемы профилактического обслуживания
- •2.2.2 Профилактическое обеспечение сложных систем
- •2.2.3 Уменьшение времени восстановления при текущем ремонте аппаратуры
- •2.2.4 Система планово – предупреждающего ремонта энергетического оборудования
- •2.2.5 Расчет числа запасных изделий. Исходные положения
- •2.2.6 Расчет числа запасных изделий для случая, когда отказавшие элементы не восстанавливаются
- •2.2.7 Расчет числа запасных изделий для случая, когда отказавшие элементы восстанавливаются
- •Основное изделие (объект)
- •Ремонтный орган
Система с облегченным резервом
Система с облегченным резервом применяется в случаях резервирования с замещением, т.е. когда функции основного элемента передаются резервному только после отказа основного элемента. В этих системах допускаются кратковременные перерывы в работе для переключения подсистем после их отказа (в моменты отказов)
Рассмотрим систему с облегченным m-кратным резервом. В ней основные и резервные подсистемы состоят из N последовательно соединенных элементов. представим эту систему в виде элементов расчета надежности.
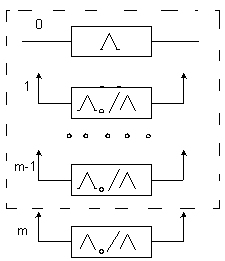
![]() -
интенсивность отказов основной
подсистемы;
-
интенсивность отказов основной
подсистемы;
0 – интенсивность отказа резервных подсистем.
Необходимо определить показатели надежности системы с облегченным m-кратным резервом.
Для
определения показателей надежности
сделаем следующие допущения: считаем,
что в процессе работы отказавшие
подсистемы не восстанавливаются,
переключатели абсолютно надежные; все
подсистемы одинаковые;
резервные
подсистемы до момента замещения находятся
в облегченном режиме и равнонадежны. В
момент переключения
![]() резервная подсистема скачком переходит
режим работы основной подсистемы, то
есть
резервная подсистема скачком переходит
режим работы основной подсистемы, то
есть
![]() ,
,
где x – время.
Видно, что при отказе одного или нескольких элементов расчета надежности у других элементов изменяются характеристики работы, то есть имеет место последействие (зависимость) отказов.
Представим, что рассматриваемая резервированная система состоит из системы с кратностью резервирования m-1 и одной резервной подсистемы. Очевидно, что резервированная система проработает заданное время t без отказа, если система с кратностью резервирования m-1 проработает безотказно это время или эта система откажет в некоторый случайный момент времени:
![]()
и резервная подсистема, являющаяся работоспособной к моменту , безотказно проработает остальное время. Так как эти события являются несовместными, то вероятность безотказной работы системы с m-кратным облегченным резервом
![]() (1)
,
(1)
,
где Рс.m.(t) – вероятность безотказной работы системы с кратностью резервирования m-1 за наработку t.
![]() -
условная вероятность безотказной работы
m-й
резервной подсистемы за наработку t
при условии, что к моменту
система с кратностью резервирования
m-1
отказала.
-
условная вероятность безотказной работы
m-й
резервной подсистемы за наработку t
при условии, что к моменту
система с кратностью резервирования
m-1
отказала.
Так как в рассматриваемой системе имеет место последействие отказов подсистем, то условная вероятность безотказной работы m-й подсистемы за наработку t можно представить в следующем виде
![]() (2)
,
(2)
,
где Рс.0( ) – вероятность работоспособного состояния резервной подсистемы к моменту времени ;
![]()
- вероятность безотказной работы резервной подсистемы на интервале t- при условии, что к моменту отказало m подсистем.
fc.m( ) – плотность вероятности отказа системы с кратностью резервирования m-1 к моменту времени .
Т.к. подсистемы равнонадежные, то вероятность
![]() (3),
(3),
где
![]() - вероятность безотказной работы одной
подсистемы за наработку t-
.
- вероятность безотказной работы одной
подсистемы за наработку t-
.
(2) и (3) в (1)
![]() (4)
(4)
Т.к. наработка до отказа у всех подсистем подчинена экспоненциальному закону надежности, то
![]()
![]()
fc.m(
)
= -![]()
Вначале рассмотрим самый простой случай, когда m=1 (то есть дублирование), тогда плотность вероятности отказа системы с нулевой кратностью резервирования или основной подсистемы:
![]()
Вероятность безотказной работы основной подсистемы
![]()
Подставляя в (4):
![]()
m = 2:
Аналогично
можно получить выражение для Рc.3(t)
и так далее. Тогда в общем случае при
m![]() 1
вероятность безотказной работы системы
с m-кратным
облегченным резервом
1
вероятность безотказной работы системы
с m-кратным
облегченным резервом
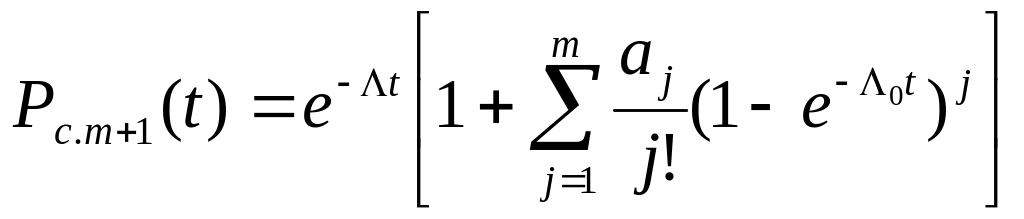 (5),
(5),
где
![]()
Определим среднюю наработку до отказа системы с m-кратным облегченным резервом.
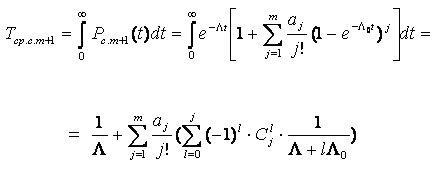
(6),
где
![]() - число сочетаний из j
по l.
- число сочетаний из j
по l.
Если
обозначить
![]() - коэффициент надежности резервной
подсистемы, то после преобразования
(6) получим:
- коэффициент надежности резервной
подсистемы, то после преобразования
(6) получим:
![]() (7)
(7)
Определим выигрыш в надежности средней наработки до отказа, полученный при облегченном резервировании
![]() (8)
(8)
Из формул (5), (7), (8) следует, что показатели надежности и выигрыш в надежности системы с облегченным резервом увеличиваются с увеличением m и уменьшением K0. Величина прироста выигрыша в надежности по средней наработке до отказа уменьшается с увеличением m, так как резервные подсистемы, находясь в облегченном режиме работы, хотя и в меньшей степени, расходуют свой ресурс с момента начала работы системы.
