Часть 2. Определение погрешностей при косвенных измерениях. Вычисление объема и плотности тела
Цель работы: Определение объема и плотности тела методом косвенных измерений. Оценка абсолютной и относительной погрешностей.
Приборы и оборудование: штангенциркуль, технические весы, разновес, измеряемое тело.
Краткая теория
В тех случаях, когда физическая величина не может быть измерена непосредственно, прибегают к косвенным измерениям.
Пусть для нахождения величины N пришлось измерить какие-то величины X, Y, Z. Все величины связаны функциональной зависимостью N = f (x, y, z).
В этом случае средняя абсолютная ошибка <N> может быть найдена по правилам дифференцирования, если значок дифференциала d заменить значком ошибки и выбрать знаки таким образом, чтобы величина ошибки была максимальной, т.е.
,
(7)
.
(8)
Пример 1
Уравнение
свободного падения g
вычисляется по формуле
,
т.е.
.
;
.
В
частном случае, когда N
= f(x),
формула (8) принимает вид
,
т.е. абсолютная ошибка равна абсолютной
ошибке аргумента, умноженной на
производную этой функции.
Относительная погрешность находится по формуле
,
(9)
а так как дифференциал натурального логарифма
, (10)
то
,
или
(11)
таким образом, относительная ошибка результата равна полному дифференциалу натурального логарифма функции, определяющей зависимость данной величины от измеряемых величин. при вычислении надо брать сумму абсолютных значений дифференциалов всех членов логарифма (все частные ошибки складываются) с заменой значков d значком .
Определение погрешностей для косвенных измерений удобно проводить по следующим этапам:
вычисляем относительную ошибку измерения по формуле (9), для этого следует:
прологарифмировать расчетную формулу;
найти от логарифма полный дифференциал;
сгруппировать все члены, содержащие одинаковый дифференциал, и выражения в скобках, стоящие перед дифференциалом, взять по модулю;
заменить все дифференциалы d независимых переменных абсолютными ошибками измерений , а все минусы перед дифференциалом заменить плюсами; так как все частные ошибки складываются.
Пример 2
;
Находим относительную ошибку по пунктам:
а)
;
б)
;
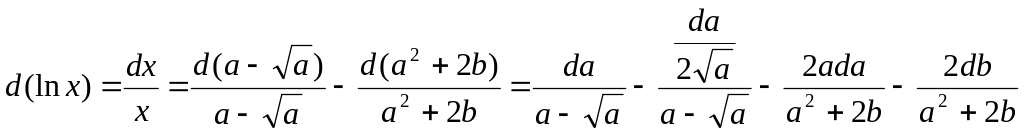в)
г)
.
вычисляем по расчетной формуле (1) средний результат x.
По формуле (9) находим абсолютную ошибку измерения:
.
Окончательное действительное значение величины будет:
.
Вычислительную работу рекомендуется проводить с помощью инженерного калькулятора, производя округления по правилам приближенных чисел. Необходимо твердо помнить, что точность результата определяется точностью измерительных приборов и тщательностью исходных измерений.
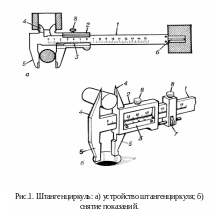
Описание прибора: штангенциркуль предназначен для измерения внутренних и наружных размеров деталей. Конструкции штангенциркулей различных типов могут различаться, однако основные элементы являются общими (рис. 1, а). Штангенциркуль, как и другие штангенинструменты (штангенрейсмас, штангенглубиномер), имеет измерительную штангу (отсюда и название этой группы) с основной шкалой и нониус — вспомогательную шкалу для отсчёта долей делений. Точность его измерения — десятые доли миллиметра.
Штангенциркуль состоит из следующих деталей:
штанга,
подвижная рамка,
шкала нониуса,
губки для внутренних измерений,
губки для наружных измерений,
линейка глубиномера,
винт,
в
инт
для зажима рамки.
Измерения: для определения объема трубки необходимо определить ее геометрические размеры – длину, внешний и внутренний диаметры.
Определение объема: Измерение длины проводят следующим образом. Раздвинув достаточно ножки 5 штангенциркуля, помещают между ними продольно трубку вблизи шкалы. Ножку 5 подводят так, чтобы трубка была слегка зажата, и производят отсчет. Так как ножка 5, а следовательно, и ноль нониуса переместились на длину трубки, то отсчитывают по линейке целое число миллиметров до нуля нониуса и смотрят, какое деление нониуса совпадает с некоторым делением линейки. Измерение проводят несколько раз, повернув перед каждым из них трубку около ее оси на некоторый угол (около 45°). Из всех полученных измерений берут среднее арифметическое.
Далее производят измерение внешнего диаметра трубки (см. рис. 1, б). Измеряют одинаковое количество раз в том и другом конце трубки, слегка зажимая трубку между ножками штангенциркуля и держа ее при этом перпендикулярно к шкале линейки. Из всех измерений берут среднее.
При измерении внутреннего диаметра трубки вводят части ножек 5 штангенциркуля в трубку и разводят их настолько, чтобы они прилегали к внутренним стенкам трубки, и производят отсчет. Потом измеряют другой внутренний диаметр трубки, повернув ее на несколько градусов. Такие же измерения производят на другом конце трубки. Берут среднее значение из всех измерений.
Примечание: Если штангенциркуль не приспособлен специально для измерений внутреннего диаметра трубок, то необходимо принимать во внимание толщину обеих стенок его ножек. Эта толщина указывается на самом штангенциркуле.
По результатам измерений по формулам вычисляют объем трубки методом косвенных измерений.