Исследование затухающих колебаний с помощью пружинного маятника

Вопросы допуска

1. Какие колебания называются гармоническими? График.

2. Какие колебания называются затухающими? График.

3. Что понимают под периодом затухающих колебаний?

4. Как вычисляется период колебаний пружинного маятника?

5. Как экспериментально определить коэффициент жесткости пружины?

6. В чем суть предложенного в работе способа проверки формулы для периода колебаний пружинного маятника?

7. Что называется логарифмическим декрементом затухания и как его определить в случае слабого затухания?

8. Как вычислить показатель затухания и коэффициент сопротивления?

Контрольные вопросы

1. При проверке формулы для периода колебаний пружинного маятника не учитывалось сопротивление среды. Насколько это оправданно?

2. На пружине с коэффициентом жесткости k колеблется гиря массой т. Как изменится период колебаний, если взять гирю большей массы? Если прежней массе укоротить пружину?

3. Выведите формулу для периода колебаний пружинного маятника.

4. Докажите, что при наличии сил сопротивления амплитуда убывает по экспоненциальному закону.

5. Что называют добротностью колеблющейся системы? Как она связана с логарифмическим декрементом?

Литература: [2]; [3]; [4]; [9]; [10], [11].

Ц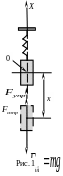 ель работы: 1. Определить коэффициент жесткости пружины и экспериментально проверить формулу периода колебаний пружинного маятника. 2. Определить показатель затухания и логарифмический декремент затухания пружинного маятника. Вычислить коэффициент сопротивления.

Оборудование: пружинный маятник, зеркальная шкала, набор грузов, секундомер.

Краткая теория

Пружинный маятник - механическая колебательная система, состоящая из упругой пружины и подвешенного на ней груза, причем масса пружины намного меньше массы груза (рис. 1). В положении равновесия пружина растянута на величину х₀. Условие равновесия: Выведенный из положения равновесия груз (расстояние х₁) будет двигаться под действием двух сил – силы упругости и силы тяжести, равнодействующая которых где х = х₁+х₀.

Уравнение движения имеет вид:

Исключая вес mg, получим

Величина х означает смещение груза из положения равновесия под действием силы тяжести. Теперь -kx означает равнодействующую сил натяжения пружины и веса груза. Но все это не затрагивает математическую сторону колебательного процесса. Поэтому можно рассуждать так, как если бы силы тяжести совсем не было. [2, 3, 4, 9, 10, 11].

С учетом силы упругости (-kx), силы сопротивления при малых скоростях движения ( ), внешней силы F_вн уравнение движения маятника имеет вид

(2)

1. В случае, когда колебания маятника собственные незатухающие ( 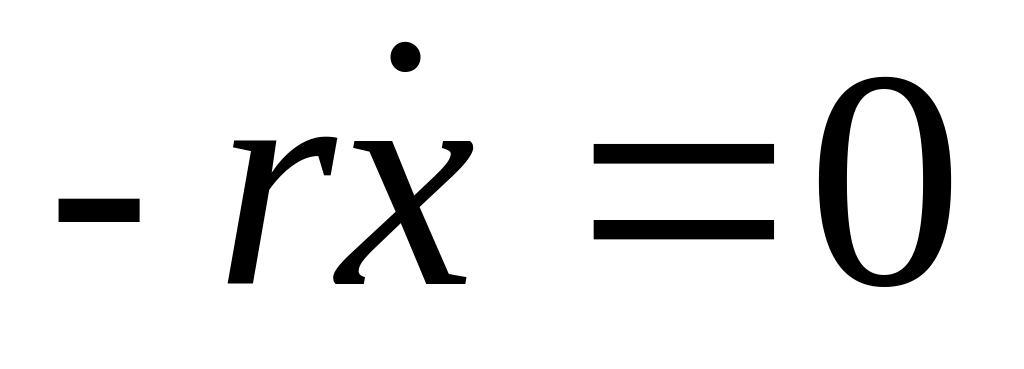, F_вн= 0) уравнение (2) примет вид:

(3)

Обозначим , тогда уравнение (3) принимает вид:

. (4)

Решением такого дифференциального уравнения является гармоническая функция вида [2]; [10], [11]:

, (5)

где А – амплитуда колебаний, аргумент функции (ω₀t + φ₀) – фаза, ее значение (φ₀) в начальный момент времени t = 0 – начальная фаза, ω₀ – собственная угловая частота системы.

(6)

В такой системе возникают незатухающие гармонические колебания, период которых равен:

. (7)

2. Механическая система с трением ( 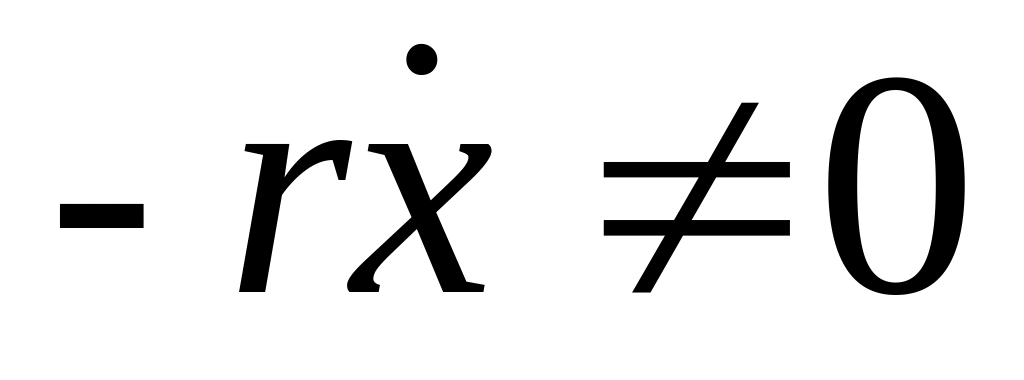, F_вн= 0).

В этом случае колебания маятника называются собственными затухающими.

Дифференциальное уравнение затухающих колебаний имеет вид

(8)

Уравнение (8) можно переписать в удобной для решения форме:

, (9)

где – коэффициент затухания. (10)

Все коэффициенты, входящие в уравнение (9), с достаточной точностью можно считать постоянными. Решение этого уравнения приводит к следующему результату (потери энергии в системе малы δ ≤ ω₀) ([2, 10, 11]):

, (11)

где , - частота и период колебаний системы.

П остоянные величины А, φ₀ - определяются из начальных условий. Амплитуда затухающих колебаний убывает по экспоненциальному закону (см. рис. 2):

. (12)

Для характеристики быстроты затуханий колебаний вводится безразмерная величина Θ – логарифмический декремент затухания, который определяет затухание системы за один период:

, (13)

где , t – время затухания колебаний, n – количество колебаний (n ≥ 10, 50, 70,…). При медленном убывании амплитуды удобнее сравнивать амплитуды не через период, а через n периодов.

В технике часто механические системы характеризуются добротностью Q колебательной системы. Добротностью колебательной системы называют умноженное на π число полных колебаний n, в течение которых амплитуда уменьшается в е раз:

. (14)