Модификация метода Эйлера. Усовершенствованный метод Эйлера.

1. Разобьем отрезок [a, b], на котором требуется найти решение y = y (x) уравнением y′ = f(x, y) на n равных частей точками х_i+1 = х₀ + i · h (i = 0, 1, 2, …, n), где – шаг интегрирования, x₀ = а, x_n = b .

2. Найдём х_i+1/2 = х_i + h/2 .

3. Вычислим вспомогательные значения искомой функции y=y(x) в точке х_i+1/2

y_i+1/2 = y_i + h/2·f(x, y)

4. Находим y_i+1/2 = f (х_i+1/2 , y_i+1/2).

5. Определяем y_i+1/2 = y_i + h·y_i+1/2.

Далее весь процесс вычислений повторяем, начиная с n = 2, до тех пор, пока не будут получены y_i для всех точек х_i (i = 0, 1, 2, …, n) отрезка [a, b].

Пример 5.2. Дана последовательно протекающая реакция вида

Найти время в интервале 120 минут, когда выход С_Р будет максимальным, если при t = 0, С_Р = 0, С_A0 =0,3 моль/дм³.

k₁ = 5·10–2 дм³ · моль^–1 · мин^–1;

k₂ = 7,5·10–3 дм³ · моль^–1 · мин^–1.

Использовать усовершенствованный метод Эйлера.

Сравнить значения, полученные в результате использования метода Эйлера (пример 5.1) и усовершенствованного метода Эйлера.

Решение

1. Разобьем интервал времени 120 минут на 12 интервалов. Определим шаг интегрирования.

– шаг интегрирования, x₀ = 0, x_n = 120 .

2. Найдём по формуле х_i+1/2 = х_i + h/2 значения для i=0.

х_0+1/2 = х₀ + 10/2=5

3. Вычислим вспомогательные значения искомой функции y=y(x) в точке х_0+1/2

y_0+1/2 = y₀ + 10/2·f(x, y),

где (см. пример 5.1) при t=0.

y_0+1/2 = 0 + 10/2·0,015=0,075.

4. Находим y_i+1/2 = f (х_i+1/2 , y_i+1/2).

.

5. Определяем y_i+1/2 = y_i + h·y_i+1/2=0+10·0,0145=0,145.

Заносим результаты вычислений в таблицу.

Выполнение работы.

Расчет 1.

Исходные данные

СА0	k1	k2	число разбиений
0,3	0,05	0,0075	12
моль/дм3	дм3 · моль–1 · мин–1	дм3 · моль–1 · мин–1

y′ = f(xi, yi)0,05·0=,3·е^-0,05·t -0,0075·C_P

Дополнительные расчеты

интервал
а	в	h
0	120	10

В таблицу расчетов (табл.5.3) вносим ссылки на исходные данные.

Таблица 5.3.

Решение уравнения усовершенствованным методом Эйлера. Расчет 2.

i	хi	yi	y′=f(xi,yi)	xi+1/2 = хi+h/2	yi+1/2=yi+ h/2·f(x,y)	y′i+1/2=f(xi+1/2,yi+1/2)	h· y′i+1/2
0	0	0	0,015	5	0,075	0,011682012	0,1168201
1	10	0,116820117	0,008221809	15	0,157929163	0,006209347	0,0620935
2	20	0,178913592	0,00417634	25	0,19979529	0,00295572	0,0295572
3	30	0,208470792	0,001783421	35	0,217387899	0,001043078	0,0104308
4	40	0,218901574	0,000388267	45	0,220842911	-6,07734E-05	-0,000608
5	50	0,21829384	-0,000405929	55	0,216264195	-0,000678286	-0,006783
6	60	0,211510981	-0,000839526	65	0,207313349	-0,001004719	-0,010047
7	70	0,201463788	-0,001058018	75	0,1961737	-0,001158212	-0,011582

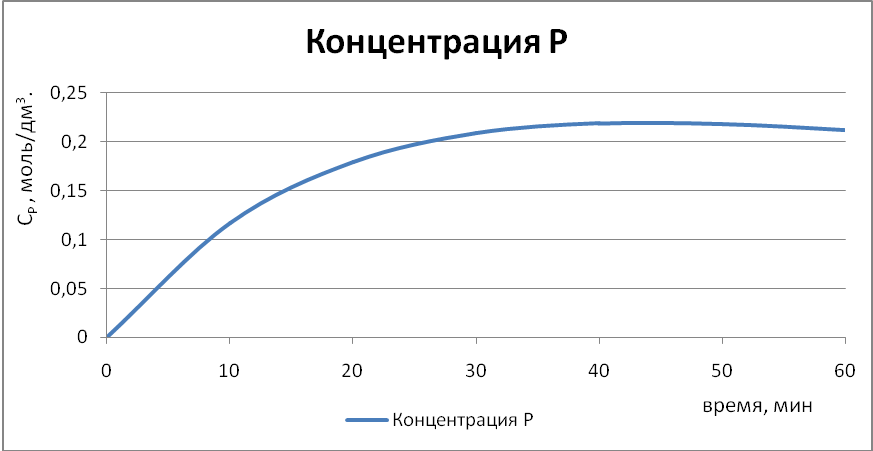
Рисунок 5.2. - Определение максимальной концентрации компонента Р для последовательной реакции по усовершенствованному методу Эйлера. Расчет 1.

Ответ: Время достижения максимальной концентрации компонента Р выражено нечетко. Сузим интервал и повторим расчеты с меньшим шагом.

Расчет 2.

Исходные данные

СА0	k1	k2		число разбиений
0,3	0,05	0,0075		12
моль/дм3	дм3 · моль–1 · мин–1	дм3 · моль–1 · мин–1

y′ = f(xi, yi)0,05·0=,3·е^-0,05·t -0,0075·C_P

Дополнительные расчеты

интервал
а	в	n
40	50	0,8333

В таблицу расчетов (табл.5.4) вносим ссылки на исходные данные.

Таблица 5.4.

Решение уравнения усовершенствованным методом Эйлера. Расчет 2.

i	хi	yi	y′=f(xi,yi)		xi+1/2 = хi+h/2		yi+1/2=yi+ h/2·f(x,y)	y′i+1/2=f(xi+1/2,yi+1/2)	h· y′i+1/2
0	40	0,2189016		0,000388267		40,416667	0,2190634	0,000346413	0,000288677
1	40,83333	0,2191903		0,000303256		41,25	0,2193166	0,000263109	0,000219258
2	41,66667	0,2194095		0,000222146		42,083333	0,2195021	0,000183638	0,000153031
3	42,5	0,2195625		0,000144775		42,916667	0,2196229	0,000107839	8,98656E-05
4	43,33333	0,2196524		7,09896E-05		43,75	0,219682	3,55603E-05	2,96336E-05
5	44,16667	0,219682		6,39237E-07		44,583333	0,2196823	-3,33442E-05	-2,77868E-05
6	45	0,2196543		-6,64185E-05		45,416667	0,2196266	-9,90151E-05	-8,25125E-05
7	45,83333	0,2195717		-0,000130321		46,25	0,2195174	-0,000161587	-0,000134656
8	46,66667	0,2194371		-0,000191199		47,083333	0,2193574	-0,000221189	-0,000184324
9	47,5	0,2192528		-0,000249178		47,916667	0,2191489	-0,000277945	-0,000231621
10	48,33333	0,2190211		-0,000304381		48,75	0,2188943	-0,000331973	-0,000276644
11	49,16667	0,2187445		-0,000356922		49,583333	0,2185958	-0,000383388	-0,00031949
12	50	0,218425		-0,000406913		50,416667	0,2182555	-0,000432299	-0,000360249

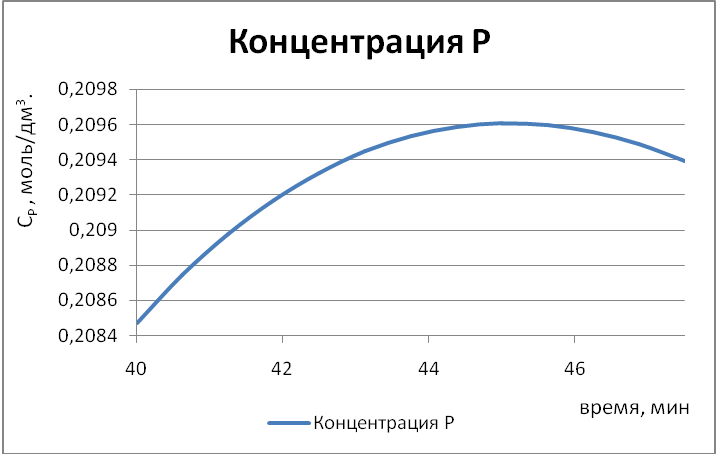
Рисунок 5.2. - Определение максимальной концентрации компонента Р для последовательной реакции по усовершенствованному методу Эйлера. Расчет 2.

Ответ: Максимальная концентрации компонента Р 0,220 моль/дм³ достигается на 45,583 минуте.

Метод Рунге – Кутта.

Последовательность вычислений по методу Рунге – Кутта следующая:

1. Разобьем отрезок [a, b], на n равных частей точками х_i = х₀ + i · h (i = 0, 1, 2, …, n), где , x₀ = а, x_n = b .

2. Находим для каждого i (i = 0, 1, 2, …, n) значения

3. Вычисляем

4. Определяем последовательность значений y_i (i = 0, 1, 2, …, n) искомой функции y = y (x):

y_i+1 = y_i + ∆ y_i

Для выполнения вычислений по методу Рунге – Кутта удобно пользоваться следующей схемой.

i	х	y	y′ = f(x , y)	k = h · f(x , y)	∆ y
0	х0	y0	f(x0 , y0)	ki(0)	k1(0)
	х0 + h/2	y0 + k1(0)/2	f(x0 + h/2, y0 + k1(0)/2)	k2(0)	2·k2(0)
	х0 + h/2	y0 + k2(0)/2	f(x0 + h/2, y0 + k2(0)/2)	k3(0)	2·k3(0)
	х0 + h	y0 + k3(0)	f(x0 + h , y0 + k3(0))	k4(0)	k4(0)
					0
1	х1	y = y0 + ∆y0	f(x1 , y0)	k1(1)	k1(1)
	х1 + h/2	y1 + k1(1)/2	f(x1 + h/2, y1 + k1(1)/2)	k2(1)	2·k2(1)
	х1 + h/2	y1 + k2(1)/2	f(x1 + h/2, y1 + k2(1)/2)	k3(1)	2·k3(1)
	х1 + h	y1 + k3(1)	f(x1 + h , y1 + k3(1))	k4(1)	k4(1)
2	х2	y2 = y1 + ∆y1

Метод Рунге – Кутта является одним из методов повышенной точности и, несмотря на его трудоёмкость, широко используется при численном решении дифференциальных уравнений и систем обыкновенных дифференциальных уравнений.

Пример 3. Решим уравнений (1) с начальным условием y(0) = 0 на отрезке [0 , 3] с шагом h = 1.

Интегрирование дифференциального уравнения методом Рунге – Кутта.

i	х	y	y′ = f(x , y)	k = h · f(x , y)	∆ y
0	0	0	0,05	0,05	0,05
	0,5	0,025	0,0486	0,0486	0,0972
	0,5	0,0243	0,0486	0,0486	0,0972
	1,0	0,0486	0,0473	0,0473	0,0473
					0,0486
1	1,0	0,0486	0,0473	0,0473	0,0473
	1,5	0,0722	0,0459	0,0459	0,0818
	1,5	0,0716	0,0459	0,0459	0,0818
	2,0	0,0945	0,0446	0,0446	0,0446
					0,0459
2	2,0	0,0945	0,0446	0,0446	0,0446
	2,5	0,1168	0,0433	0,0433	0,0966
	2,5	0,1161	0,0433	0,0433	0,0866
	3,0	0,1378	0,0421	0,0421	0,0421
					0,0433
3	3,0	0,1378

Ход работы:

1. Получить индивидуальное задание для расчёта кинетических кривых последовательной реакции первого порядка (С_А нач., k₁, k₂, время протекания реакции).

2. Выполнить расчёт по приведённым схемам.

3. Построить кинетические кривые в Excel или Word.

4. Сделать вывод о точности методов.

5. Оформить отчёт в Word ( А – 5 ).