§2. Основные показатели динамики.

Для количественной оценки динамики социально-правовых явлений применяются такие статистические показатели как абсолютные приросты, темпы роста, темпы прироста, которые делятся на базисные, цепные и средние. В основе расчета этих показателей динамики лежит сравнение уровней ряда динамики. Если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения, то эти показатели называются базисными. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень с которого начинается какой-то новый этап развития явления (например, число осужденных по статьям УК РФ с 1997 года – года вступления в силу нового Уголовного кодекса). Если сравнение осуществляется при переменной базе, и каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные таким образом показатели динамики называются цепными.

Для рядов динамики со значительными колебаниями уровней в качестве базы сравнения применяются средние уровни.

Абсолютный прирост (Δу) равен разности двух сравниваемых уровней.

Базисный абсолютный прирост

Δy_t^б=y_t-y_б.

Цепной абсолютный прирост

Δy_t=y_t - y_t-1.

Средний абсолютный прирост

где y_t - уровень сравниваемого периода;

y_t-1 - уровень предшествующего периода;

y_б - уровень базисного периода;

y₁,y_n – первый и последний уровни ряда соответственно;

n - число уровней ряда.

Темп роста (Т ) - это отношение уровня ряда одного периода к уровню ряда другого периода, выраженное в процентах.

Базисный темп роста T_t^б=

Цепной темп роста T_t=

Средний темп роста

_{Замечание. Если темп роста и средний темп роста вычисляются в долях (не умножаются на 100%), то они называются соответственно коэффициентом роста и средним коэффициентом роста.}

Темп прироста (Т_пр)вычисляется как отношение абсолютного прироста (Δу) к уровню, принятому за базу сравнения. Темп прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Он может быть положительным, отрицательным или равным нулю.

Базисный темп прироста Т_{пр t}^б=

Цепной темп прироста Т_{пр t}=

_{Средний темп прироста}

_{Замечание. Если вычислен соответствующий темп роста, то темп прироста равен:}

_{Тпр.=Тр.-100 (%).}

Сведем выражения для вычисления указанных выше показателей в таблицу:

Таблица 17.

Основные показатели динамики

показатель	Абсолютный прирост	Темп роста	Темп прироста
базисный	Δytб=yt-yб	Ttб=	Тпр tб=
цепной	Δyt=yt-yt-1	Tt=	Тпр t=
средний

_{Пример. Рассчитать абсолютные приросты, темпы роста и темпы прироста числа осужденных за взяточничество базисным и цепным способом, используя данные таблицы 9. За базу взять 2004 год.}

_{Решение. Используя приведенные выше формулы, получим:}

Базисный абсолютный прирост

Δy^б₂₀₀₂=y₂₀₀₂-y₂₀₀₄=2035-2930= - 895_, Δy^б₂₀₀₃=y₂₀₀₃-y₂₀₀₄=2232-2930= - 698,

Δy^б₂₀₀₅=y₂₀₀₅-y₂₀₀₄=3609-2930=679_, Δy^б₂₀₀₆=y₂₀₀₆-y₂₀₀₄=4229-2930=1299_.

Цепной абсолютный прирост

Δy₂₀₀₃=y₂₀₀₃-y₂₀₀₂=2232-2035=197_, Δy₂₀₀₄=y₂₀₀₄-y₂₀₀₃=2930-2232=698_,

Δy₂₀₀₅=y₂₀₀₅-y₂₀₀₄=3609-2930=679 _, Δy₂₀₀₆=y₂₀₀₆-y₂₀₀₅=4229-3609=620_.

Средний абсолютный прирост

Базисный темп роста

T^б₂₀₀₂= T^б₂₀₀₃= T^б₂₀₀₅= T^б₂₀₀₆=

Цепной темп роста

T₂₀₀₃=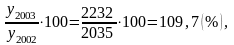 T₂₀₀₄=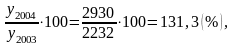

T₂₀₀₅= T₂₀₀₆=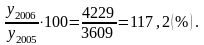

Средний темп роста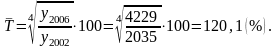

Базисный темп прироста

Т_пр^б₂₀₀₂= Т_пр^б₂₀₀₃=

Т_пр ^б₂₀₀₅=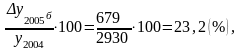 Т_пр^б₂₀₀₆=

Цепной темп прироста

Т_пр2003= Т_{пр 2004}=

Т_{пр 2005}= Т_пр2006=

Средний темп прироста

Наряду с указанными показателями в ряду динамики может быть рассчитан средний уровень ряда. Он применим для любого ряда динамики: интервального и моментного.

В интервальных рядах динамики средний уровень ряда ( ) определяется делением суммы уровней ряда на их число, т. е. по методу средней арифметической:

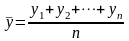
где y₁,y₂,…,y_n - значения уровней ряда; n - число уровней.

Пример. Рассчитать средний уровень ряда числа осужденных за взяточничество, используя данные таблицы 9.

Решение. Используя приведенную выше формулу для интервального ряда динамики, получим:

В моментных рядах для вычисления среднего уровня ряда применяется средняя хронологическая – средняя, вычисленная по значениям, изменяющимися во времени.

В моментном ряду с равными интервалами времени средний уровень - средняя хронологическая моментного ряда - определяется по формуле:

где y₁,y₂,…,y_n - значения уровней ряда; n - число уровней.

Пример. Сведения о численности контингента исправительной колонии представлены в таблице:

год	По состоянию на 1 января
	2004	2005	2006	2007	2008	2009
Численность контингента	518	553	540	580	468	525

Найти среднегодовую численность контингента исправительной колонии.

Решение. Как видно из условия задачи, мы имеем моментный ряд с равными интервалами, т.к. численность контингента приводится на начало каждого года, а число дней в году будем считать одинаковым (наличие високосных 2004 и 2008 гг. не оказывает существенного влияния на вычисление среднегодовой численности). Значит, среднегодовая численность контингента исправительной колонии равна:

В моментном ряду с неравными интервалами времени средний уровень ряда определяется по формуле средней хронологической взвешенной:

где y₁,y₂,…,y_n - значения уровней ряда; n - число уровней; t₁,t₂, … t_n-1 – длительность интервалов времени между уровнями.

Пример. Определить среднегодовую численность лиц с мерой пресечения в виде заключения под стражей в следственном изоляторе по данным, приведенным в таблице:

Дата	1.01	1.04	1.07	1.09	1.01
Количество человек	102	120	121	117	120

Решение. Мы имеем моментный ряд с неравными интервалами, где средний уровень ряда определяется по формуле средней хронологической взвешенной.

Из условия задачи следует:

y₁=102, t₁=31+28+31=90; y₂=120, t₂=30+31+30=91; y₃=121, t₃=31+31=62;

y₄=117, t₄=30+31+30+31=122; y₅=120.

Тогда среднегодовая численность лиц с мерой пресечения в виде заключения под стражей в следственном изоляторе равна:

Пример. За сентябрь 2009 года в списочной численности сотрудников УВД города произошли следующие изменения:

• на 1.09.09 числилось 200 человек;

• принято на работу: 5.09.09 – 3 чел., 24.09.09 – 7 человек;

• уволилось: 10.09.09 – 5 человек, 20.09.09 – 3 чел.

Определить среднюю списочную численность сотрудников УВД в сентябре 2009 г.

Решение. В данном случае мы имеем моментный ряд с неравными интервалами, где средний уровень ряда определяется по формуле средней хронологической взвешенной.

Из условия задачи следует, что:

с 1 сентября по 4 сентября у₁=200 чел., t₁=4;

с 5 сентября по 9 сентября у₂=203 чел., t₂ =5;

с 10 сентября по 19 сентября у₃=198 чел., t₃=10;

с 20 сентября по 23 сентября у₄=195 чел., t₄=4;

с 24 сентября у₅=202 чел.

Тогда средняя списочная численность сотрудников УВД в сентябре 2009 г. равна: