1.3 Погрешность результатов арифметических операций и элементарных функций

Почти всегда искомая величина y зависит от параметров а₁, a₂, ..., a_N, которые по своей природе являются приближенными числами. Возникает задача отыскания погрешности функции y=F(а₁, a₂, ...,a_N ) по известным погрешностям а_к., k=1…N.

Своеобразие приближенных чисел состоит в том, что их значения нельзя рассматривать как постоянные – они могут меняться в пределах их абсолютных погрешностей: а_к = х_к  _к . Эта особенность позволяет применить к приближенным числам понятия дифференциального исчисления.

Пусть х_к – истинные значения некоторых чисел, а а_к – их приближенные значения.

Абсолютная погрешность функции тогда

C другой стороны, разлагая в ряд Тейлора, имеем

.

Тогда

где

Отсюда следует оценка где

в области

Часто пользуются линейной оценкой погрешности:

.

Выражение для относительной погрешности имеет вид

.

Проведем конкретную оценку для простейших функций.

1. Сложение. .

.

Видно, что относительная погрешность суммы не превосходит наибольшей относительной погрешности слагаемых.

2. Вычитание. ; a_k > 0.

Абсолютная погрешность при вычитании равна сумме абсолютных погрешностей уменьшаемого и вычитаемого. Видно, что относительная погрешность при вычитании близких чисел может быть весьма велика (а₁ – а₂ – мало). Поэтому на практике всегда следует избегать вычитания близких чисел, при необходимости преобразовывая выражения. Неприятности могут случиться даже в простых случаях, что иллюстрирует приведенная ниже таблица 1.1. Число , взятое с разной степенью точности, использовано для расчета выражения и равносильных ему. Результаты могут ошеломить неподготовленного человека!

Таблица 1.1 – Вычитание близких чисел

2	7/5=1,4	17/12=1,41(6)	1,414	1,4142	1,41421356
(2–1)6	0,004096	0,005233	0,00503503	0,00504964	0,005050633883
(3–22)3	0,008	0,004630	0,00500045	0,00505303	0,005050633883
(52–7)2	0	0,0069(4)	0,00490	0,0050410	0,005050633883
99–702	1	–0,1(6)	0,020	0,0060	0,005050633883

3. Умножение.

Относительная погрешность произведения равна сумме относительных погрешностей сомножителей.

4. Деление.

Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя.

5. Степень. ( m – const).

Относительная погрешность степени равна относительной погрешности основания, умноженного на показатель.

6. Логарифм.

Абсолютная погрешность натурального логарифма равна относительной погрешности аргумента.

1.4 Обратная задача теории погрешности

Обратная задача состоит в том, что требуется определить погрешность аргументов таким образом, чтобы обеспечить заданную погрешность функции.

Вообще-то эта задача математически неопределена, так как заданную погрешность _у функции у=F(a₁, a₂,...,a_N ) можно обеспечить, по-разному устанавливая погрешности ее аргументов. Приведем простейшее решение этой задачи [1], используя принцип равных влияний, то есть, предполагая, что все слагаемые в формуле одинаково влияют на образование погрешности функции: т.е. Тогда и

Следовательно,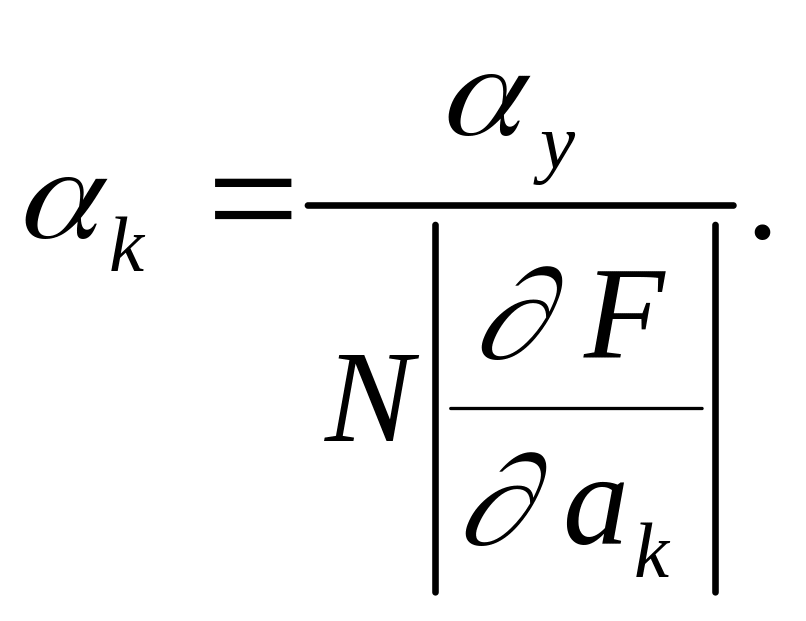

Аналогично,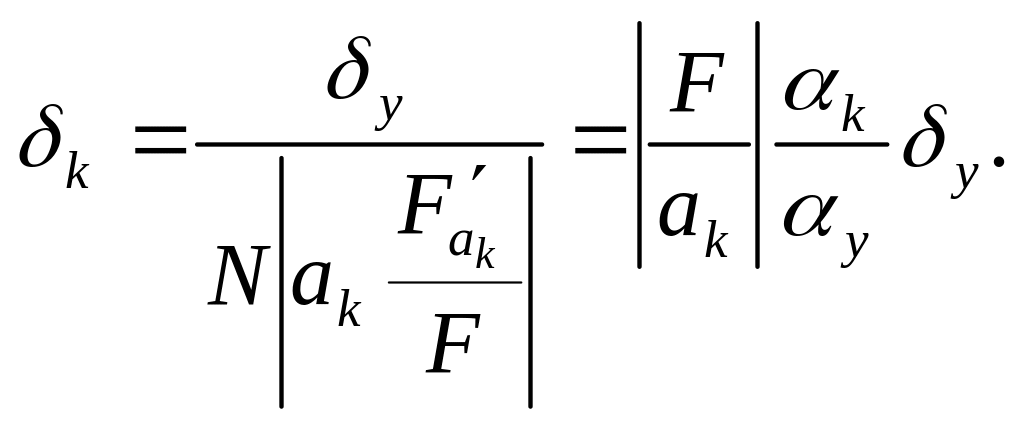

1 Оператор (отображение) - закон, по которому каждому элементу х некоторого множества Х сопоставляется однозначно определенный элемент y другого заданного множества Y

1 Погрешность - отклонение приближенного решения задачи от истинного