10.Линия тока, трубка тока, траектория

• В потоке жидкости можно выделить воображаемую линию, в каждой точке которой вектор скорости в данный момент времени направлен по касательной к ней (рисунок 3.2). Такая линия называется линией тока. Совокупность линий тока образуют поверхность, и если эта поверхность замкнутая, то она называется трубкой тока. Трубка тока малого сечения s (в пределе ds ) называется элементарной струйкой. Т.к. в каждой точке линии тока и поверхности трубки тока нормальная составляющая скорости равна нулю, то через линию тока и через поверхность трубки тока нет перетекания, а линии тока не пересекаются. Поэтому количество жидкости, протекающей между двумя линиями тока, одинаково, и там, где линии тока сближаются, скорости увеличиваются, и наоборот; количество жидкости, протекающей в пределах трубки тока одинаково, и если сечение трубки переменное, то и скорость также переменна.

Рисунок 3.2 Линия и трубка тока

В общем случае через одну точку можно провести только одну линию тока, но существуют некоторые особые точки, в которых это правило нарушается. Такие точки являются критическими, когда при обтекании непроницаемой поверхности величина скорости становится равной нулю (точки А и А, рисунок 3.3,а), а также источники (стоки), когда скорость становится равной бесконечности при вытекании жидкости из одной точки или ее втекании в одну точку (рисунок 3.3,б).

• 

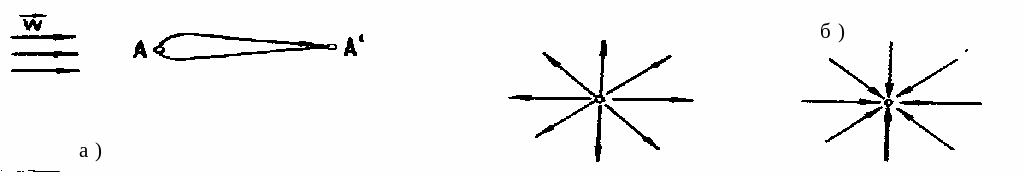
  Рисунок 3.3 Особые точки

  

  a)

  б)

  Рисунок 3.5. Линии тока и траектории

  Если рассматривать движение частиц во времени, то линия, по которой она двигалась в некотором промежутке времени, называется траекторией. При стационарном движении линии тока остаются неподвижными относительно системы отсчета, и в этом случае они представляют собой траектории движущихся частиц. При нестационарном движении частицы не будут оставаться на тех же линиях тока, а следовательно линии тока и траектории не совпадают. В момент t₁векторы скорости частиц a, b, c лежат на линии тока (рис. 17а); и частица a в моменты t₂ и t₃ не будет повторять положение частиц b и с на линии тока, траектория частицы a отклонится от линии тока в момент t₁. Это положение удобно проиллюстрировать на примере, изображенном на рис. 17б. Если подачу жидкости в резервуар отрегулировать таким образом, чтобы уровень Н₁ был неизменным, то истечение струи из отверстия будет стационарным, а траектория частицы совпадать с линией тока (линия t₁). Если же подачу жидкости в резервуар прекратить, то истечение жидкости при переменном уровне нестационарное; линии тока в моменты времени t₁, t₂, t₃ изображены сплошными линиями, а траектория частицы М  пунктирной.

• Уравнение линии тока. Если элементарный вектор dr  перемещение частицы за время dt (рис. 3.5), то скорость

• 

В декартовых координатах

• 

а

• ,

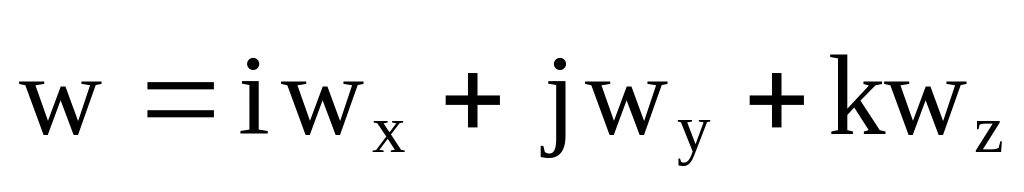где

• 

откуда

• 

Следовательно

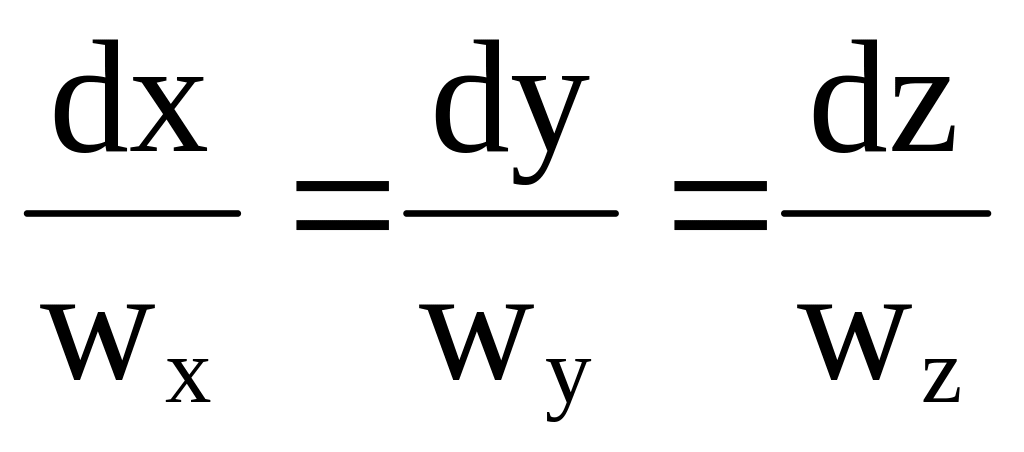• , (3.10)

или система уравнений линии тока в декартовых координатах имеет вид:

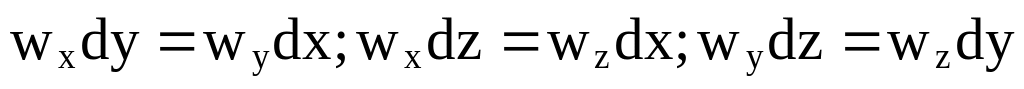• . (3.11)

• Поток вектора скорости  это интеграл по поверхности s (рис. 15) от произведения вектора скорости на нормаль к этой поверхности (или от проекции скорости на нормаль) в каждой точке, т.е.

• 

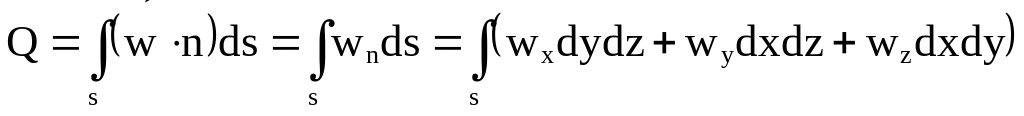
Поток вектора скорости физически представляет собой секундный объемный расход жидкости через поверхность s. Размерность потока вектора скорости [Q]=[w][s]=м³/с. Если поверхность s замкнута, то при отсутствии внутри поверхности источников и стоков поток вектора скорости будет равен нулю

• .

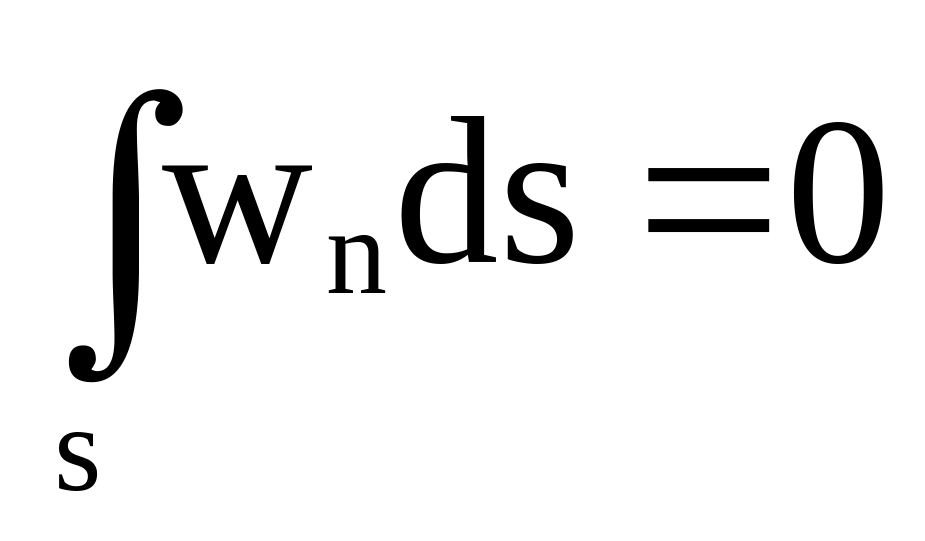При наличии источников

• 

при наличии стоков

•